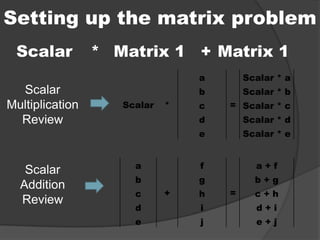
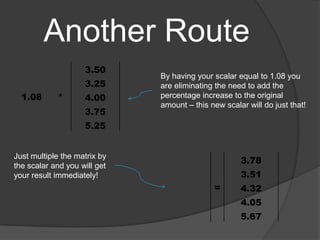
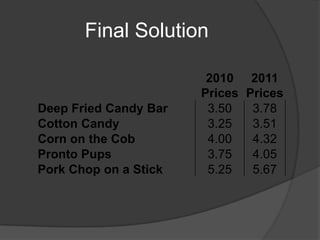
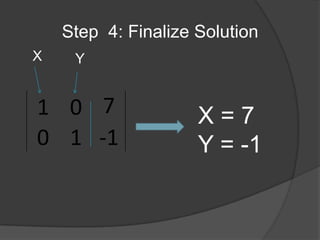
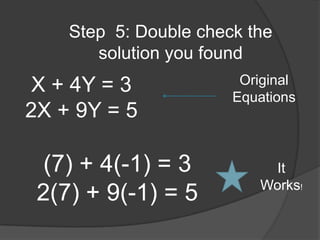
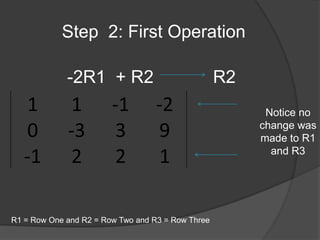
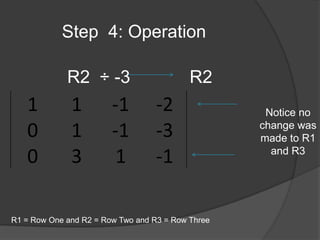
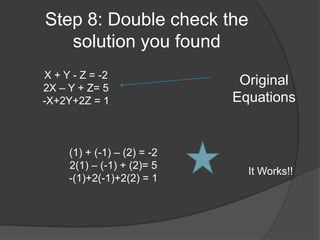
The document provides information and steps to solve multiple math word problems using systems of linear equations and matrices. It discusses using row operations to transform matrices into reduced row echelon form to solve systems of linear equations with 1, 2, and 3 variables. It also sets up and solves a word problem using a matrix to determine unknown prices from collected revenue and item quantities sold at two gates.

1. Question OneIt is 2011 and the Minnesota State Fair is just around the corner. Ryan can’t wait to go and stand in line for all of his favorite state fair foods. He always make sure that he stops at the following booths: Deep Fried Candy Bar $3.50, Cotton Candy $3.25, Corn on the Cob $4.00, Pronto Pup $3.75, and the Pork Chop on a Stick $5.25. Ryan heard from Lena that all the food booths at the state fair are increasing their prices by 7%. If this is the case how much will he now have to pay for all of his favorite foods?

2. Helpful AdviceFor this problem using scalar multiplication would be a very useful tool.

3. Step 1: Make a Matrix

4. Setting up the matrix problemScalar Multiplication Review Scalar Addition Review

5. Run the numbers

6. Another Route By having your scalar equal to 1.08 you are eliminating the need to add the percentage increase to the original amount – this new scalar will do just that! Just multiple the matrix by the scalar and you will get your result immediately!

7. Final Solution

8. Question TwoSolve the following system of linear equations. X + 4Y = 32X + 9Y = 5

9. NotationRow switching : A row within the matrix can be switched with another row. R1 R2 Row multiplication: Each element in a row can be multiplied by a non-zero constant.k* R1 R1, k ≠ 0Row addition: A row can be replaced by the sum of that row and a multiple of another row. R1 + kR2 R1, k ≠ 0

10. The ultimate goal is to get our matrix to look like the one to the left and then the values in the #1, #2 locations will be the solutions to the problemfor x and yGoal

11. Using row operations here we go….Step 1: Set up the augmented matrix Step 2: First Operation

12. Step 2: First Operation -2R1 + R2 R2Notice no change was made to R1 (row 1)R1 = Row One and R2 = Row Two

13. Step 3: Second Operation -4R2 + R1 R1Notice no change was made to R2 (row 2)R1 = Row One and R2 = Row Two

14. Step 4: Finalize SolutionXYX = 7 Y = -1

15. Step 5: Double check the solution you foundX + 4Y = 32X + 9Y = 5Original Equations(7) + 4(-1) = 32(7) + 9(-1) = 5It Works!

16. Question ThreeSolve the following system of linear equations. X + Y - Z = -22X – Y + Z= 5-X+2Y+2Z = 1Same idea but now we have to work with the three variables.

17. The ultimate goal is to get our matrix to look like the one to the left and then the values in the #1, #2, #3 locations will be the solutions to the problemfor x and y and z Goal

18. Using row operations here we go….Step 1: Set up the augmented matrix

19. Step 2: First Operation -2R1 + R2 R2Notice no change was made to R1 and R3 R1 = Row One and R2 = Row Two and R3 = Row Three

20. Step 3: Operation R1 + R3 R3Notice no change was made to R1 and R2 R1 = Row One and R2 = Row Two and R3 = Row Three

21. Step 4: Operation R2 ÷ -3 R2Notice no change was made to R1 and R3 R1 = Row One and R2 = Row Two and R3 = Row Three

22. Step 5: Operation -3R2 + R3 R3Notice no change was made to R1 and R2 R1 = Row One and R2 = Row Two and R3 = Row Three

23. Step 6: Operation R3 ÷ 4 R3Notice no change was made to R1 and R2 R1 = Row One and R2 = Row Two and R3 = Row Three

24. Step 7: Finalize Solution Now:X + Y - Z = -2Y - Z= -3Z = 2Then:Lastly:X + Y - Z = -2X + (-1) – 2 = -2X-3 = -2X= 1 Y - Z = -3Y - 2= -3Y = -1

25. Step 8: Double check the solution you foundX + Y - Z = -22X – Y + Z= 5-X+2Y+2Z = 1Original Equations(1) + (-1) – (2) = -22(1) – (-1) + (2)= 5-(1)+2(-1)+2(2) = 1It Works!!

26. Question FourNow to wrap it all up we want to determine how much it actually costs to get into the fair and enjoy this fun get together! As you saw on the clip, one day at the fair just isn’t enough!! At the gates on opening day they are selling one day passes as well as bonus three day passes. We were only able to collect the data for 2 particular gates on this day. Gate A sells 2,090 day passes and 980 three day passes. Gate B sells 1,807 day passes and 712 three day passes. If Gate A collected $31,290 and Gate B collected $24,753, how much does it cost to by a one day pass and a three day pass?

27. Helpful AdviceFor this problem finding the determinate and the inverse would be a very useful tool.

28. Set up a Matrix Matrix FormatMatrix specific to this example

29. Finding the determinant

30. Finding the inverse of a matrix

32. Double check the solutions to make sure they do indeed work in the problem

33. Final Solution In the future you can go to this Excel document to plug in your matrix information and have it automatically calculate