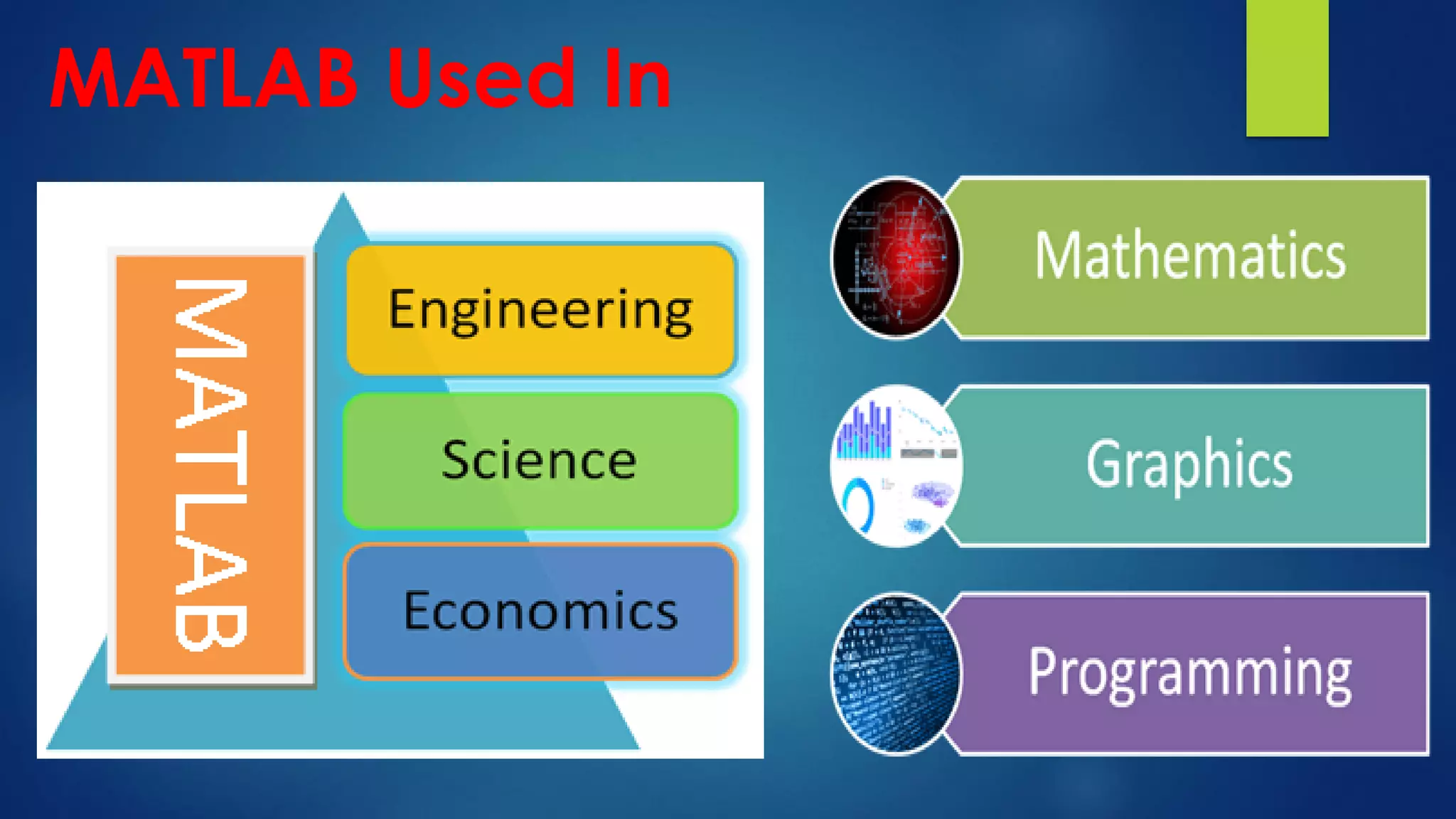
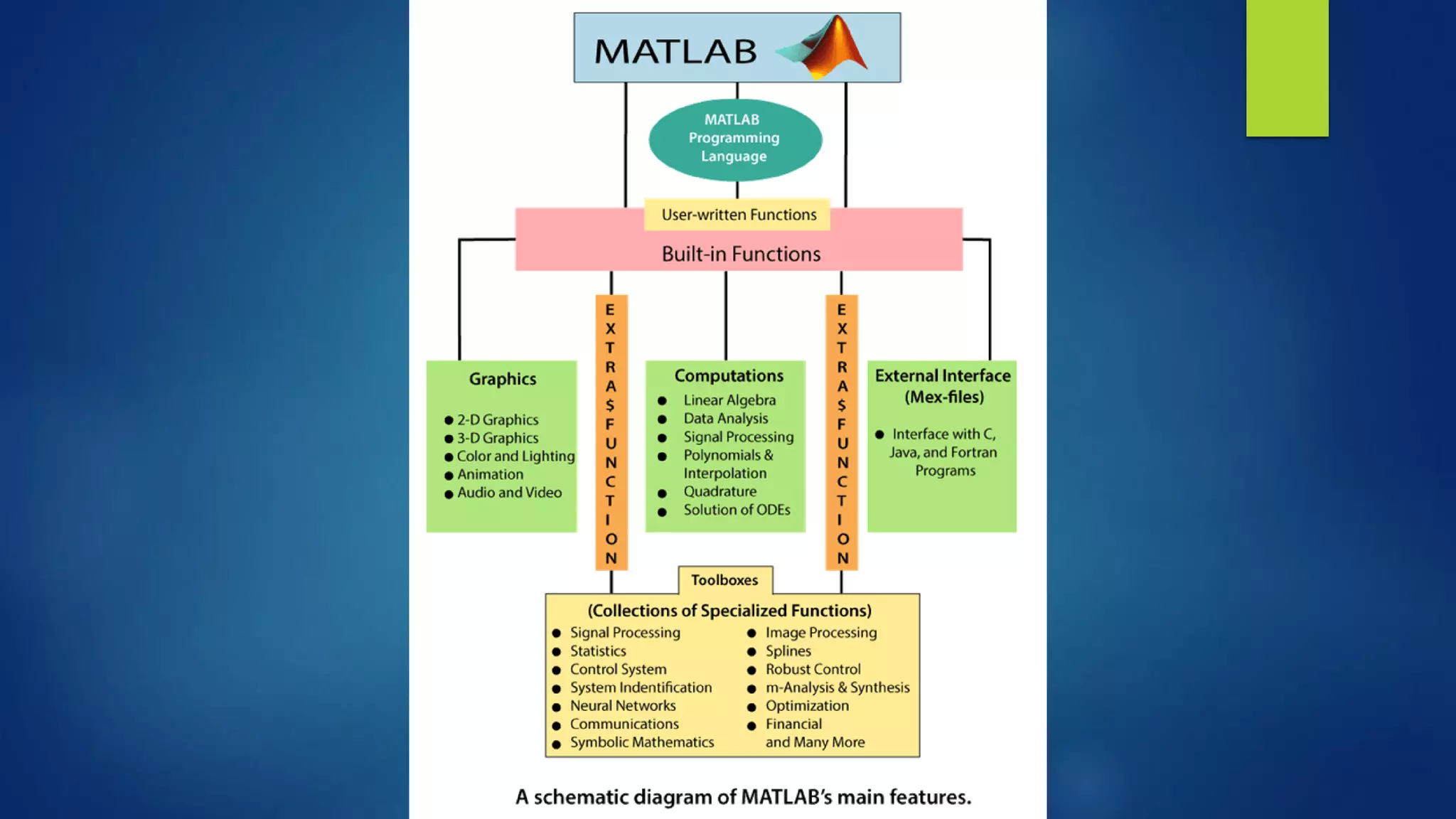
This document provides an overview of MATLAB, including what it is, its features, toolboxes, applications, and how to perform various tasks. MATLAB is a numerical computing environment and programming language used for algorithm development, data analysis, and visualization. It allows matrix operations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs in other languages. The document describes MATLAB's various components, data types, commands, and how to work with matrices, arrays, plots, and other mathematical functions. It also outlines uses of MATLAB in domains like signal processing, control systems, image processing, and more.

1. GOVIND SATI

2. Outlook
 Introduction to MATLAB
 What is MATLAB
 MATLAB Use
 Features of MATLAB
 Toolboxes
 MATLAB System
 Applied MATLAB
 industrial MATLAB
 MATLAB Learning Platform
 MATLAB Environment
 Type of Files in MATLAB
 MATLAB Commands
 Data Types in MATLAB
 MATLAB Array
 Application of MATLAB
 MATLAB Plotting
 Linear Algebra
 Symbolic Mathematics
 Polynomial Functions
 MATLAB Control System
 MATLAB Application in DSP
 Digital Filter Design
 MATLAB Simulink

3. Introduction to MATLAB
 In 1970 Mr Moloer wrote MATLAB, which is referred as “MATrix LABoratory”.
 It is a software package used to perform scientific computations and visualization.
 MATLAB has the ability:-
• Variable management
• Data import and export
• Calculation based on matrix
• Generates plots and graphs

4. What is MATLAB
 MATLAB is a software package for high – performance mathematical
computation, visualization, and programming environment.
 MATLAB is a fourth generation programming language which provide
 numerical computing environment,
 data visualization,
 data analysis and
 algorithm development feature.
 MATLAB stands for Matrix Laboratory.

5. MATLAB Used In

6. Features of MATLAB
 High level language for technical computing.
 Development environment for manage code, files, data visualization.
 Mathematical function for linear algebra, statistics, Fourier analysis.
 Provide interfaces to work with other programming languages such as C,
C++, Java, .NET, Python, SQL, Hadoop.
 MATLAB Toolboxes for other application.

8. Graphics
•2-D
•3-D
•Color and
Lighting
•Animation
•Audio and
Video
Computations
•Linear Algebra
•Data Analysis
•Signal
Processing
•Polynomials
•Quadrature
•Solution of
ODEs
External
Interface
•Interface with
C, Java and
Fortran
Programs

9. Toolboxes
 Signal Processing
 Statistics
 Control System
 System Identification
 Neural Networks
 Communications
 Symbolic Mathematics
 Image Processing
 Aerospace
 Robust Control
 M-Analysis & Synthesis
 Optimization
 Arduino
 Financial and Many More

10. Applied MATLAB
 Computational Biology
 Control Systems
 Data Science
 Deep Learning
 Machine Learning
 Wireless Communications
 Image Processing
 Computer Vision
 IOT
 Embedded Systems
 Test and Measurement
 Mixed Signal Systems
 Power Electronics Control Design
 Predictive Maintenance
 Robotics
 Signal Processing
 Mechatronics
 Enterprise and IT Systems

11. Industrial MATLAB
 Communications
 Earth, Ocean and Atmospheric
Sciences
 Biological Sciences
 Biotech and Pharmaceutical
 Quantitative Finance and Risk
Management
 Energy Production
 Metals Materials and Mining
 Industrial Automation and
Machinery
 Aerospace and Defence
 Neuroscience
 Software and Internet
 Electronics
 Medical Devices
 Semiconductors
 Automotive
 Railway Systems

12. MATLAB Learning Platform
 MATLAB Software
 MATLAB Mobile
 MATLAB Online
 Octave Offline
 Octave Online

13. MATLAB Software

14. MATLAB Mobile

15. MATLAB Online

16. MATLAB Octave

17. MATLAB Environment
 The major components of the MATLAB environment are
 Command Window
 Command History
 Workspace
 Current Directory
 Figure Window
 Edit Window

18. Types of Files in MATLAB
 There are three different types of files in the MATLAB:
1. M- files, 2. MAT-files, 3.MEX-files
1. M-files
M-files are standard ASCII text files, with a (.m) extension to the filename. Any program written
in a MATLAB editor is saved as M-files. These files are further classified as
 Script Files
An M-file with a set of valid MATLAB commands is called a script.
 Function Files
An M-files which begins with a functions definition line is called a function file. If a file does not
begin with function definition line, it becomes a script file.

19. output
input
function name
for statement block
function
keyword
help lines
for function
Make sure you save changes to the
m-file before you call the function!
Scripts & Function

20.  2. MAT-file
MAT-files are binary data-files, with an (.mat) extension to the filename. These are created
by MATLAB when data is saved using save command. The save command saves data form
the current MATLAB workspace into a disk file.
save <filename>
To load the data saved in the MAT-file, the load command is used.
load <filename>
 3. MEX – file
 MEX-file is MATLAB callable FORTRAN and C program, with a (.mex) extension. This
feature allows the user to integrate the code written in FORTRAN and C language into
the programs developed using MATLAB.

21. Useful MATLAB Commands
 clc- Clears Screen
 clf- Clears Figure Window
 clear all – Clears the variables in the workspace
 clear xyz – Clears the variables specified in the command
 Ctrl-c – Stops execution of function/command being run currently
 quit / exit - quit MATLAB
 real(x) – Real part of given complex number
 imag(x) – Imaginary part of complex number
 factorial – Gives factorial of a number
 log – Gives natural logarithm
 sqrt – Square root of a number

22. Data Types in MATLAB
 MATLAB provides a user-friendly notation for input and output data. Following are some
data types in MATLAB.
1. Integers :- 1, 2, 3, and -1, -2, -3.
2. Floating:- 3.14159, 2.1456
3. Complex:- 3+4i, 4+2i
4. Constant:- there are several pre-defined constants in MATLAB. Pi, Inf, -Inf, i,j.
5. Text String
6. Vectors
7. Matrices
8. Boolean
9. Arrays

23. MATLAB Array
 An array is a collection of data values organized into rows and columns.
 When the array has only one dimension (either a row or a column), it is known as a vector.
 While a two or more dimensional array is known as a matrix.
A = [1 2 3 4 5] %A is a vector
B = [1 2 3; 4 5 6; 7 8 9] % B is a matrix
C = ‘Hello’ % C is a string array

24. Operators
 MATLAB operators can be classified mainly onto three categories:
1. Arithmetic Operators
(like addition, multiplication, division etc.)
2. Relational Operators
(like less than, not equal to, equal to etc.)
3. Logical Operators
(like AND, OR, NOT etc.)

25. Scalars:-
 A scalars is a (1x1) matrix containing a single element only.
 A scalar does not need any square brackets
P = 10
Vectors:-
 Vectors are two type 1)- Row vector and 2) Column vector
 All the elements of a row vector are separated by blank space or commas and are
enclosed in square brackets.
 All the elements of a column are separated by semicolon.
Q = [1,2,3] / [1 2 3] – row
P = [1; 2; 3] - column
Vectors and Matrices

26. Creating Special Matrices
 ones
A = ones(2,4) % creates a 2x4 matrix
A = ones(3) % creates a 3x3 matrix
 zeros
B = zeros(3) % creates a 3x3 matrix
 eye
C = eye(3) % creates a 3x3 matrix
 rand / randn
D = rand(2,4) % creates a 2x4 matrix
 magic
E = magic(3) % creates a 3x3 matrix

27. Arithmetic Operations on Matrix
 A + B is valid if A and B are matrices of the same size.
 A-B is valid if A and B are matrices of the same size.
 A*B is valid if number of columns of A is equal to number of rows of B.
 A/B is valid if A and B are of the same size and it is equal to AB^-1 for same
size square matrix A and B.
 A^2 is valid if A is square and it equals A*A.
 A^p effectively multiplies matrix A itself (p-1) times.
 If a matrix equation is given by Ax = B, then the command x = AB will give
x = A^-1*B.

28. Arithmetic Operations on Arrays
 Arithmetic Operations on arrays are done on elements-by-elements basis.
 (+) = addition
 (-) = subtraction
 (.*) = element-by-element multiplication
 (./) = element-by-element right division
 (.^) = element-by-element power
 (.) = element-by-element left division

29. MATLAB Plotting
 Plotting is a graphical representation of a data set that shows a
relationship between two or more variables.
 MATLAB plots play an essential role in the field of mathematics,
science, engineering, technology and finance for statistics and
data analysis.
 There are several functions available in MATLAB to create 2-D
and 3-D plots.

30. 2-D Plots
 MATLAB plot()
 MATLAB fplot()
 MATLAB Semilogx()
 MATLAB Semilogy()
 MATLAB loglog()
 MATLAB polar()
 MATLAB fill()
 MATLAB bar()
 MATLAB barh()
 MATLAB plotyy()
 MATLAB area()
 MATLAB pie()
 MATLAB hist()
 MATLAB stem()
 MATLAB stairs()

31. 2-D
 MATLAB provides plotting capability with polar coordinates:
polar(theta, r)
 Example
r=2sin5t,0≤t≤2π

32. 3-D Plots
 MATLAB plot3()
 MATLAB pie3()
 MATLAB fill3()
 MATLAB contour3()
 MATLAB surf()
 MATLAB surfc()
 MATLAB mesh()
 MATLAB meshz()
 MATLAB waterfall()
 MATLAB stem3()
 MATLAB ribbon()
 MATLAB sphere()
 MATLAB ellipsoid()
 MATLAB cylinder()
 MATLAB slice()

33. 3-D
 MATLAB Surface
surf(x,y,z)
Example
x = -5 to 5, y = -5 to 5,
z = cos x cos y e (-√(x^2+y^2 ))/4

34. Linear Algebra
 A linear algebra equation is an equation of the system.
 Express the algebraic equations in matrix form, Ax = B. and find the value of
x.
3x + 4y + z = 2
-2x + 3z = 1
1x +2y + 4z = 0
 AX = B,
 X = B/A = inv(A)*B.
 X = AB

35. MATLAB Polynomial
 Polynomial Evaluation
 Roots of Polynomial
 Polynomial Addition
 Polynomial Subtraction
 Polynomial Multiplication
 Polynomial Division
 Polynomial Differentiation
 Polynomial Integration

36. Polynomial Functions
 MATLAB performs polynomial operations.
P(x) = x4 + 7x3 - 5x + 9
 Solution of this equation at 1, 9, 19 ,21 etc.
P = [1 7 0 -5 9]
x = 1
polycal(P,x)

37.  Laplace
 Inverse Laplace
 Zeros, Poles , Pole-Zeros Map,
 State Space Representation
 Serial / Cascade, Parallel and Feedback Connections
 Step Response
 Impulse Response
 Root Locus Plots
 Bode Plots
 Nyquist Plots
MATLAB Control System

38. Laplace
 Find the Laplace Transform of the function
f(t) =e^-t(1-sin(t))
 Solution
The following command are used.
syms t
ft = exp(-t)*(1-sin(t));
fs = laplace(ft);
The result of the commands is as follows
fs = 1/(1+s)- 1/(2+2*s+s^2)

39.  Inverse Laplace
 Find the Inverse Laplace Transform of the function F(s) = 1/(s+4)
Solution
The following command are used
syms s t
fs = 1/(s+4);
ft = ilaplace(fs)
The results of the command is
ft = exp(-4*t)
Inverse Laplace

40. MATLAB Applications in DSP
 Signal Processing
 Signals Classification
 Representation of Discrete Signals
 Signals Operation
 Addition
 Multiplication
 Scaling
 Folding
 Multi-rate Signal Processing Functions
 Fourier Transform
 Digital Filter Design
 IIR Digital Filter Design
 Filter Design and Analysis Tool

41. Signals Processing
 Signal Processing
(a) Analog or Continuous Time Approach
(b) Digital or Discrete Time Approach
 Discrete Signals Representation
(a) Graphical Representation
(b) Functional Representation
(c) Tabular Representation
(d) Sequential Representation

42. Graphical Representation
 A signal can be graphically represented using stem command
in MATLAB.
 The syntax is given as:
stem(x)
stem(t,x)
stem(t,x, ‘fill’)
stem(t,x, ‘fill’, ‘----’ )
stem(t,x, ‘marker’)

43.  Plot the sine wave in discrete signal form.
𝑡 = −𝜋 𝑡𝑜 𝜋, 𝑦 = sin(𝑡)
Solution:-
t = linspace(-pi, pi, 10);
y = sin(t);
stem(t, y)
Using other command
t = linspace(-pi, pi, 10);
y = sin(t);
stem(t, y, ‘fill’, ‘--’);
title(‘plot of sine wave’);
xlabel(‘discrete time’);
ylabel(‘sine wave amplitude’);

44. Digital Filter Design
 The digital filters can be classified as:
Finite-duration impulse response (FIR) filter
Infinite-duration impulse response (IIR) filter
IIR Digital Filter Design
The different types of IIR digital filters are:
 Butterworth filter
 Chebyshev Type I filter
 Chebyshev Type II filter
 Elliptic filter

45. Filter Design and Analysis Tool
 The Different types of responses that can be viewed are listed
below.
 Magnitude response
 Phase response
 Group delay
 Phase delay
 Impulse response
 Step response
 Pole-zero plot
 Zero-phase plot

46. MATLAB Simulink
 Simulink Modeling
 Wireless Communication
 Power Electronics Control Design
 Control Systems
 Signal Processing
 Robotics
 Advanced Driver Assistance Systems
 Image Processing and Computer Vision
 Etc.