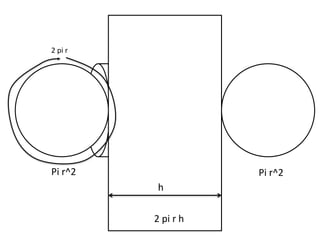
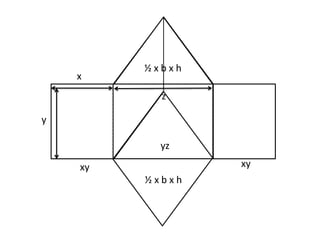
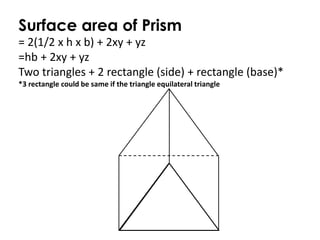
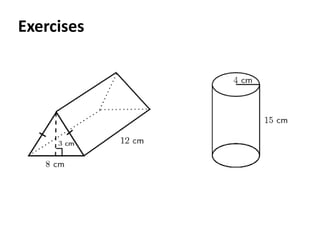
The document discusses the key properties of cylinders and triangular prisms in geometry. It defines cylinders as having a circular base and height, with their volume calculated as pi * r^2 * height. Triangular prisms are defined as having a triangular base, height, and volume calculated as (1/2 * base * height) * height. The surface areas of both shapes are described as consisting of the base areas plus the areas of the additional rectangular sides. Similarities between cylinders and prisms are that their volumes are both calculated as base times height.

1. Tan Wen Hao
Darshiini Vig
Yvonne Tan
Welson Lum
Kong Zhen Chung
Mathematics (MTH 30104)

2. Cylinder & Prism
Cylinder Triangular Prism

3. Cylinder
The base, B
Height, h
Base is a circle,
Area of circle =
pi r*2
Where r is the radius of
the circle
r

4. Volume of Cylinder
=Base x Height
=pi r^2h

5. Pi r^2 Pi r^2
2 pi r h
h
2 pi r

6. Surface area of Cylinder
= 2 (pi r^2) + 2 pi rh
(top and bottom circle + rectangle)

7. Prism
In geometry, a prism is a polyhedron with an n-sided polygonal base, another
congruent parallel base (with the same rotational orientation), and n other faces
(necessarily all parallelograms) joining corresponding sides of the two bases.
The base, B
Height, h

8. Base is a triangle,
Area of triangle =
1/2 x b x h
Where b is the base of
triangle, h is the height.
h
b

9. Volume of Prism (Triangular)
=Base x Height
=(1/2 x b x h) x H

10. ½ x b x h
½ x b x h
x
y
xy xy
z
yz

11. Surface area of Prism
= 2(1/2 x h x b) + 2xy + yz
=hb + 2xy + yz
Two triangles + 2 rectangle (side) + rectangle (base)*
*3 rectangle could be same if the triangle equilateral triangle

12. Similarity between cylinder
and prism
• Both volume are base x height where a
cylinder is a circle-based shaped, prism is
triangular base.*
• Both have identical bases. (top=bottom)

13. Exercises