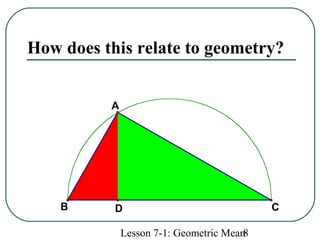
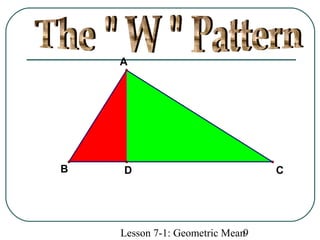
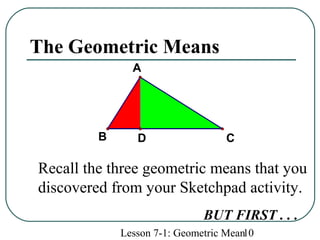
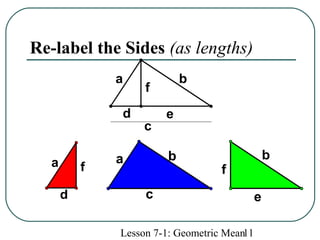
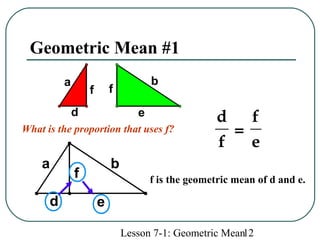
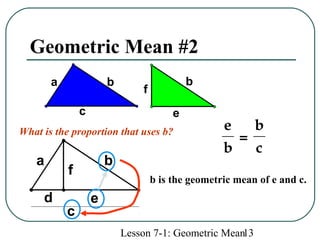
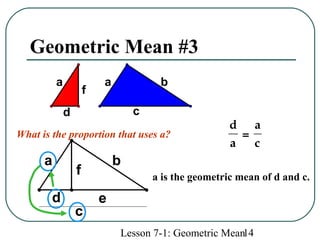
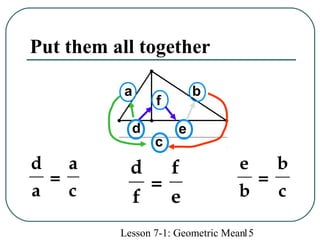
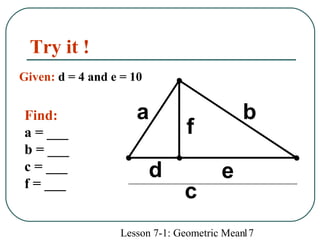
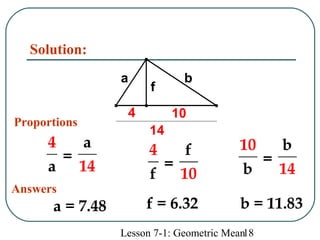
The document defines geometric sequences as patterns of numbers where each term is determined by multiplying the previous term by a common factor. It provides examples of geometric sequences and explains how to find the geometric mean between two terms of a geometric sequence by setting up a proportion. The geometric mean of two numbers a and b is the number x such that a/x = x/b. It also relates the geometric mean to proportions in a geometric figure with three lengths, where each mean length is the geometric mean of the other two lengths in that proportion.

1. Lesson 7-1: Geometric Mean1
Geometric Mean
Lesson 7-1

2. Lesson 7-1: Geometric Mean2
Sequences
Is a pattern of numbers where any term (number in the sequence) is
determined by adding or subtracting the previous term by a
constant called the common difference.
Arithmetic Sequence:
Geometric Sequence:
Is a pattern of numbers where any term (number in the sequence) is
determined by multiplying the previous term by a common factor.
Example: 2, 5, 8, 11, 14, ____, ____, ____17 20 23 Common difference = 3
Example: 2, 6, 18, 54, 162, _____, _____, ____486 1458 4374 Common Factor = 3

3. Lesson 7-1: Geometric Mean3
Examples
1. Starting with the number 1 and using a factor of 4, create 5 terms of
a geometric sequence. 1 , 4 , 16 , 64 , 256
2. Starting with the number 2 and using a factor of 5, create 5 terms
of a geometric sequence. 2 , 10 , 50 , 250 , 1250
3. Starting with the number 5 and using a factor of 3, create 5 terms
of a geometric sequence. 5 , 15 , 45 , 135 , 405
4. In the geometric sequence 2, ____, 72, 432, .Find the missing term.12
5. In the geometric sequence 6, ____, 24,... Find the missing term.12

4. Lesson 7-1: Geometric Mean4
Geometric Mean
A term between two terms of a geometric sequence is the
geometric mean of the two terms.
Example:
Find the geometric mean of 3 and 300.
In the geometric sequence 4, 20, 100, ….(with a factor
of 5), 20 is the geometric mean of 4 and 100.
Try It:
3 , ___ , 30030

5. Lesson 7-1: Geometric Mean5
Geometric Mean : Fact
Consecutive terms of a geometric sequence are proportional.
Example:Consider the geometric sequence with a common factor 10.
4 , 40 , 400
4
40
=
40
400
cross-products are equal
(4)(400) = (40)(40)
1600 = 1600

6. Lesson 7-1: Geometric Mean6
Therefore ………..
To find the geometric mean between 7 and 28 ...
7 , ___ , 28label the missing term x
write a proportion
cross multiply
solve
7
X
=
X
28
X
X2 = (7)(28) X2 = 196
X2 = 196 X = 14

7. Lesson 7-1: Geometric Mean7
a x
x b
=
ab
The geometric mean between two numbers a and b is the
positive number x where . Therefore x = .
Try It: Find the geometric mean of . . .
1. 10 and 40 Answer = 20
2. 1 and 36 Answer = 6
3. 10 and 20 Answer = 14.14
4. 5 and 6 Answer = 5.48
5. 8.1 and 12.2 Answer = 9.94

8. Lesson 7-1: Geometric Mean8
How does this relate to geometry?
D CB
A

9. Lesson 7-1: Geometric Mean9
D CB
A

10. Lesson 7-1: Geometric Mean10
The Geometric Means
D CB
A
Recall the three geometric means that you
discovered from your Sketchpad activity.
BUT FIRST . . .

11. Lesson 7-1: Geometric Mean11
Re-label the Sides (as lengths)
a f
d
ba
c e
f
b
a b
f
d e
c

12. Lesson 7-1: Geometric Mean12
a b
f
d e
Geometric Mean #1
a
f
d e
f
b
d
f
=
f
e
f is the geometric mean of d and e.
What is the proportion that uses f?

13. Lesson 7-1: Geometric Mean13
Geometric Mean #2
ba
c e
f
b
a b
f
d e
c
e
b
=
b
c
b is the geometric mean of e and c.
What is the proportion that uses b?

14. Lesson 7-1: Geometric Mean14
Geometric Mean #3
d
a
=
a
c
ba
c
a
f
d
a b
f
d e
c
a is the geometric mean of d and c.
What is the proportion that uses a?

15. Lesson 7-1: Geometric Mean15
Put them all together
a b
f
d e
c
d
a
=
a
c
e
b
=
b
c
d
f
=
f
e

16. Lesson 7-1: Geometric Mean16
The “W” Pattern
a b
f
d e
c
W

17. Lesson 7-1: Geometric Mean17
Try it !
a b
f
d e
c
Given: d = 4 and e = 10
Find:
a = ___
b = ___
c = ___
f = ___

18. Lesson 7-1: Geometric Mean18
Solution:
4
f
=
f
10
4
a
=
a
14
10
b
=
b
14
a b
f
4 10
14
a = 7.48 f = 6.32 b = 11.83
Proportions
Answers