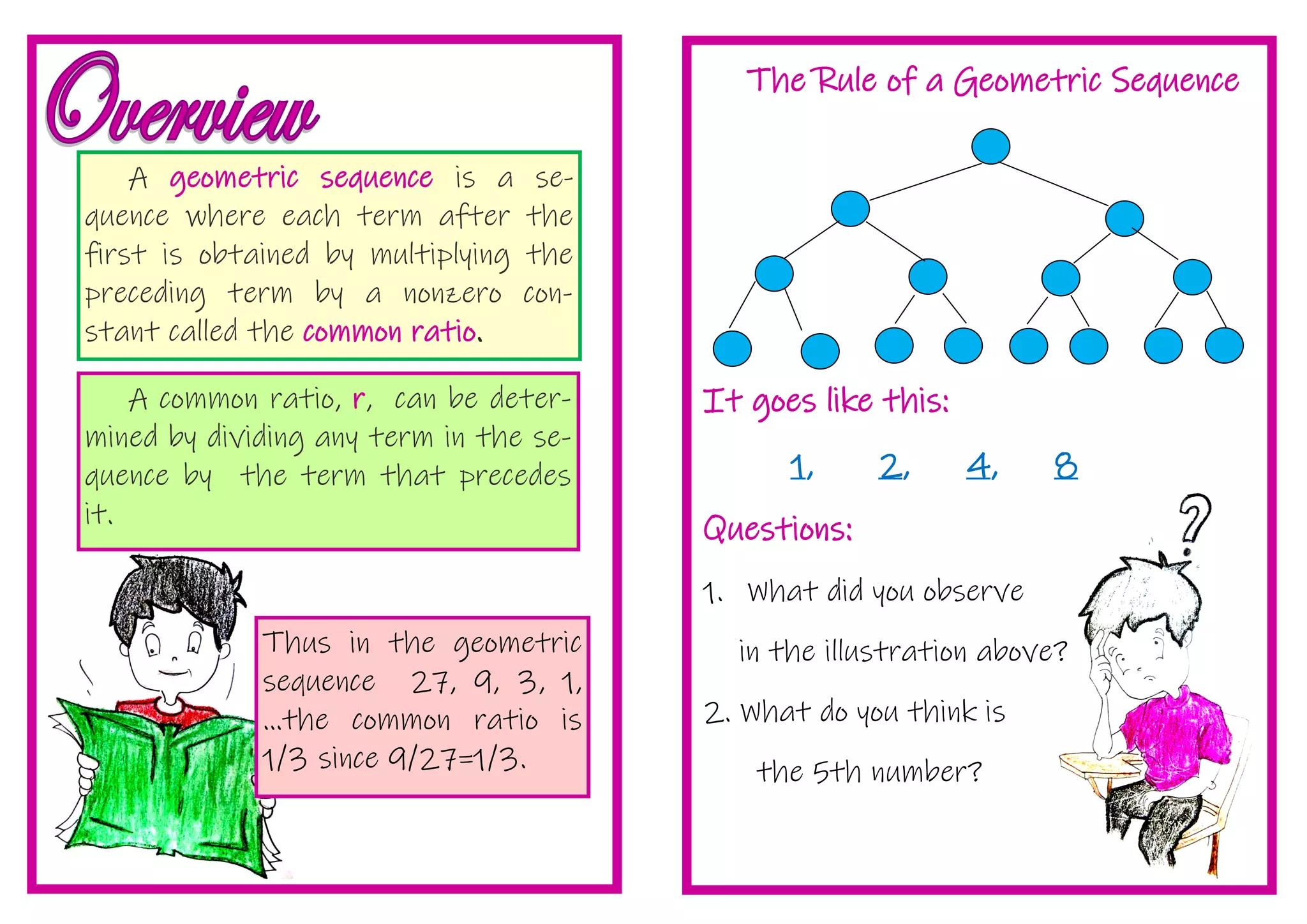
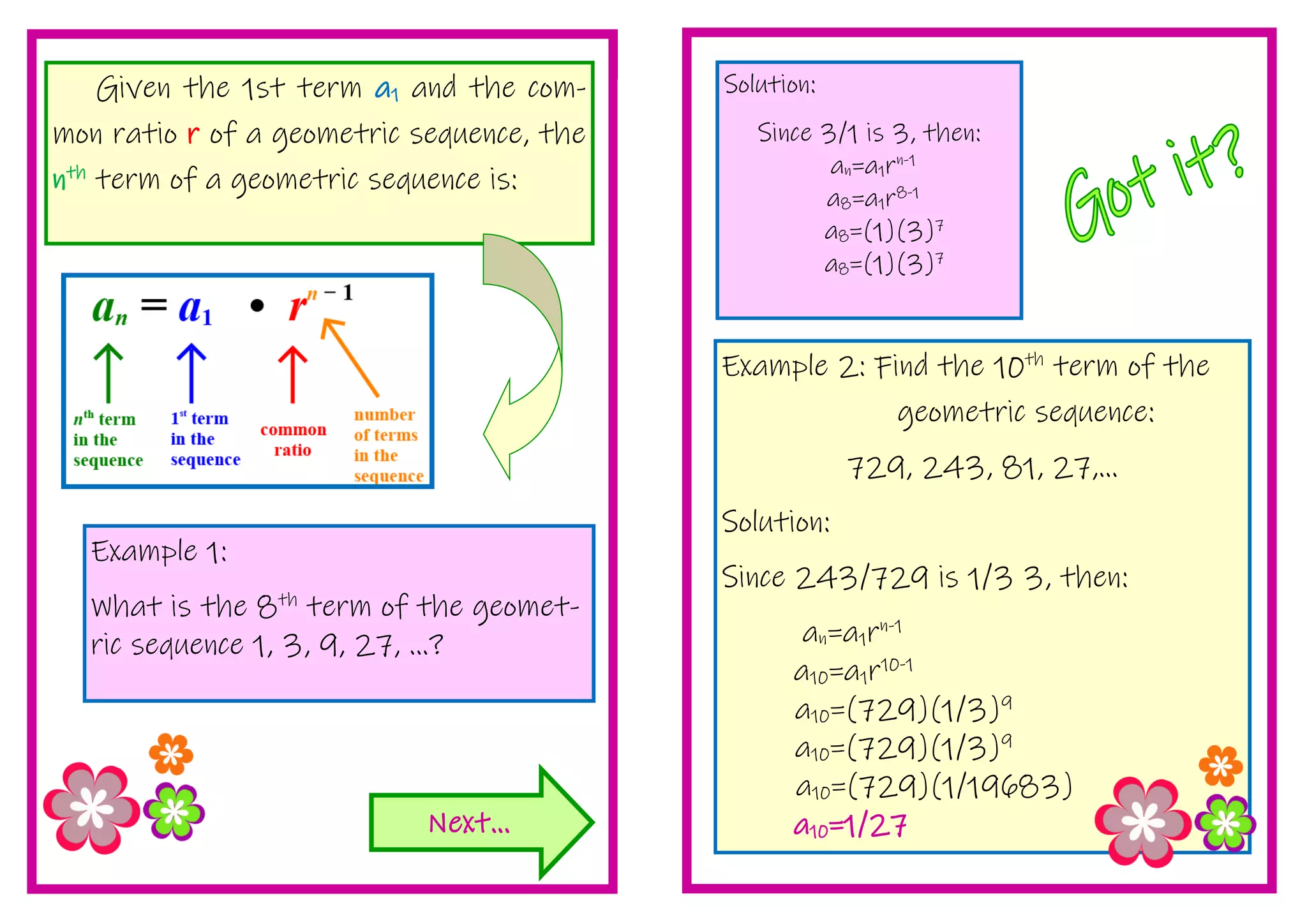
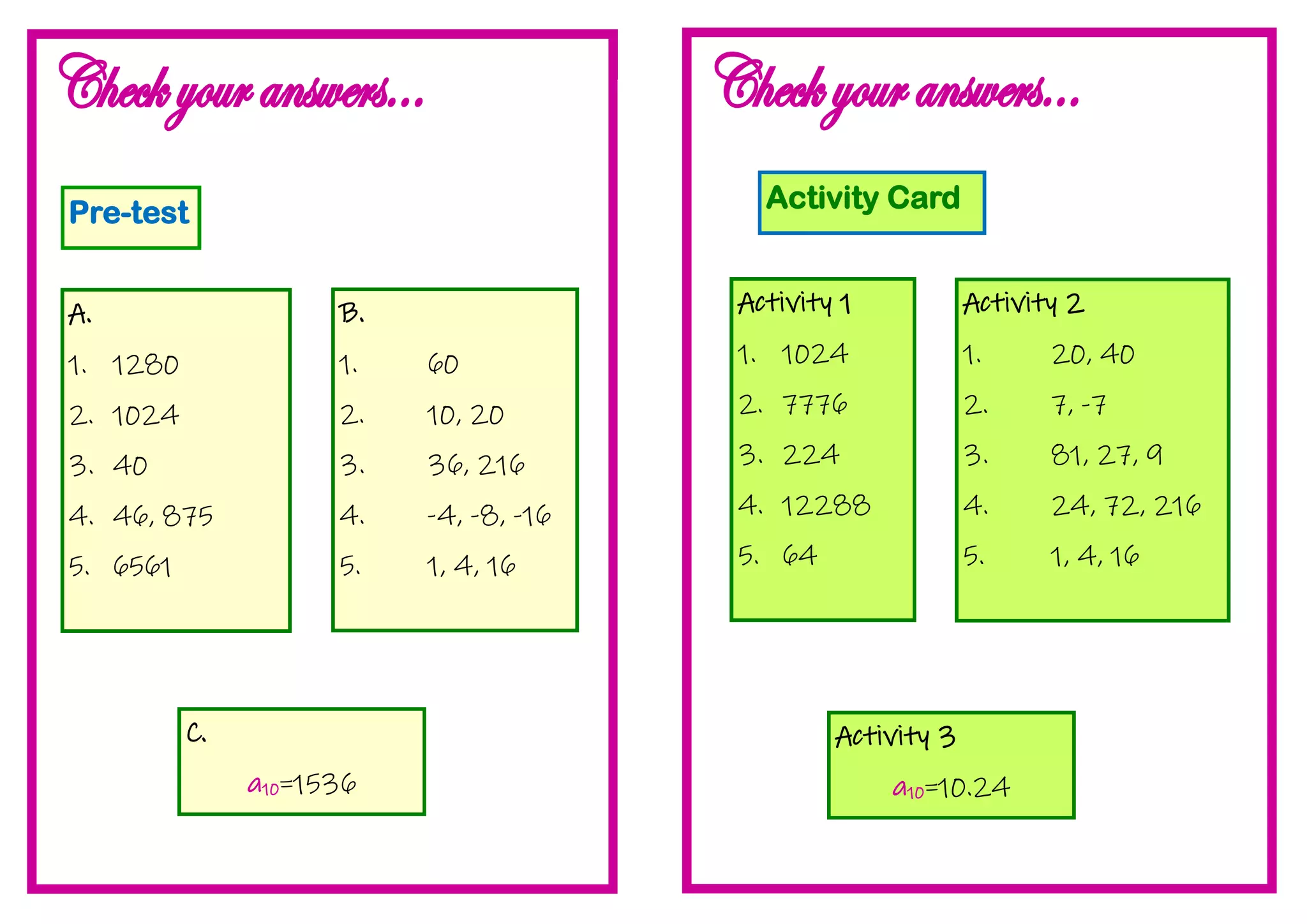
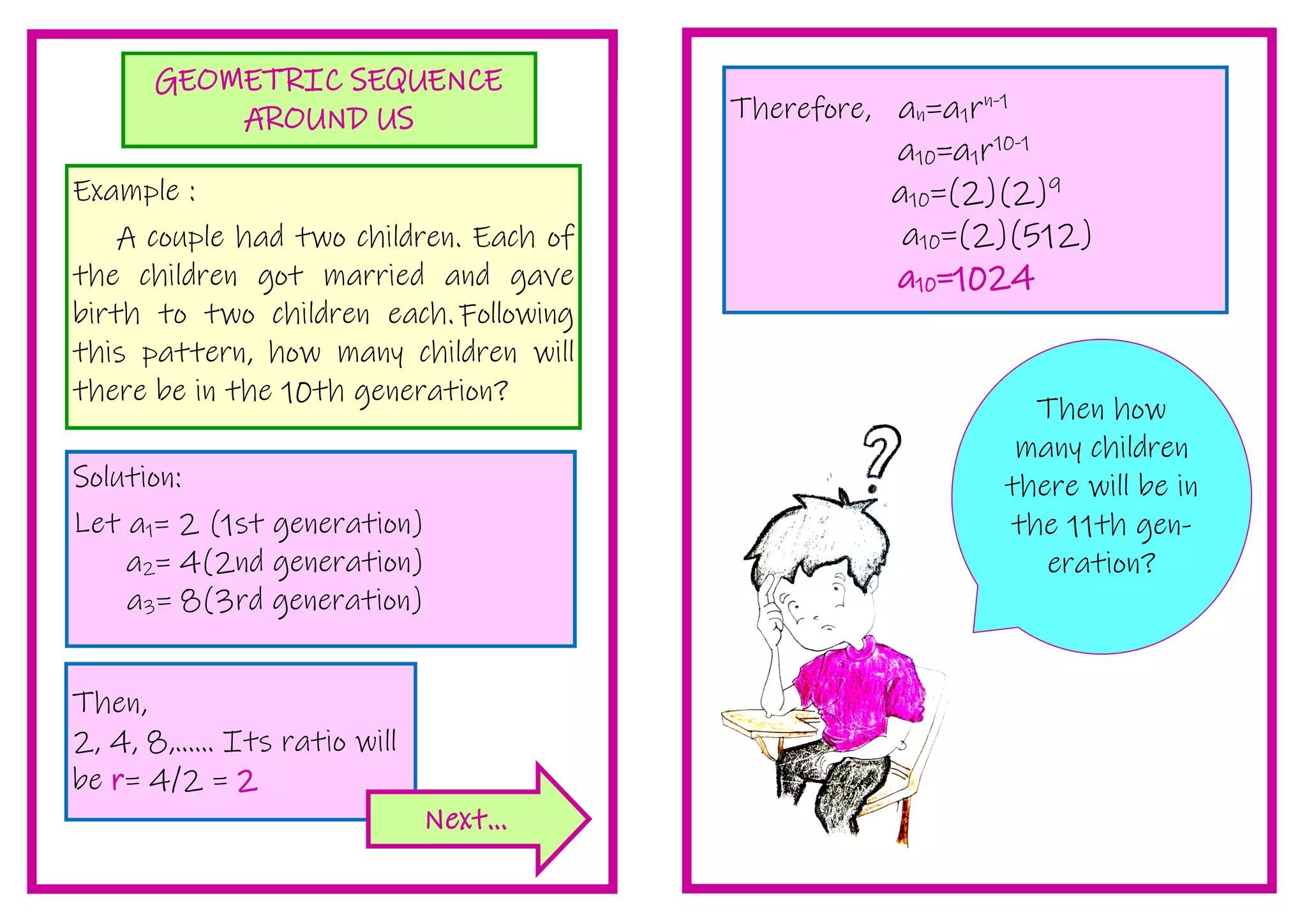
1. This document provides instruction on determining the nth term and geometric means of geometric sequences. It includes examples of finding the nth term, common ratio, and inserting terms. 2. Students are provided activities to practice finding the nth term and geometric means of sequences. This includes word problems applying geometric sequences. 3. Additional enrichment material is given to further reinforce the concepts through extended examples and a word problem calculating savings over time with interest.

1. determines geometric means and nth term of a geometric sequence
Department of Education
Region III
Schools Division of Zambales
BAQUILAN RESETTLEMENT HIGH SCHOOL
Botolan
HILDA D. DRAGON
Teacher II
Baquilan Resett lement High School
The only way
to learn
Mathematics
is to
do Mathematics.
-Paul Halmos

2. OBJECTIVES:
1. Determines geometric means
and nth term of a geometric se-
quence.
2. Solve real-life problems involving
geometric sequence.
LEAST MASTERED SKILLS
The learner determines geo-
metric means and nth term of a
geometric sequence.
LC CODE: M10AL-Ie-1

8. Find the nth term in the follow-
ing geometric sequences.
1. 5th term if the 1st term is 5 and
the common ratio is 4
2. 6th term of the sequence 1, 4, 16,
64, . . .
3. 4th term of the sequence if the 1st
term is 5 and the common ratio is 2
4. 7th term of the sequence 3, 15, 75,
5. 10th term of the sequence 1/3, 1, ..
Find the indicated number of
geometric means between each pair
of numbers.
1. 120 and 30 (1)
2. 5 and 40 (2)
3. 6 and 1296 (2)
4. -2 and –32 (3)
5. 1/4 and 64 (3)
Solve.
Sharon is raising chickens as a source of
additional income. Among the chickens that she
was raising, she chose to observe several of
them as possible egg layers. She gathered 3
eggs on the first day, 6 on the second and 12
on the third day. How many eggs will she ex-
pect to gather on the 10th day?

9. Find the ratio of the second number to the
first number:
5 and 15
Then 15:5 is also 15/5. That is eaqual to 3/1
0r 3.
Try another: -28 and –7
It will be –7:-28 or –7/-28. That is eqaul to
1/4.
Let’s review ratio. What is a ratio?
A ratio is a relationship between two
numbers. It is very important in solv-
ing problems in geometric sequence.
How to find a ratio? Write the ratio
as a fraction. Ex. the ratio of 9 to 27.
Since both numbers are divisible by 9,
reduced it to lowest form. The ratio
Before you begin this lesson, remember
this:
Mistakes are proof
that you are trying..
So, try and try....always be positive.
I know you can do it!
Enjoy your journey,
goodluck!!

10. The Rule of a Geometric Sequence
It goes like this:
1, 2, 4, 8
Questions:
1. What did you observe
in the illustration above?
2. What do you think is
the 5th number?
A geometric sequence is a se-
quence where each term after the
first is obtained by multiplying the
preceding term by a nonzero con-
stant called the common ratio.
A common ratio, r, can be deter-
mined by dividing any term in the se-
quence by the term that precedes
it.
Thus in the geometric
sequence 27, 9, 3, 1,
...the common ratio is
1/3 since 9/27=1/3.

11. Example 2: Find the 10th
term of the
geometric sequence:
729, 243, 81, 27,...
Solution:
Since 243/729 is 1/3 3, then:
an=a1rn-1
a10=a1r10-1
a10=(729)(1/3)9
a10=(729)(1/3)9
a10=(729)(1/19683)
a10=1/27
Given the 1st term a1 and the com-
mon ratio r of a geometric sequence, the
nth
term of a geometric sequence is:
Next...
Example 1:
What is the 8th
term of the geomet-
ric sequence 1, 3, 9, 27, ...?
Solution:
Since 3/1 is 3, then:
an=a1rn-1
a8=a1r8-1
a8=(1)(3)7
a8=(1)(3)7

12. Solution:
Let a1=16 and a4=1024. We will in-
sert a2 and a3.
Since a4=a1rn-1
1024= 16 r3
1024= 16 r3
16 16
64= r3
4= r
Then,
a2=16 (4)1
a2=64
and
a3=16 (4)2
a3=16(16)
a3=256
This is how to do it...
Inserting number of terms
between two given terms of geo-
metric sequence. We call the
terms between any two given
terms of a geometric sequence
the geometric means.
There’s more on
Geometric Sequence...
Example 1:
Insert two geometric means be-
tween 16 and 1024.

13. Solution:
Let a1= 2 (1st generation)
a2= 4(2nd generation)
a3= 8(3rd generation)
Then,
2, 4, 8,...... Its ratio will
be r= 4/2 = 2
Therefore, an=a1rn-1
a10=a1r10-1
a10=(2)(2)9
a10=(2)(512)
a10=1024
GEOMETRIC SEQUENCE
AROUND US
Example :
A couple had two children. Each of
the children got married and gave
birth to two children each. Following
this pattern, how many children will
there be in the 10th generation?
Next...
Then how
many children
there will be in
the 11th gen-
eration?

14. Activity 1. Missing You
Find the nth term in the
following geometric se-
quences.
1. 4th
term if the 1st
term is 4 and the
common ratio is 4
2. 5th
term of the se-
quence 6, 36,...
3. 6th
term of the
sequence if the 1st
term is 7 and the
common ratio is 2
4. 7th
term of the
sequence 3,12, 48, .
5. 8th term of the
sequence 1/2, 1, ..
Activity 2. What Do You Mean?
Find the indicated number of geometric
means between each pair of numbers.
1. 10 and 80 (2)
2. 7 and -7 (2)
3, 243 and 3 (3)
4. 8 and 648 (3)
5. 1/4 and 64 (3)
Activity 3. Fold it up
Suppose you are holding
a piece of paper which is
0.02 inch thick. Each time
you fold the paper in half,
its thickness is doubled.
What will be its thickness
if you fold it ten times?

15. A.What’s Missing?
Find the nth term in the following geo-
metric sequences.
1. 5th
term if the 1st
term is 5 and the
common ratio is 5
2. 6th
term of the sequence 7, 49,...
3. 7th
term of the sequence if the 1st
term is 8 and the common ratio is 3
4. 5th
term of the sequence 8,16, 32, . .
5. 4th
term of the sequence 1/3, 1, ..
B. You Mean To Me
Find the indicated number
of geometric means be-
tween each pair of num-
bers.
1. 12 and 192 (3)
2. 8 and 648 (3)
3, 1280 and 5 (3)
4. 1312 and 41 (4)
5. 1 and 7168 (4)
C. Through the Years
Manny gave Minda 3 red roses on
their 1st wedding anniversary, 12 on their
2nd, 48 on their 3rd and so on. How many
roses will Minda receive on their 6th wed-
ding anniversary?

16. Enrichment. Save Me
Ana deposited
P10,000 in a bank.
He planned to save
that amount for his
son’s future. The
bank gives a 7% in-
terest per annum.
How much will his
savings be at the
end of 5 years?
Enrichment Card
Mang Pepe’s savings at
the end of five years will
therefore be P14,025.52

17. Pre-test
A.
1. 1280
2. 1024
3. 40
4. 46, 875
5. 6561
B.
1. 60
2. 10, 20
3. 36, 216
4. -4, -8, -16
5. 1, 4, 16
C.
a10=1536
Activity Card
Activity 1
1. 1024
2. 7776
3. 224
4. 12288
5. 64
Activity 2
1. 20, 40
2. 7, -7
3. 81, 27, 9
4. 24, 72, 216
5. 1, 4, 16
Activity 3
a10=10.24

18. Assessment Card
Activity 1
1. 3125
2. 2401
3. 46656
4. 32768
5. 9
Activity 2
1. 24, 48, 96
2. 24, 72, 216
3. 320, 80, 20
4. 656, 328, 164, 82
5. 28, 112, 448, 1792
Activity 3
a6=3072
Department of Education 2015. Mathe-
matics 10 Learning Module. Pasig City,
Philippines:REX Book Store, Inc.
https://www.onlinemathlearning.com/
geometric-sequences.html
https://lrmds.deped.gov.ph/search?
fil-
ter=&search_param=all&query=GEOME
TRIC+SEQUENCE
https://www.shmoop.com/sequences-
series/geometric-sequences-
exercises.html