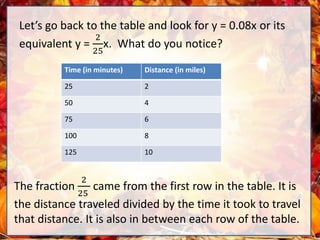
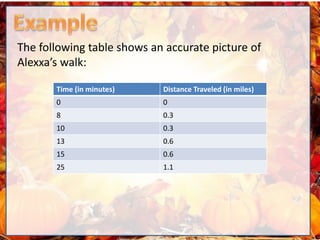
- The document discusses proportional relationships between distance and time when speed is constant. It provides examples of using ratios, proportions, and linear equations to solve problems about distance and time given average or constant speed. - Key concepts covered include defining average speed, identifying when constant speed can be assumed to use proportions, and writing linear equations relating distance and time under conditions of constant speed. - Students are encouraged to practice basic ratio and proportion skills in preparation for working on proportional relationship word problems over two class periods.

1. Learning Targets ….
• Students work with proportional relationships that
involve average speed and constant speed in order to
write a linear equation in two variables.
• Students use linear equations in two variables to
answer questions about distance and time.

2. Yesterday, we introduced Unit 3.
Next week - No Live Classes!

3. Agenda
 Review
 Ratio vs. Rate
 Unit Rate
 Proportions
 Proportional Relationships

4. Paul walks 2 miles in 25 minutes. How many miles can
Paul walk in 137.5 minutes?
How many miles would he walk in 50 minutes?
How many miles would he walk in 75 minutes?
How many miles would he walk in 100 minutes?
How many miles would he walk in 125 minutes?

5. Paul walks 2 miles in 25 minutes. How many miles can
Paul walk in 137.5 minutes?
Time (in minutes) Distance (in miles)

6. A ratio is a comparison between two similar
things.
Ratio: 4
3
Rate: 90 miles
3 hours
Read as
“90 miles per 3 hours.”
A rate is a comparison of two quantities
that have different units.

7. Since the relationship between the distance Paul walks
and the time it takes him to walk that distance is
proportional, we let y represent the distance Paul walks in
137.5 minutes and write the following:
25
2
=
137.5
𝑦

9. Tell whether the ratios are proportional.
4
10
6
15
Since the cross products are equal, the ratios are
proportional.
60
=
?
Example: Using Cross Products to Identify
Proportions
60 = 60
Find cross products.
60
4
10
6
15

10. Example: Using Cross Products to Identify
Proportions
A mixture of fuel for a certain small engine
should be 4 parts gasoline to 1 part oil. If
you combine 5 quarts of oil with 15 quarts
of gasoline, will the mixture be correct?
4 parts gasoline
1 part oil
=
? 15 quarts gasoline
5 quarts oil
4 • 5 = 20 1 • 15 = 15
20 ≠ 15
The cross products are not equal. The mixture will
not be correct.
Set up equal
ratios.
Find the cross
products.

11. The ratio of boys to girls in a soccer league is
5:4. If there are 52 boys in the league, how
many girls are there?
Write a ratio comparing girls to
boys.
Set Up the proportion. Let x
represent the number of girls.
5
4
girls
boys
=
Since x is divided by 52, multiply
both sides of the equation by 56.
5
4
= x
52
65 = x
(52) (52)5
4
= x
52
There are 65 girls in the league.

12. A cable car travels 15 miles in 80 minutes. At
this rate of speed, how long would it take the
cable car to travel 45 miles?
15 ▪ s = 80 ▪ 45
Set up a proportion that
compares distance to time.
Let s represent the time
the takes to travel 45 mi.
distance 1
time 1
=
distance 2
time 2
At a constant rate of speed ratios of distance to
time are equivalent.
Find the cross products.
15 mi
80 min
= 45 mi
s

13. How many miles, y, can Paul walk in x minutes?
We know for a fact that Paul can walk 2 miles in 25
minutes, so we can write the ratio
25
2
as we did with the
proportion. We can write another ratio for the number
of miles, y, Paul walks in x minutes. It is
𝑥
𝑦
. For the same
reason we could write the proportion before, we can
write one now with these two ratios:

14. How many miles, y, can Paul walk in x minutes?
25
2
=
𝑥
𝑦
Does this remind you of something we have recently
done?
It’s a linear equation in disguise!!!!!

15. 25
2
=
𝑥
𝑦
Paul can walk y miles in 0.08x minutes. This equation will
allow us to answer all kinds of questions about Paul with
respect to any given number of minutes or miles.

16. Time (in minutes) Distance (in miles)
25 2
50 4
75 6
100 8
125 10
Let’s go back to the table and look for y = 0.08x or its
equivalent y =
2
25
x. What do you notice?
The fraction
2
25
came from the first row in the table. It is
the distance traveled divided by the time it took to travel
that distance. It is also in between each row of the table.

17. Unit rates are rates in which the second
quantity is 1.
unit rate: 30 miles,
1 hour
or 30 mi/h
The ratio 90
3
can be simplified by dividing:
90
3
= 30
1

18. Penelope can type 90 words in 2 minutes. How
many words can she type in 1 minute?
90 words
2 minutes
Write a rate.
=
Penelope can type 45 words in one minute.
90 words ÷ 2
2 minutes ÷ 2
Divide to find words
per minute.
45 words
1 minute

19. Geoff can type 30 words in half a minute. How
many words can he type in 1 minute?
Write a rate.
=
Geoff can type 60 words in one minute.
Multiply to find
words per
minute.
60 words
1 minute
30 words
minute
1
2
30 words • 2
minute • 2
1
2

20. Time (in hours) Distance (in miles)
3 123
6 246
9 369
12 492
y
We want to know how many miles, y, can be
traveled in any number of hours x.

21. What does the equation y = 41x mean?

22. Consider the following word problem: Alexxa walked
from Grand Central Station on 42nd Street to Penn
Station on 7th Avenue. The total distance traveled was
1.1 miles. It took Alexxa 25 minutes to make the walk.
How many miles did she walk in the first 10 minutes?

23. Are you sure about your answer? How often do you
walk at a constant speed? Notice the problem did not
even mention that she was walking at the same rate
throughout the entire 1.1 miles.
What if you have more information about her walk:
Alexxa walked from Grand Central Station (GCS) along
42nd Street to an ATM machine 0.3 miles away in 8
minutes. It took her 2 minutes to get some money out
of the machine. Do you think your answer is still
correct?

24. Let’s continue with Alexxa’s walk: She reached the 7th
Avenue junction 13 minutes after she left GCS, a
distance of 0.6 miles. There, she met her friend Karen
with whom she talked for 2 minutes. After leaving her
friend, she finally got to Penn Station 25 minutes after
her walk began.
Is this a more realistic situation than believing that she
walked the exact same speed throughout the entire
trip? What other events typically occur during walks in
the city?

25. Time (in minutes) Distance Traveled (in miles)
0 0
8 0.3
10 0.3
13 0.6
15 0.6
25 1.1
The following table shows an accurate picture of
Alexxa’s walk:

26. Now that we have an idea of what could go wrong
when we assume a person walks at a constant rate or
that a proportion can give us the correct answer all of
the time, let’s define what is called average speed.
Suppose a person walks a distance of d (miles) in a
given time interval t (minutes). Then, the average
speed in the given time interval is
𝑑
𝑡
in miles per
minute.

27. Suppose a person walks a distance of d (miles) in a
given time interval t (minutes). Then, the average
speed in the given time interval is
𝑑
𝑡
in miles per
minute.
With this definition we can calculate Alexxa’s average
speed: The distance that Alexxa traveled divided by the
time interval she walked is
1.1
25
miles per minute.

28. If we assume that someone can actually walk at the
same average speed over any time interval, then we say
that the person is walking at a constant speed. Suppose
the average speed of a person is the same constant C
for any given time interval. Then, we say that the
person is walking at a constant speed C.

29. If the original problem included information specifying
constant speed, then we could write the following:
Alexxa’s average speed for 25 minutes is
1.1
25
. Let y
represent the distance Alexxa walked in 10 minutes.
Then, her average speed for 10 minutes is
𝑦
10
. Since
Alexxa is walking at a constant speed of C miles per
minute, then we know that
1.1
25
= C, and
𝑦
10
= C.

30. Since both fractions are equal to C, then we can write
1.1
25
=
𝑦
10
.
With the assumption of constant speed, we now have a
proportional relationship, which would make the
answer you came up with in the beginning correct.

31. We can go one step further and write a statement in
general. If Alexxa walks y miles in x minutes, then
𝑦
𝑥
= 𝐶 and
1.1
25
=
𝑦
𝑥
.
To find how many miles 𝑦𝑦 Alexxa walks in x miles, we
solve the equation for y:

32. • Average speed is found by taking the total distance
traveled in a given time interval, divided by the time
interval.
• If we assume the same average speed over any time
interval, then we have constant speed, which can
then be used to express a linear equation in two
variables relating distance and time.
• We know how to use linear equations to answer
questions about distance and time.
• We cannot assume that a problem can be solved
using a proportion unless we know that the
situation involves constant speed (or rate).

33. Questions???
We will work on this lesson for two days
Day 1:
Need to practice some basic ratio and proportion skills???
** IXL Skills: H.1 – H.9
Day 2:
Complete the Proportional Relationships Practice
Problems