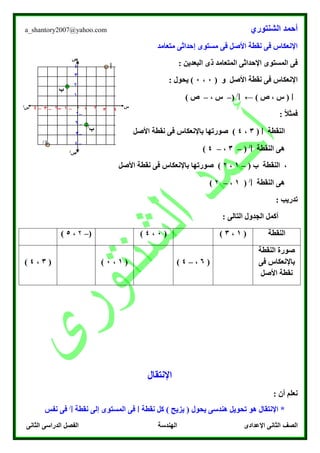
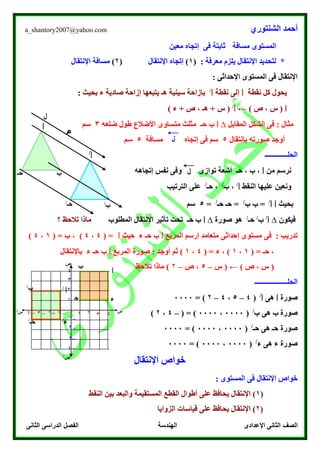
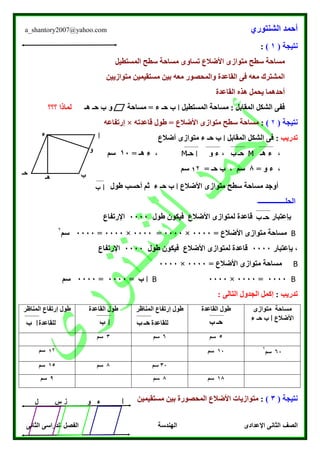
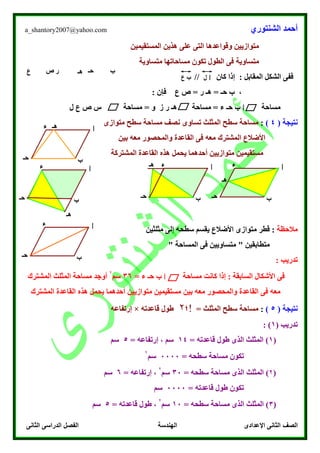
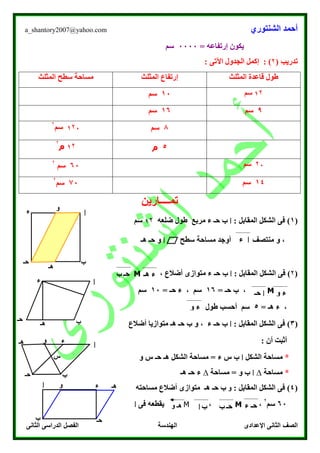
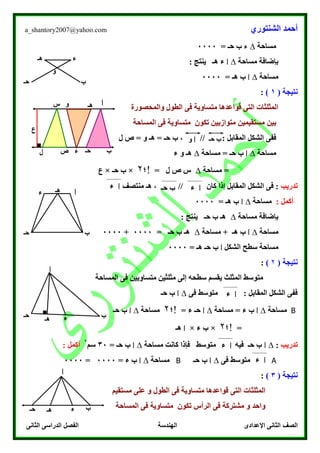
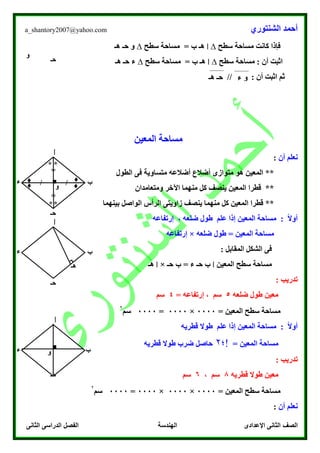
يتناول النص موضوع التحويلات الهندسية، مع التركيز على مفهوم الإنعكاس في المستوى الإحداثي. يقدم النص أمثلة توضيحية حول كيفية إيجاد صور الأشكال عقب إجراء عملية الإنعكاس على المحاور المختلفة. كما يتضمن تمارين تدريبية لتعزيز فهم الطلاب للمفاهيم والمبادئ المتعلقة بالانعكاس الهندسي.

1. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫الهندسية‬ ‫التحويالت‬
‫اإلنعكاس‬
: ‫أن‬ ‫نعلم‬
**‫له‬ ‫مطابق‬ ‫آخر‬ ‫هندسى‬ ‫شكل‬ ‫إلى‬ ‫الهندسى‬ ‫الشكل‬ ‫تحول‬ ‫هندسية‬ ‫تحويلة‬ ‫هو‬ ‫اإلنعكاس‬
‫نقطة‬ ‫كل‬ ‫يحول‬ ‫ل‬ ‫المستقيم‬ ‫فى‬ ‫اإلنعكاس‬ **‫ا‬‫إلى‬‫ا‬/
‫ب‬ ‫إلى‬ ‫ب‬ ،/
: ‫بحيث‬
‫كانت‬ ‫إذا‬‫ا‬h‫هو‬ ‫ل‬ ‫فإن‬ ‫ل‬‫الع‬‫ينصف‬ ‫الذى‬ ‫مود‬
‫ب‬ ‫كانت‬ ‫إذا‬g‫ب‬ ‫فإن‬ ‫ل‬≡‫ب‬/
‫ب‬ ‫كانت‬ ‫إذا‬ ‫أى‬g‫نفسها‬ ‫هى‬ ‫ب‬ ‫صورة‬ ‫فإن‬ ‫ل‬
: ‫اإلحداثى‬ ‫المستوى‬ ‫فى‬ ‫اإلنعكاس‬ **
(1‫كانت‬ ‫إذا‬ )‫ا‬‫صورتها‬ ‫فإن‬ ) ‫ص‬ ، ‫س‬ ( =‫باإلنعكاس‬: ‫هى‬ ‫السينات‬ ‫محور‬ ‫فى‬
‫ا‬/
، ‫س‬ ( =–) ‫ص‬
(۲‫كانت‬ ‫إذا‬ )‫ا‬: ‫هى‬ ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورتها‬ ‫فإن‬ ) ‫ص‬ ، ‫س‬ ( =
‫ا‬/
( =–) ‫ص‬ ، ‫س‬
‫مثال‬:‫المستطيل‬ ‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫مستوى‬ ‫فى‬‫ا‬‫حيث‬ ‫ء‬ ‫حـ‬ ‫ب‬
‫ا‬( =4،3( = ‫ب‬ ، )4،1)( = ‫حـ‬ ،1،3( = ‫ء‬ ، )1،1: ‫أوجد‬ ‫ثم‬ )
(1)‫صور‬‫ة‬‫المستطيل‬‫ا‬‫حـ‬ ‫ب‬‫ء‬‫محور‬ ‫فى‬ ‫باإلنعكاس‬‫السينات‬
(۲‫صورة‬ )‫المستطيل‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬
(3‫ضلع‬ ‫طول‬ ‫قس‬ )‫المستطيل‬ ‫أضالع‬ ‫من‬‫باإل‬ ‫وصورته‬ " ‫زاوية‬ ‫كل‬ ‫قياس‬ "‫وقارن‬ ‫نعكاس‬
‫؟‬ ‫تالحظ‬ ‫ماذا‬ ‫وأذكر‬ ‫بينهما‬
(4‫هل‬ ، // ، // ‫هل‬ )//،//
‫؟‬ ‫تالحظ‬ ‫ماذا‬ ‫وأذكر‬
‫الحلــــــــــــــــ‬
‫ا‬‫ا‬/
‫ل‬
‫ا‬‫ا‬/ ■
‫ب‬≡‫ب‬/
////
‫ا‬/
‫ب‬/
‫ء‬/
‫حـ‬/
‫ب‬/
‫حـ‬/
‫ا‬/
‫ء‬/
‫ا‬//
‫ب‬//‫ء‬//
‫حـ‬//
‫ب‬//
‫حـ‬//‫ا‬//
‫ء‬//

2. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(1‫مح‬ ‫فى‬ ‫باإلنعكاس‬ ): ‫السينات‬ ‫ور‬
‫صورة‬‫ا‬( =4،3‫هى‬ )‫ا‬/
( =4،–3)
‫ب‬ ‫صورة‬( =4،1‫ب‬ ‫هى‬ )/
( =4،–1)
‫حـ‬ ‫صورة‬( =1،3‫حـ‬ ‫هى‬ )/
( =1،–3)
‫ء‬ ‫صورة‬( =1،1‫ء‬ ‫هى‬ )/
( =1،–1)
B‫ا‬ ‫صورة‬‫لمستطيل‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
‫المستطيل‬ ‫هى‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬‫ا‬/
‫ب‬/
‫حـ‬/
‫ء‬/
(۲: ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ )
‫صورة‬‫ا‬( =4،3‫هى‬ )‫ا‬//
( =–4،3)
‫ب‬ ‫صورة‬( =4،1‫ب‬ ‫هى‬ )//
( =–4،1)
‫حـ‬ ‫صورة‬( =1،3‫حـ‬ ‫هى‬ )//
( =–1،3)
‫ء‬ ‫صورة‬( =1،1‫ء‬ ‫هى‬ )//
( =–1،1)
B‫المستطيل‬ ‫صورة‬‫ا‬‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫ء‬ ‫حـ‬ ‫ب‬‫الصاد‬‫المستطيل‬ ‫هى‬ ‫ات‬‫ا‬//
‫ب‬//
‫حـ‬//
‫ء‬//
(3: ‫أن‬ ‫نجد‬ ‫بالقياس‬ )‫ا‬= ‫ب‬‫ا‬/
‫ب‬/
=‫ا‬//
‫ب‬//
،‫ب‬ = ‫حـ‬ ‫ب‬/
‫حـ‬/
‫ب‬ =//
‫حـ‬//
،‫ا‬‫ء‬=‫ا‬/
‫ء‬/
=‫ا‬//
‫ء‬//
‫حـ‬ = ‫ء‬ ‫حـ‬ ،/
‫ء‬/
‫حـ‬ =//
‫ء‬//
،‫ق‬(‫ال‬‫ا‬= )‫ق‬(‫ال‬‫ا‬/
)،‫ق‬(‫ال‬= ) ‫ب‬‫ق‬(‫ال‬‫ب‬/
)
،‫ق‬(‫ال‬‫حـ‬= )‫ق‬(‫ال‬‫حـ‬/
)،‫ق‬(‫ال‬= ) ‫ء‬‫ق‬(‫ال‬‫ء‬/
)
‫أن‬ ‫نالحظ‬( :1‫المستقيمة‬ ‫القطع‬ ‫أطوال‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
(۲‫الزوايا‬ ‫قياسات‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
(3‫اإلنعكاس‬ )‫التوازى‬ ‫على‬ ‫يحافظ‬
‫هـ‬ ‫كانت‬ ‫إذا‬ : ‫تدريب‬g‫هـ‬ ‫عين‬/
‫؟‬ ‫تالحظ‬ ‫ماذا‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫هـ‬ ‫صورة‬
(4‫البينية‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
‫الشكل‬ ‫لرؤوس‬ ‫الدورانى‬ ‫الترتيب‬ ‫على‬ ‫يحافظ‬ ‫ال‬ ‫اإلنعكاس‬ : ‫أن‬ ‫الحظ‬
‫اإلنعكاس‬ ‫خواص‬
‫س‬‫س‬/
‫ص‬
‫ص‬/
–3
–۲
–1
۲
3
4
1
–4
1–3 –۲ –1 0 3 4۲–4
‫ا‬
‫ب‬
‫ح‬
‫ـ‬
‫ا‬//
‫ب‬/
‫ب‬//
‫حـ‬//
‫ء‬‫ء‬//
‫ء‬/
‫حـ‬/ ‫ا‬/
‫ا‬‫ب‬

3. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫فى‬ ‫اإلنعكاس‬ ‫خواص‬‫المستوى‬:
(1‫المستقيمة‬ ‫القطع‬ ‫أطوال‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
(۲‫الزوايا‬ ‫قياسات‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
(3‫التوازى‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
(4‫البينية‬ ‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ )
‫مالحظة‬:
‫يح‬ ‫الذى‬ ‫اإلنعكاس‬‫ل‬ ‫مستقيم‬ ‫فى‬ ‫باإلنعكاس‬ ‫نفسه‬ ‫إلى‬ ‫الشكل‬ ‫ول‬
‫تماثل‬ ‫محور‬ ‫الحالة‬ ‫هذه‬ ‫فى‬ ‫ل‬ ‫المستقيم‬ ‫ويسمى‬ ، ‫تماثل‬ ‫يسمى‬
‫تدريب‬(1):: ‫من‬ ‫كل‬ ‫تماثل‬ ‫محاور‬ ‫عدد‬ ‫أذكر‬
‫الساقين‬ ‫المتساوى‬ ‫المثلث‬ ، ‫األضالع‬ ‫المتساوى‬ ‫المثلث‬‫األضالع‬ ‫المختلف‬ ‫المثلث‬ ،
،‫األضالع‬ ‫متوازى‬ ، ‫المعين‬ ، ‫المستطيل‬ ، ‫المربع‬‫الساقين‬ ‫المتساوى‬ ‫المنحرف‬ ‫شبه‬ ،
( ‫تدريب‬۲: )
‫المثلث‬ ‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫مستوى‬ ‫فى‬‫ا‬‫حيث‬ ‫حـ‬ ‫ب‬‫ا‬( =4،3( = ‫ب‬ ، )3،1)
( = ‫حـ‬ ،1،4: ‫أوجد‬ ‫ثم‬ )
(1‫المثلث‬ ‫صورة‬ )‫ا‬‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫ب‬
(۲‫المثلث‬ ‫صورة‬ )‫ا‬‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫ب‬
‫الحلــــــــــــــــ‬
(1: ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ )
‫صورة‬‫ا‬( =4،3‫هى‬ )0000
‫ب‬ ‫صورة‬( =4،1‫هى‬ )0000
‫حـ‬ ‫صورة‬( =1،3‫هى‬ )0000
B‫المثلث‬ ‫صورة‬‫ا‬‫هى‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫ب‬0000
(۲: ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ )‫صورة‬‫ا‬( =4،3‫هى‬ )0000
‫ل‬
‫ا‬
‫ب‬////‫ح‬
‫ـ‬
■
‫س‬‫س‬/
‫ص‬
‫ص‬/
–3
–۲
–1
۲
3
4
1
–4
1–3 –۲ –1 0 3 4۲–4
‫ء‬

4. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫ب‬ ‫صورة‬( =4،1‫هى‬ )0000‫حـ‬ ‫صورة‬( =1،3)0000
B‫المثلث‬ ‫صورة‬‫ا‬‫هى‬ ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫ب‬0000
( ‫تدريب‬3):: ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫ا‬‫أضالعه‬ ‫منتصفات‬ ‫ل‬ ، ‫ع‬ ، ‫ص‬ ، ‫س‬ ، ‫مربع‬ ‫ء‬ ‫حـ‬ ‫ب‬
‫الترتيب‬ ‫على‬ ، ، ،،‫م‬‫قطريه‬ ‫منتصف‬‫أكمل‬:
(1‫صورة‬ )∆‫ا‬‫م‬‫هى‬ ‫فى‬ ‫باإلنعكاس‬ ‫س‬0000
،‫س‬‫م‬=0000‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ ‫ألن‬0000
،‫ق‬(‫ال‬‫ا‬‫م‬= )‫س‬0000‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ ‫ألن‬0000
(۲)‫ص‬ ‫حـ‬ ‫المربع‬‫م‬‫المربع‬ ‫صورة‬ ‫هو‬ ‫ع‬0000‫فى‬ ‫باإلنعكاس‬
(3‫المستطيل‬ ‫صورة‬ ‫ص‬ ‫ل‬ ‫ء‬ ‫حـ‬ ‫المستطيل‬ )‫ب‬‫ا‬‫فى‬ ‫باإلنعكاس‬ ‫ص‬ ‫ل‬0000
‫النقطة‬ ‫صورة‬ ‫ع‬ ‫النقطة‬ ،0000‫على‬ ‫يحافظ‬ ‫اإلنعكاس‬ ‫ألن‬0000
( ‫تدريب‬4):: ‫التالى‬ ‫الجدول‬ ‫أكمل‬
‫النقطـــــة‬
‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫النقطة‬ ‫صورة‬
‫ا‬‫لسينات‬‫الصادات‬
(1،3)(1،–3)(–1،3)
(–۲،5)
(0،4)
(1،0)
(–3،3)
(6،–4)
(3،4)
‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬
‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬‫م‬‫كل‬ ‫يحول‬‫نقطة‬‫ا‬‫المستوى‬ ‫فى‬‫نقطة‬ ‫إلى‬‫ا‬/
‫ا‬‫ب‬
‫حـ‬ ‫ب‬‫ء‬ ‫حـ‬‫ء‬‫ا‬‫ل‬
‫ا‬ ‫ب‬
‫ح‬
‫ـ‬
‫ء‬
‫س‬
‫ص‬
‫ع‬
‫م‬
=
=
=
=
‫اا‬‫اا‬
‫اا‬‫اا‬
‫ا‬‫ا‬/
‫م‬
‫ا‬
//
//

5. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫تكون‬ ‫بحيث‬ ‫المستوى‬ ‫نفس‬ ‫فى‬‫م‬‫منتصف‬
‫النقطة‬ ‫وتسمى‬‫م‬‫صورة‬ ‫وتكون‬ ، ‫اإلنعكاس‬ ‫مركز‬‫م‬‫فى‬ ‫باإلنعكاس‬‫م‬‫نفسها‬ ‫هى‬
‫قياسى‬ ‫تساوى‬ ‫هو‬ ‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬ : ‫فإن‬ ‫لذا‬
‫مثال‬:
‫أوجد‬ ‫المقابل‬ ‫الشكل‬ ‫فى‬‫صورة‬‫نقطة‬ ‫فى‬ ‫باإلنعكاس‬‫م‬
‫الحلــــــــــ‬
(1‫عليه‬ ‫ونعين‬ ‫نرسم‬ )‫ا‬/
‫بحيث‬‫ا‬/
‫م‬=‫ا‬‫م‬
(۲‫عليه‬ ‫ونعين‬ ‫نرسم‬ )‫ب‬/
‫ب‬ ‫بحيث‬/
‫م‬‫ب‬ =‫م‬
(3‫نقطة‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورة‬ ‫فتكون‬ ‫نرسم‬ )‫م‬
‫حـ‬ ‫كانت‬ ‫إذا‬ **g‫نقطة‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫صورة‬ ‫أوجد‬‫م‬‫؟‬ ‫تالحظ‬ ‫ماذا‬
**‫الشكل‬ ‫إسم‬ ‫أذكر‬‫ا‬‫ب‬‫ا‬/
‫ب‬/
‫اإلنعكاس‬ ‫خواص‬: ‫نقطة‬ ‫فى‬
(1)‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬‫النقط‬ ‫بين‬ ‫والبعد‬ ‫المستقيمة‬ ‫القطع‬ ‫أطوال‬ ‫على‬ ‫يحافظ‬
(۲)‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬‫الزوايا‬ ‫قياسات‬ ‫على‬ ‫يحافظ‬
(3‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬ )‫التوازى‬ ‫على‬ ‫يحافظ‬
(4)‫يحافظ‬ ‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬‫اإلتجا‬ ‫على‬‫الشكل‬ ‫رؤوس‬ ‫لترتيب‬ ‫الدورانى‬ ‫ه‬
‫تعريف‬‫متوازيين‬ ‫متقابلين‬ ‫ضلعين‬ ‫كل‬ ‫فيه‬ ‫رباعى‬ ‫شكل‬ ‫هو‬ ‫األضالع‬ ‫متوازى‬ :
‫األضالع‬ ‫متوازى‬ ‫خواص‬:(1‫متساويا‬ ‫متقابلين‬ ‫ضلعين‬ ‫كل‬ )‫الطول‬ ‫فى‬ ‫ن‬
(۲‫متساويتا‬ ‫متقابلتين‬ ‫زاويتين‬ ‫كل‬ )‫القياس‬ ‫فى‬ ‫ن‬
(3‫اآلخر‬ ‫منهما‬ ‫كل‬ ‫ينصف‬ ‫القطران‬ )
‫مالحظة‬‫األضالع‬ ‫متوازى‬ ‫من‬ ‫خاصة‬ ‫حاالت‬ ‫هى‬ ‫والمربع‬ ‫والمستطيل‬ ‫المعين‬ :
‫والمربع‬ ‫والمستطيل‬ ‫المعين‬ : ‫من‬ ‫كل‬ ‫خواص‬ ‫أذكر‬
‫ا‬/
‫م‬
‫ا‬
‫ا‬/
‫ب‬
‫ب‬/
‫ا‬‫ب‬
‫ا‬
‫م‬
‫ب‬
‫م‬
‫ا‬/
‫ب‬/
‫ا‬/
‫ب‬/
‫ا‬‫ب‬
‫ا‬‫ب‬

6. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫متعامد‬ ‫إحداثى‬ ‫مستوى‬ ‫فى‬ ‫األصل‬ ‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬
‫ذى‬ ‫المتعامد‬ ‫اإلحداثى‬ ‫المستوى‬ ‫فى‬: ‫البعدين‬
( ‫و‬ ‫األصل‬ ‫نقطة‬ ‫فى‬ ‫اإلنعكاس‬0،0: ‫يحول‬ )
‫ا‬) ‫ص‬ ، ‫س‬ (←‫ا‬/
(–، ‫س‬–) ‫ص‬
: ً‫ال‬‫فمث‬
‫النقطة‬‫ا‬(3،4‫األصل‬ ‫نقطة‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورتها‬ )
‫النقطة‬ ‫هى‬‫ا‬/
(–3،–4)
( ‫ب‬ ‫النقطة‬ ،–1،۲‫نقط‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورتها‬ )‫األصل‬ ‫ة‬
‫النقطة‬ ‫هى‬‫ا‬/
(1،–۲)
: ‫تدريب‬
: ‫التالى‬ ‫الجدول‬ ‫أكمل‬
‫النقطة‬(1،3)(0،4)(–۲،5)
‫النقطة‬ ‫صورة‬
‫فى‬ ‫باإلنعكاس‬
‫األصل‬ ‫نقطة‬
(6،–4)(1،0)(3،4)
‫اإلنتقال‬
: ‫أن‬ ‫نعلم‬
‫هندسى‬ ‫تحويل‬ ‫هو‬ ‫اإلنتقال‬ *‫ي‬‫حول‬‫نقطة‬ ‫كل‬ ) ‫يزيح‬ (‫ا‬‫المستوى‬ ‫فى‬‫نقطة‬ ‫إلى‬‫ا‬/
‫نفس‬ ‫فى‬
‫ا‬
‫ب‬
‫ب‬/
‫ا‬/
‫س‬‫س‬/
‫ص‬
‫ص‬/
–3
–۲
–1
۲
3
4
1
–4
1–3 –۲ –1 0 3 4۲–4

7. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫المستوى‬‫مسافة‬‫معين‬ ‫إتجاه‬ ‫فى‬ ‫ثابتة‬
‫معرفة‬ ‫يلزم‬ ‫اإلنتقال‬ ‫لتحديد‬ *( :1)‫اإلنتقال‬ ‫إتجاه‬(۲)‫اإلنتقال‬ ‫مسافة‬
: ‫اإلحداثى‬ ‫المستوى‬ ‫فى‬ ‫اإلنتقال‬
‫نقطة‬ ‫كل‬ ‫يحول‬‫ا‬‫نقطة‬ ‫إلى‬‫ا‬/
‫بحيث‬ ‫ء‬ ‫صادية‬ ‫إزاحة‬ ‫يتبعها‬ ‫هـ‬ ‫سينية‬ ‫بإزاحة‬:
‫ا‬) ‫ص‬ ، ‫س‬ (←‫ا‬/
) ‫ء‬ + ‫ص‬ ، ‫هـ‬ + ‫س‬ (
: ‫مثال‬‫المقابل‬ ‫الشكل‬ ‫فى‬∆‫ا‬‫حـ‬ ‫ب‬‫ضلعه‬ ‫طول‬ ‫األضالع‬ ‫متساوى‬ ‫مثلث‬3‫سم‬
‫بإنتقال‬ ‫صورته‬ ‫أوجد‬5‫إتجاه‬ ‫فى‬ ‫سم‬‫مسافة‬5‫سم‬
‫الحلـــــــــــــ‬
‫من‬ ‫نرسم‬‫ا‬‫إتجاهه‬ ‫نفس‬ ‫وفى‬ ‫توازى‬ ‫أشعة‬ ‫حـ‬ ، ‫ب‬ ،
‫النقط‬ ‫عليها‬ ‫ونعين‬‫ا‬/
‫ب‬ ،/
‫حـ‬ ،/
‫الترتيب‬ ‫على‬
‫بحيث‬‫ا‬‫ا‬/
‫ب‬ =‫ب‬/
‫حـ‬ =‫حـ‬/
=5‫سم‬
‫فيكون‬∆‫ا‬/
‫ب‬/
‫حـ‬/
‫صورة‬ ‫هو‬∆‫ا‬‫المطلوب‬ ‫اإلنتقال‬ ‫تأثير‬ ‫تحت‬ ‫حـ‬ ‫ب‬‫؟‬ ‫تالحظ‬ ‫ماذا‬
‫إحد‬ ‫مستوى‬ ‫فى‬ : ‫تدريب‬‫المربع‬ ‫إرسم‬ ‫متعامد‬ ‫اثى‬‫ا‬‫حيث‬ ‫ء‬ ‫حـ‬ ‫ب‬‫ا‬( =4،4( = ‫ب‬ ، )1،4)
( = ‫حـ‬ ،1،1( = ‫ء‬ ، )4،1‫المربع‬ ‫صورة‬ : ‫أوجد‬ ‫ثم‬ )‫ا‬‫باإلنتقال‬ ‫ء‬ ‫حـ‬ ‫ب‬
) ‫ص‬ ، ‫س‬ (←‫س‬ (–5‫ص‬ ،–۲‫تالحظ‬ ‫ماذا‬ )
‫ال‬‫حلـــــــــــــــــــ‬
‫صورة‬‫ا‬‫هى‬‫ا‬/
(4–5،4–۲= )0000
‫ب‬ ‫هى‬ ‫ب‬ ‫صورة‬/
(0000،0000( = )–4،۲)
‫حـ‬ ‫هى‬ ‫حـ‬ ‫صورة‬/
(0000،0000= )0000
‫صورة‬‫ء‬‫هى‬‫ء‬/
(0000،0000= )0000
‫اإلن‬ ‫خواص‬‫تقال‬
‫اإلنتقال‬ ‫خواص‬: ‫المستوى‬ ‫فى‬
(1‫اإلنتقال‬ )‫المس‬ ‫القطع‬ ‫أطوال‬ ‫على‬ ‫يحافظ‬‫تقيمة‬‫النقط‬ ‫بين‬ ‫والبعد‬
(۲‫اإلنتقال‬ )‫الزوايا‬ ‫قياسات‬ ‫على‬ ‫يحافظ‬
‫ل‬
‫م‬
‫ا‬
‫ا‬/
‫ب‬‫حـ‬
‫ب‬/‫حـ‬/
‫م‬
‫م‬
‫س‬‫س‬/
‫ص‬
‫ص‬/
–3
–۲
–1
۲
3
4
1
–4
1–3 –۲ –1 0 3 4۲–4
‫ا‬
‫ب‬
‫ح‬
‫ـ‬
‫ب‬/
‫ء‬
‫ء‬/
‫حـ‬/
‫ا‬/

8. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(3‫اإلنتقال‬ )‫التوازى‬ ‫على‬ ‫يحافظ‬
: ‫أن‬ ‫كما‬‫اإلنتقال‬‫الهندسى‬ ‫الشكل‬ ‫لرؤوس‬ ‫الدوارنى‬ ‫الترتيب‬ ‫على‬ ‫يحافظ‬
‫تدريب‬(1): ‫المقابل‬ ‫الشكل‬ ‫فى‬ :∆‫ا‬‫حـ‬ ‫ب‬‫األضالع‬ ‫متساوى‬‫ضلعه‬ ‫طول‬4‫سم‬
‫و‬ ، ‫هـ‬ ، ‫ء‬ ،: ‫يأتى‬ ‫ما‬ ‫أكمل‬ ‫الترتيب‬ ‫على‬ ، ، ‫منتصفات‬
(1)‫صورة‬∆‫هـ‬ ‫ء‬ ‫ب‬‫مسافة‬ ‫بإنتقال‬۲‫إتجاه‬ ‫فى‬ ‫سم‬
‫هى‬0000= ‫هـ‬ ‫ء‬ ،0000‫ألن‬‫على‬ ‫يحافظ‬ ‫اإلنتقال‬0000
(۲)∆‫صورة‬ ‫هـ‬ ‫ء‬ ‫ب‬∆‫مسافة‬ ‫بإنتقال‬ ‫حـ‬ ‫و‬ ‫هـ‬0000‫سم‬
‫إتجاه‬ ‫فى‬0000
(3)∆0000‫صورة‬∆‫ا‬‫مسافة‬ ‫بإنتقال‬ ‫ء‬ ‫و‬۲‫إتجاه‬ ‫فى‬ ‫سم‬
( ‫تدريب‬۲):: ‫التالى‬ ‫الجدول‬ ‫أكمل‬
‫النقطة‬(4،3)(۲،–3)(1،–5)
‫صورة‬
‫النقطة‬
‫باإلنتقال‬
) ‫ص‬ ، ‫س‬ (←+ ‫س‬ (1‫ص‬ ،–۲)
) ‫ص‬ ، ‫س‬ (←+ ‫س‬ (1‫ص‬ ،–۲)
) ‫ص‬ ، ‫س‬ (←(–1،5)
( ‫تدريب‬3):‫إرسم‬∆‫ا‬‫حـ‬ ‫ب‬‫فيه‬ ‫ب‬ ‫فى‬ ‫الزاوية‬ ‫قائم‬‫ا‬= ‫ب‬4= ‫حـ‬ ‫ب‬ ، ‫سم‬3: ‫أوجد‬ ‫ثم‬ ‫سم‬
‫مسافة‬ ‫بإنتقال‬ ‫صورته‬3‫إتجاه‬ ‫فى‬ ‫سم‬
‫صو‬ ،‫مسافة‬ ‫بإنتقال‬ ‫رته‬6‫إتجاه‬ ‫فى‬ ‫سم‬
‫الدوران‬
: ‫أن‬ ‫نعلم‬
‫هندسية‬ ‫تحويلة‬ ‫هو‬ ‫المستوى‬ ‫فى‬ ‫الدوران‬ *‫معينة‬ ‫بزاوية‬ ‫نقطة‬ ‫حول‬ ‫الشكل‬ ‫تدور‬
*‫النقطة‬ ‫حول‬ ‫الدوران‬‫م‬‫نقطة‬ ‫كل‬ ‫يحول‬ ‫هـ‬ ‫قياسها‬ ‫بزاوية‬‫ا‬‫المستوى‬ ‫فى‬
‫نقط‬ ‫إلى‬‫ة‬‫ا‬/
: ‫بحيث‬ ‫المستوى‬ ‫نفس‬ ‫فى‬
(1)‫ق‬(‫ال‬‫ا‬‫م‬‫ا‬/
)‫هـ‬ =(۲)‫م‬‫ا‬/
=‫م‬‫ا‬
‫ا‬‫ب‬‫حـ‬ ‫ب‬‫حـ‬‫ا‬
‫ا‬
‫ب‬‫ح‬
‫ـ‬
‫ء‬
‫ه‬
‫ـ‬
‫و‬
‫ا‬‫حـ‬
‫ا‬
‫ه‬
‫ـ‬
//

9. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫بالرمز‬ ‫له‬ ‫يرمز‬ ‫و‬( ‫د‬‫م‬: ‫حيث‬ ) ‫هـ‬ ،
(1)‫م‬‫الدوران‬ ‫مركز‬(۲)‫الدوران‬ ‫زاوية‬ ‫قياس‬ ‫هـ‬(3)‫الدوران‬ ‫إتجاه‬
‫مالحظات‬:
(1)‫الدوران‬ ‫إتجاه‬ ، ‫زاويته‬ ‫قياس‬ ، ‫الدوران‬ ‫مركز‬ ‫تحديد‬ ‫عند‬ ً‫ا‬‫تمام‬ ‫يتحدد‬ ‫الدوران‬
(۲)‫كان‬ ‫إذا‬ ً‫ا‬‫موجب‬ ‫يكون‬ ‫الدوران‬ ‫زاوية‬ ‫قياس‬‫الساعة‬ ‫عقارب‬ ‫إتجاه‬ ‫ضد‬ ‫الدوران‬
‫كان‬ ‫إذا‬ ً‫ا‬‫سالب‬ ‫ويكون‬ ،‫الساعة‬ ‫عقارب‬ ‫إتجاه‬ ‫مع‬ ‫الدوران‬
‫الدوران‬‫المستوى‬ ‫فى‬: ‫اإلحداثى‬
: ) ‫و‬ ( ‫األصل‬ ‫نقطة‬ ‫حول‬ ‫الدوران‬
(1)‫قياسها‬ ‫بزاوية‬00ْ( ‫النقطة‬ ‫إلى‬ ) ‫ص‬ ، ‫س‬ ( ‫النقطة‬ ‫يحول‬–) ‫س‬ ، ‫ص‬
(۲)‫قياسها‬ ‫بزاوية‬±180ْ( ‫النقطة‬ ‫إلى‬ ) ‫ص‬ ، ‫س‬ ( ‫النقطة‬ ‫يحول‬–، ‫س‬–) ‫ص‬
(3)‫قياسها‬ ‫بزاوية‬۲07‫أو‬ ْْ–00ْ‫ا‬ ‫يحول‬، ‫ص‬ ( ‫النقطة‬ ‫إلى‬ ) ‫ص‬ ، ‫س‬ ( ‫لنقطة‬–) ‫س‬
(4)‫قياسها‬ ‫بزاوية‬180ْ‫الصادات‬ ‫محور‬ ‫فى‬ ‫بإنعكاس‬ ً‫ا‬‫متبوع‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫إنعكاس‬ ‫يكاف‬
(5)‫قياسها‬ ‫بزاوية‬180‫أو‬ ْْ–180ْْ(‫دورة‬ ‫نصف‬ ‫دوران‬ ‫يسمى‬)" ‫متكافئان‬ ‫وهما‬ "
‫ا‬ ‫نقطة‬ ‫فى‬ ‫إنعكاس‬ ‫يكافئان‬ ‫و‬‫ألصل‬
(6)‫قياسها‬ ‫بزاوية‬360‫أو‬ ْْ–360ْ‫األصلى‬ ‫وضعه‬ ‫إلى‬ ‫الشكل‬ ‫يحول‬ ‫ألنه‬ ‫محايد‬ ‫دوران‬ ‫يسمى‬
‫نفسها‬ ‫النقطة‬ ‫على‬ ‫منطبقة‬ ‫نقطة‬ ‫كل‬ ‫صورة‬ ‫وتكون‬ ،
(7)‫قياسها‬ ‫بزاوية‬–۲07ْ‫قياسها‬ ‫بزاوية‬ ‫الدوران‬ ‫يكاف‬00ْْ
: ‫مثال‬
‫المقاب‬ ‫الشكل‬ ‫فى‬: ‫ل‬‫صورة‬ ‫أوجد‬‫حول‬ ‫بالدوران‬‫م‬‫قياسها‬ ‫بزاوية‬60ْْ
‫الحلـــــــــــــــــ‬
‫المنقلة‬ ‫بمركز‬ ‫ونركز‬ ‫الشعاع‬ ‫نرسم‬ **‫على‬‫م‬‫يشير‬ ‫بحيث‬
‫صفر‬ ‫الرقم‬ ‫إلى‬‫نرسم‬ ‫ثم‬ ‫المنقلة‬ ‫فى‬: ‫بحيث‬
‫ق‬(‫ال‬‫ا‬‫م‬‫حـ‬)=60ْْ
**‫عند‬ ‫الفرجار‬ ‫بسن‬ ‫نركز‬‫م‬‫طولها‬ ‫وبفتحة‬‫م‬‫ا‬‫ولتكن‬ ‫نقطة‬ ‫فى‬ ‫يقطع‬ ً‫ا‬‫قوس‬ ‫نرسم‬‫ا‬/
‫ا‬/
‫م‬ //
‫ا‬
‫ا‬‫م‬
‫ا‬/
‫ب‬
‫ب‬/
60
ْْ
60
ْْ
‫م‬‫ا‬
‫م‬‫ا‬‫م‬
‫حـ‬‫حـ‬
‫حـ‬
‫م‬
‫حـ‬‫حـ‬

10. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫فتكون‬‫ا‬/
‫صورة‬ ‫هى‬‫ا‬‫حول‬ ‫بالدوران‬‫م‬‫قياسها‬ ‫بزاوية‬60ْْ
‫ب‬ ‫إليجاد‬ ‫الخطوات‬ ‫نفس‬ ‫نتبع‬ ‫بالمثل‬ **/
‫ب‬ ‫صورة‬
‫فتكون‬ ‫نرسم‬ **‫المطلوب‬ ‫بالدوران‬ ‫صورة‬ ‫هى‬
‫؟‬ ‫تالحظ‬ ‫ماذا‬
( ‫تدريب‬1):
: ‫التالى‬ ‫الجدول‬ ‫أكمل‬
‫النقطة‬
) ‫و‬ ( ‫األصل‬ ‫نقطة‬ ‫حول‬ ‫بالدوران‬ ‫النقطة‬ ‫صورة‬
00ْْ‫أ؛‬–۲07
ْْ
180ْْ‫أ؛‬–
180ْْ
۲07ْ360ْْ–00ْْ
(3،4)(–4،3)(–3،–4)(3،–4)(3،4)(3،–4)
(1،–5)
(–۲،3)
(–3،–1)
(0،4)
(4،۲)
‫الدوران‬ ‫خواص‬‫فى‬: ‫المستوى‬
(1‫الدوران‬ )‫المستقيمة‬ ‫القطع‬ ‫أطوال‬ ‫على‬ ‫يحافظ‬
(۲‫الدوران‬ )‫الزوايا‬ ‫قياسات‬ ‫على‬ ‫يحافظ‬
(3‫الدوران‬ )‫ي‬‫التوازى‬ ‫على‬ ‫حافظ‬
(4‫الدوران‬ )‫البينية‬ ‫على‬ ‫يحافظ‬
: ‫أن‬ ‫كما‬‫الدوران‬‫الهندسى‬ ‫الشكل‬ ‫لرؤوس‬ ‫الدوارنى‬ ‫الترتيب‬ ‫على‬ ‫يحافظ‬
( ‫تدريب‬۲):
‫ا‬//‫ا‬

11. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ب‬‫حـ‬‫مركزه‬ ‫منتظم‬ ‫سداسى‬ ‫و‬ ‫هـ‬ ‫ء‬‫م‬: ‫يأتى‬ ‫ما‬ ‫أكمل‬
(1)‫صورة‬∆‫ب‬‫م‬‫حول‬ ‫بالدوران‬ ‫حـ‬‫م‬‫قياسها‬ ‫بزاوية‬60ْْ
‫هى‬0000
(۲‫صورة‬ )∆‫م‬‫حول‬ ‫بالدوران‬ ‫ء‬ ‫حـ‬‫م‬‫قياسها‬ ‫بزاوية‬1۲7ْْ
‫هى‬0000
(3)∆‫م‬‫صورة‬ ‫ء‬ ‫هـ‬∆0000‫حول‬ ‫بالدوران‬‫م‬‫بزا‬‫قياسها‬ ‫وية‬–1۲7ْْ
(4‫يحول‬ ‫الذى‬ ‫الدوران‬ )∆‫م‬‫ا‬‫إلى‬ ‫ب‬∆‫م‬‫هو‬ ‫و‬ ‫هـ‬0000
( ‫تدريب‬3):
‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫مستوى‬ ‫فى‬ :∆‫ا‬‫حيث‬ ‫حـ‬ ‫ب‬‫ا‬( =1،0( = ‫ب‬ ، )۲،3)
( = ‫حـ‬ ،4،۲)‫صورة‬ : ‫أوجد‬ ‫ثم‬∆‫ا‬‫حول‬ ‫بالدوران‬ ‫حـ‬ ‫ب‬: ‫األصل‬ ‫نقطة‬
‫قياسها‬ ‫بزاوية‬00ْ‫قياسها‬ ‫بزاوية‬ ،180ْْ
‫ال‬‫حلـــــــــــــــــــ‬
‫تمارين‬
(1)‫إرسم‬∆‫ا‬‫حـ‬ ‫ب‬‫ضلعه‬ ‫طول‬ ‫حيث‬ ‫األضالع‬ ‫المتساوى‬4‫فى‬ ‫باإلنعكاس‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ ‫سم‬
‫؟‬ ‫الناتج‬ ‫الشكل‬ ‫إسم‬ ‫ما‬ ‫وأذكر‬ ،
(۲)‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫نظام‬ ‫فى‬∆( = ‫ب‬ ، ‫األصل‬ ‫نقطة‬ ‫و‬ ‫حيث‬ ‫حـ‬ ‫ب‬ ‫و‬3،0( = ‫حـ‬ ، )3،4)
‫؟‬ ‫الناتج‬ ‫الشكل‬ ‫إسم‬ ‫ما‬ ‫وأذكر‬ ، ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورته‬ ‫إرسم‬ ‫ثم‬
(3)‫كانت‬ ‫إذا‬‫ا‬h‫ب‬ ، ‫ل‬ ‫لمستقيم‬g‫وكانت‬ ، ‫ل‬ ‫للمستقيم‬‫ا‬/
‫صورة‬‫ا‬‫فى‬ ‫باإلنعكاس‬
‫وكان‬ ، ‫ل‬ ‫المستقيم‬‫ا‬= ‫ب‬۲‫طول‬ ‫وحدة‬ ‫س‬،‫ا‬/
+ ‫س‬ = ‫ب‬3‫طول‬ ‫أوجد‬ ‫طول‬ ‫وحدة‬
‫ا‬
‫م‬
‫ب‬
‫حـ‬‫ء‬
‫هـ‬
‫و‬
60ْْ
‫س‬‫س‬/
‫ص‬
‫ص‬/
–3
–۲
–1
۲
3
4
1
–4
1–3 –۲ –1 0 3 4۲–4
‫ا‬‫ب‬
‫ا‬‫ب‬

12. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(4‫هـ‬ ‫صورة‬ ‫حـ‬ ‫وكانت‬ ، ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫النقطة‬ ‫صورة‬ ‫ب‬ ‫النقطة‬ ‫كانت‬ ‫إذا‬ )
( = ‫هـ‬ ‫حيث‬ ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬۲،3‫ب‬ ‫النقطة‬ ‫إحداثى‬ ‫أوجد‬ )
(5)‫إحداثى‬ ‫نظام‬ ‫فى‬‫إرسم‬ ‫متعامد‬‫المربع‬‫ا‬‫حـ‬ ‫ب‬‫حيث‬ ‫ء‬‫ا‬( =1،1( = ‫ب‬ ، )4،۲)
( = ‫حـ‬ ،3،5( = ‫ء‬ ، )0،4: ‫باإلنتقال‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ )
) ‫ص‬ ، ‫س‬ (←‫س‬ (–1‫ص‬ ،+1)‫باإلنتقال‬ ،‫ا‬‫ب‬‫اإلنتقال‬ ‫هذا‬ ‫قاعدة‬ ً‫ا‬‫مبين‬ ‫إتجاه‬ ‫فى‬
(6)‫المربع‬ ‫إرسم‬‫ا‬‫حـ‬ ‫ب‬‫ضل‬ ‫طول‬ ‫ء‬‫عه‬3‫باإلنتقال‬ ‫صورته‬ ‫إرسم‬ ‫ثم‬ ‫طول‬ ‫وحدة‬‫ا‬‫ب‬‫إتجاه‬ ‫فى‬
‫؟‬ ‫الناتج‬ ‫الشكل‬ ‫إسم‬ ‫ما‬ ‫فأذكر‬ ‫بصورتها‬ ‫نقطة‬ ‫كل‬ ‫وصلت‬ ‫وإذا‬ ،
(7)‫ب‬ ‫عين‬ ‫ثم‬ ‫إرسم‬/
‫حول‬ ‫بدوران‬ ‫ب‬ ‫صورة‬‫ا‬‫قياسها‬ ‫بزاوية‬60ْ: ‫كان‬ ‫إذا‬ ‫و‬ ،
‫ا‬( = ‫ب‬3‫س‬–10، ‫سم‬ )‫ا‬/
+ ‫س‬ ( = ‫ب‬۲‫س‬ )‫طول‬ ‫فأوجد‬ ‫م‬
(8)‫قطرها‬ ‫نصف‬ ‫طول‬ ‫دائرة‬ ‫إرسم‬3‫عن‬ ‫يبعد‬ ‫الذى‬ ‫ل‬ ‫المستقيم‬ ‫فى‬ ‫باإلنعكاس‬ ‫صورتها‬ ‫إرسم‬ ‫ثم‬ ‫سم‬
‫مركزها‬5‫سم‬
(0)‫ا‬‫حـ‬ ‫ب‬‫فيه‬ ‫معين‬ ‫ء‬‫ا‬( =۲،–۲( = ‫ب‬ ، )–1،–1( = ‫ء‬ ، )1،1‫الرسم‬ ‫من‬ ‫عين‬ )
‫باإل‬ ‫المعين‬ ‫صورة‬ ‫أوجد‬ ‫ثم‬ ‫حـ‬ ‫نقطة‬ ‫إحداثى‬‫السينات‬ ‫محور‬ ‫فى‬ ‫نعكاس‬
(10‫بإستخدام‬ )‫الشكل‬ ‫صورة‬ ‫أوجد‬ ‫المتعامدة‬ ‫التربيعية‬ ‫الشبكة‬‫ا‬‫حـ‬ ‫ب‬: ‫باإلنتقال‬ ‫ء‬
) ‫ص‬ ، ‫س‬ (←‫س‬ (+3‫ص‬ ،+1)‫حيث‬‫ا‬( =–1،۲( = ‫ب‬ ، )–1،–3)
= ‫حـ‬ ،(–3،–3)= ‫ء‬ ،(–3،۲)‫أذ‬ ‫بصورتها‬ ‫نقطة‬ ‫كل‬ ‫وصلت‬ ‫وإذا‬ ،‫إسم‬ ‫كر‬‫الناتج‬ ‫الشكل‬
(11)‫المربع‬ ‫إرسم‬‫ا‬‫حـ‬ ‫ب‬‫ضلعه‬ ‫طول‬ ‫ء‬4: ‫صورته‬ ‫أوجد‬ ‫ثم‬ ‫سم‬
‫باإلنتقال‬‫ا‬‫مسافة‬ ‫باإلنتقال‬ ‫صورته‬ ‫وكذا‬ ، ‫إتجاه‬ ‫فى‬ ‫حـ‬6‫إتجاه‬ ‫فى‬ ‫سم‬
(1۲)‫المتعامدة‬ ‫التربيعية‬ ‫شبكة‬ ‫على‬‫إرسم‬∆‫ا‬‫حـ‬ ‫ب‬‫حيث‬‫ا‬( =1،۲( = ‫ب‬ ، )4،1)
( = ‫حـ‬ ،3،4: ‫األصل‬ ‫نقطة‬ ‫حول‬ ‫بالدوران‬ ‫صورته‬ ‫إرسم‬ ‫ثم‬ )
‫قياسها‬ ‫بزاوية‬ **00ْ‫قياسها‬ ‫بزاوية‬ **180ْْ
(13)‫إرسم‬∆‫ا‬‫حـ‬ ‫ب‬‫ضلعه‬ ‫طول‬ ‫حيث‬ ‫األضالع‬ ‫المتساوى‬3: ‫صورته‬ ‫أوجد‬ ‫ثم‬ ‫سم‬
‫حول‬ ‫بالدوران‬ **‫ا‬‫قياسها‬ ‫بزاوية‬180‫حول‬ ‫بالدوران‬ ** ْْ‫ب‬‫قياسها‬ ‫بزاوية‬60ْْ
(14)‫ا‬‫حـ‬ ‫ب‬‫هـ‬ ، ‫مستطيل‬ ‫ء‬g‫صورة‬ ‫أوجد‬ ،∆‫ا‬‫ب‬‫مسافة‬ ‫هـ‬∆‫ا‬‫إتجاه‬ ‫فى‬ ‫ء‬
‫ا‬‫ب‬
‫ا‬‫حـ‬
‫ا‬‫ب‬
‫ا‬‫ب‬
‫ا‬‫حـ‬‫ب‬‫حـ‬
‫ا‬‫ء‬‫ا‬‫ء‬

13. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫هـ‬ ‫النقطة‬ ‫كانت‬ ‫وإذا‬ ،/
‫هـ‬ ‫حـ‬ ‫ب‬ ‫الشكل‬ ‫أن‬ ‫فبرهن‬ ‫اإلنتقال‬ ‫بهذا‬ ‫هـ‬ ‫النقطة‬ ‫صورة‬/
‫هـ‬
‫أضالع‬ ‫متوازى‬
(15)‫إرسم‬∆‫ا‬‫ب‬‫حـ‬‫فيه‬‫ا‬( =6،4)( = ‫ب‬ ،3،4( = ‫حـ‬ ، )6،7‫أوجد‬ ‫ثم‬ )‫ب‬/
‫حـ‬ ، ‫فى‬ ‫باإلنعكاس‬ ‫ب‬ ‫صورة‬/
‫نقطة‬ ‫فى‬ ‫باإلنعكاس‬ ‫حـ‬ ‫صورة‬‫ا‬‫الشكل‬ ‫أن‬ ‫برهن‬ ،
‫حـ‬/
‫ب‬ ‫حـ‬ ‫ب‬/
‫يحول‬ ‫الذى‬ ‫اإلنتقال‬ ‫عين‬ ، ‫مربع‬‫إلى‬
(16‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫نظام‬ ‫فى‬ )‫المربع‬‫ا‬‫حـ‬ ‫ب‬‫حيث‬ ‫ء‬‫ا‬( =0،۲( = ‫ب‬ ، )–5،0)
( = ‫حـ‬ ،–3،–5( = ‫ء‬ ، )۲،–3‫صورته‬ ‫أوجد‬ )‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬
‫مساحته‬ ، ‫ضلعه‬ ‫طول‬ ‫أوجد‬ ‫ثم‬
(17‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫نظام‬ ‫فى‬ )‫المربع‬‫ا‬‫حـ‬ ‫ب‬‫حيث‬ ‫ء‬‫ا‬( =۲،3( = ‫ب‬ ، )۲،–1)
‫صورته‬ ‫أوجد‬ ‫ثم‬‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬‫؟‬ ‫تالحظ‬ ‫ماذا‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫بإنعكاس‬ ً‫ا‬‫متبوع‬
(18‫إرسم‬ ‫متعامد‬ ‫إحداثى‬ ‫نظام‬ ‫فى‬ )‫المستطيل‬‫ا‬‫حـ‬ ‫ب‬‫حيث‬ ‫ء‬‫ا‬( =۲،۲( = ‫ب‬ ، )–3،۲)
‫يساوى‬ ‫عرضه‬ ،3‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫طول‬ ‫وحدات‬‫رسم‬ ‫يمكن‬ ‫حالة‬ ‫كم‬‫؟‬ ‫ها‬
(10( ‫حـ‬ ‫كانت‬ ‫إذا‬ )–3،–1، ‫الصادات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬ ‫ب‬ ‫صورة‬ ‫هى‬ )‫ا‬‫ب‬ ‫صورة‬ ‫هى‬
‫يجعل‬ ‫الذى‬ ‫اإلنتقال‬ ‫فأوجد‬ ‫السينات‬ ‫محور‬ ‫فى‬ ‫باإلنعكاس‬‫ا‬‫حـ‬ ‫صورة‬
‫التشابه‬
‫مضلعين‬ ‫تشابه‬:
‫إذا‬ ‫متشابهان‬ ‫أنهما‬ )‫األضالع‬ ‫من‬ ‫العدد‬ ‫نفس‬ ‫لمضلعين(لهما‬ ‫يقال‬‫تحقق‬‫الشر‬: ‫معا‬ ‫اآلتيين‬ ‫طين‬
‫متساوية‬ ‫المتناظرة‬ ‫زواياهما‬ ‫قياسات‬ ) ً‫ال‬‫أو‬ (‫متناسبة‬ ‫المتناظرة‬ ‫أضالعهما‬ ‫أطوال‬ ) ً‫ا‬‫ثاني‬ (
‫مالحظة‬( ‫الرمز‬ ‫يستخدم‬ :R‫التشابه‬ ‫عن‬ ‫للتعبير‬ )
: ‫المقابل‬ ‫الشكل‬ ‫ففى‬
‫ل‬ ‫ع‬ ‫ص‬ ‫س‬ ‫المضلع‬ : ‫كان‬ ‫إذا‬R‫المضلع‬‫و‬ ‫هـ‬ ‫ء‬ ‫حـ‬
‫ا‬‫حـ‬
‫حـ‬/
‫ب‬/
‫حـ‬‫ب‬
‫ح‬
‫ـ‬

14. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
: ‫فإن‬‫ق‬(‫ال‬= ) ‫س‬‫ق‬(‫ال‬‫حـ‬)
،‫ق‬(‫ال‬‫ص‬= )‫ق‬(‫ال‬‫ء‬)
،‫ق‬(‫ال‬‫ع‬= )‫ق‬(‫ال‬‫هـ‬)
،‫ق‬(‫ال‬‫ل‬= )‫ق‬(‫ال‬‫و‬)
: ً‫ا‬‫أيض‬===‫ثابت‬ ‫مقدار‬ =
‫تدريب‬:
‫المضلع‬ : ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫هـ‬ ‫ء‬ ‫حـ‬ ‫ب‬R‫ل‬ ‫ع‬ ‫ص‬ ‫س‬ ‫المضلع‬‫م‬
: ‫أطوال‬ ‫أوجد‬ ‫المبينة‬ ‫األطوال‬ ‫بإستخدام‬
‫س‬، ‫ل‬ ‫ع‬ ، ‫ص‬‫ل‬‫م‬،‫ا‬‫هـ‬
‫الحلـــــــــــــــ‬
A‫المضلع‬‫ا‬‫هـ‬ ‫ء‬ ‫حـ‬ ‫ب‬R‫ل‬ ‫ع‬ ‫ص‬ ‫س‬ ‫المضلع‬‫م‬
B= =0000=0000=0000
B0000==0000=0000=0000
B= ‫ص‬ ‫س‬0000= ‫ل‬ ‫ع‬ ،0000
B= ‫م‬ ‫ل‬0000،‫ا‬= ‫هـ‬0000
‫هامة‬ ‫مالحظات‬:
(1‫المتناظرة‬ ‫رؤوسهما‬ ‫ترتيب‬ ‫بنفس‬ ‫المتشابهين‬ ‫المضلعين‬ ‫كتابة‬ ‫يجب‬ )
‫المضلع‬ ‫كان‬ ‫فإذا‬‫ا‬‫هـ‬ ‫ء‬ ‫حـ‬ ‫ب‬R‫ل‬ ‫ع‬ ‫ص‬ ‫س‬ ‫المضلع‬‫م‬: ‫فإن‬
‫الرأس‬‫ا‬‫وهكذا‬ .... ‫ص‬ ‫الرأس‬ ‫يناظر‬ ‫ب‬ ‫الرأس‬ ، ‫س‬ ‫الرأس‬ ‫يناظر‬
(۲‫إذا‬ )‫نس‬ ‫فإننا‬ ‫مضلعان‬ ‫تشابه‬‫متساوية‬ ‫المتناظرة‬ ‫زواياهما‬ ‫قياسات‬ ** : ‫أن‬ ‫تنتج‬
‫متناسبة‬ ‫المتناظرة‬ ‫أضالعهما‬ ‫أطوال‬ **
‫ا‬
‫ء‬
‫ب‬
‫ح‬
‫ـ‬
‫ء‬
‫ه‬
‫ـ‬
‫س‬
‫ص‬
‫ع‬‫ل‬
‫م‬
4‫سم‬
8‫سم‬
14‫سم‬
10‫سم‬
11‫سم‬
‫ص‬ ‫س‬
‫ا‬‫ب‬
‫ع‬ ‫ص‬
‫حـ‬ ‫ب‬
4
8
3‫سم‬
‫ء‬‫ه‬
‫ـ‬
‫س‬
‫ص‬
‫ل‬
‫ع‬
‫و‬

15. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(3‫اآلخر‬ ‫دون‬ ‫أحدهما‬ ‫توافر‬ ‫يكفى‬ ‫وال‬ ً‫ا‬‫مع‬ ‫الشرطين‬ ‫توافر‬ ‫يجب‬ ‫مضلعان‬ ‫يتشابه‬ ‫لكى‬ )
(4‫بينما‬ ‫متشابهان‬ ‫المتطابقان‬ ‫المضلعان‬ )‫المتشابهان‬ ‫المضلعان‬ ‫يكون‬ ‫أن‬ ‫الضرورى‬ ‫من‬ ‫ليس‬
‫متطابقين‬
(5‫متشابهان‬ ‫لثالث‬ ‫المشابهان‬ ‫المضلعان‬ )
(1‫متشابهين‬ ‫يكونان‬ ‫األضالع‬ ‫عدد‬ ‫نفس‬ ‫لهما‬ ‫منتظمين‬ ‫مضلعين‬ ‫أى‬ )
(7‫مقياس‬ ‫أو‬ ‫التكبير‬ ‫بنسبة‬ ‫األضالع‬ ‫أطوال‬ ‫بين‬ ‫الثابتة‬ ‫النسبة‬ ‫تسمى‬ )‫الرسم‬
= ‫النسبة‬ ‫هذه‬ ‫كانت‬ ‫وإذا‬ ،1‫يتطابقان‬ ‫المضلعين‬ ‫فإن‬
‫؟‬ ‫لماذا‬ ‫و‬ ‫؟‬ ‫والمستطيل‬ ‫المربع‬ ‫يتشابه‬ ‫هل‬ : ‫تدريب‬
‫والمعين‬ ‫المربع‬ ‫يتشابه‬ ‫هل‬‫؟‬ ‫لماذا‬ ‫و‬ ‫؟‬
‫المثلثات‬ ‫تشــــابـــه‬
: ‫الشرطين‬ ‫أحد‬ ‫توفر‬ ‫إذا‬ ‫المثلثان‬ ‫يتشابه‬
‫الزوا‬ : ً‫ال‬‫أو‬‫القياس‬ ‫فى‬ ‫متساوية‬ ‫المتناظرة‬ ‫يا‬‫الطول‬ ‫فى‬ ‫متساوية‬ ‫المتناظرة‬ ‫األضالع‬ : ً‫ا‬‫ثاني‬
: ‫الشكل‬ ‫ففى‬: ‫الشكل‬ ‫ففى‬
A//A==3
B∆‫س‬‫ع‬ ‫ص‬R∆‫س‬‫هـ‬ ‫ء‬،==3،=
3
9=3
: ‫ألن‬‫ال‬‫المثلثين‬ ‫بين‬ ‫مشتركة‬ ‫س‬B∆‫س‬‫ع‬ ‫ص‬R∆‫هـ‬ ‫ء‬‫و‬
‫ء‬‫ه‬
‫ـ‬
‫س‬
‫ص‬‫ع‬
‫هـ‬ ‫ء‬‫حـ‬ ‫ب‬
‫ء‬
‫ه‬
‫ـ‬
‫س‬
‫ص‬‫ع‬‫و‬
6‫سم‬0‫سم‬
1۲‫سم‬
۲‫سم‬
3‫سم‬
4‫سم‬ ۲
6
4
1۲

16. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
،‫ق‬(‫ال‬‫ص‬= )‫ق‬(‫ال‬‫هـ‬ ‫ء‬ ‫س‬)‫؟‬ ‫لماذا‬‫المثلثي‬ ‫تشابه‬ ‫ومن‬ ،: ‫نستنتج‬ ‫ن‬
‫ق‬(‫ال‬‫ع‬= )‫ق‬(‫ال‬‫هـ‬ ‫س‬‫ء‬)‫؟‬ ‫لماذا‬‫ق‬(‫ال‬‫س‬= )‫ق‬(‫ال‬‫ء‬)
: ‫نستنتج‬ ‫المثلثين‬ ‫تشابه‬ ‫ومن‬ ،،‫ق‬(‫ال‬‫ص‬= )‫ق‬(‫ال‬‫هـ‬)
==،‫ق‬(‫ال‬‫ع‬= )‫ق‬(‫ال‬‫و‬)
‫مالحظة‬:‫يتشاب‬‫اآلخر‬ ‫من‬ ‫زاويتين‬ ‫قياس‬ ‫أحدهما‬ ‫من‬ ‫زاويتين‬ ‫قياس‬ ‫ساوى‬ ‫إذا‬ ‫المثلثان‬ ‫ه‬
: ‫كان‬ ‫إذا‬ : ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫ق‬(‫ال‬= ) ‫ء‬‫ق‬(‫ال‬‫ا‬)
‫ق‬(‫ال‬= ) ‫هـ‬‫ق‬(‫ال‬) ‫ب‬
: ‫فإن‬‫ق‬(‫ال‬= ) ‫و‬‫ق‬(‫ال‬) ‫حـ‬‫؟‬ ‫لماذا‬
= ،=
‫خاصة‬ ‫حاالت‬:
(1‫متشابهان‬ ‫األضالع‬ ‫المتساويا‬ ‫المثلثان‬ )
(2‫إذا‬ ‫الزاوية‬ ‫القائما‬ ‫المثلثان‬ ‫يتشابه‬ )‫قياس‬ ‫أحدهما‬ ‫فى‬ ‫الحادتين‬ ‫الزاويتين‬ ‫إحدى‬ ‫قياس‬ ‫ساوى‬
‫الحاد‬ ‫الزاويتين‬ ‫إحدى‬‫فى‬ ‫تين‬‫اآلخر‬
(3‫إذا‬ ‫الساقين‬ ‫المتساويا‬ ‫المثلثان‬ ‫يتشابه‬ )‫قياس‬ ‫أحدهما‬ ‫فى‬ ‫القاعدة‬ ‫زاويتى‬ ‫إحدى‬ ‫قياس‬ ‫ساوى‬
‫فى‬ ‫القاعدة‬ ‫زاويتى‬ ‫إحدى‬‫اآلخر‬
‫ملحوظة‬:‫المثلث‬ ‫كتابة‬ ‫يجب‬‫المتناظرة‬ ‫رؤوسهما‬ ‫ترتيب‬ ‫بنفس‬ ‫المتشابهين‬ ‫ين‬
‫مالحظة‬:‫إذا‬‫ا‬ ‫المثلث‬ ‫فى‬ ‫القائمة‬ ‫رأس‬ ‫من‬ ‫رسم‬‫إلى‬ ‫المثلث‬ ‫إنقسم‬ ‫الوتر‬ ‫على‬ ‫عمود‬ ‫الزاوية‬ ‫لقائم‬
‫المثلث‬ ‫يشابه‬ ‫وكالهما‬ ‫متشابهين‬ ‫مثلثين‬‫األصلى‬
‫ف‬‫ف‬: ‫المقابل‬ ‫الشكل‬ ‫ى‬
‫ا‬
‫ء‬
‫ب‬‫ح‬
‫ـ‬
‫ء‬
‫ه‬
‫ـ‬
‫و‬
‫هـ‬ ‫ء‬
‫ا‬‫ب‬
‫و‬ ‫هـ‬
‫حـ‬ ‫ب‬
‫ء‬ ‫و‬
‫حـ‬‫ا‬
‫ا‬
‫ء‬

17. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
∆‫ا‬‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬ ‫ب‬‫ا‬،‫ا‬‫ء‬M‫حـ‬ ‫ب‬
: ‫فإن‬∆‫ا‬‫حـ‬ ‫ب‬R∆‫ب‬ ‫ء‬‫ا‬R∆‫ء‬‫ا‬‫حـ‬
: ‫نجد‬ ‫ذلك‬ ‫من‬ ‫و‬
=B(‫ا‬) ‫ب‬
۲
‫ب‬ ‫ء‬ =×‫حـ‬ ‫ب‬
( ،‫ا‬) ‫حـ‬
۲
‫حـ‬ ‫ء‬ =×‫حـ‬ ‫ب‬
( ،‫ا‬) ‫ء‬
۲
‫حـ‬ ‫ء‬ =×‫ب‬ ‫ء‬‫ء‬ ،‫ا‬×= ‫حـ‬ ‫ب‬‫ا‬‫ب‬×‫ا‬‫حـ‬
‫تدريب‬:
( ‫ق‬ ، ‫مثلث‬ ‫و‬ ‫هـ‬ ‫ء‬ ‫الشكل‬ ‫فى‬‫ال‬( ‫ق‬ = ) ‫و‬‫ال‬) ‫ص‬ ‫س‬ ‫ء‬
= ‫س‬ ‫ء‬ ،5= ‫و‬ ‫ص‬ ، ‫سم‬10= ‫ص‬ ‫ء‬ ، ‫سم‬3‫سم‬
‫هـ‬ ‫س‬ ‫طول‬ ‫أوجد‬
‫الحلــــــــــــــــــــــ‬
∆∆: ‫فيهما‬ ‫س‬ ‫ص‬ ‫ء‬ ، ‫و‬ ‫هـ‬ ‫ء‬
‫ق‬(‫ال‬= ) ‫و‬‫ق‬(‫ال‬0000، )‫ال‬‫ء‬0000
B∆‫و‬ ‫هـ‬ ‫ء‬R∆0000B=0000=0000
B= ‫هـ‬ ‫ء‬0000‫سم‬B= ‫هـ‬ ‫س‬0000
‫تدريب‬:
= ‫و‬ ‫ء‬ ‫كان‬ ‫إذا‬ ‫الشكل‬ ‫فى‬1۲= ‫هـ‬ ‫ء‬ ، ‫سم‬10، ‫سم‬
= ‫و‬ ‫هـ‬8= ‫هـ‬ ‫س‬ ، ‫سم‬4= ‫و‬ ‫ص‬ ، ‫سم‬7، ‫سم‬
= ‫ص‬ ‫س‬4‫أثبت‬ ‫سم‬: ‫أن‬
∆‫و‬ ‫هـ‬ ‫ء‬R∆‫س‬ ‫ص‬ ‫ء‬
‫الحلــــــــــــــــــــــ‬
‫ء‬
‫ب‬ ‫ء‬
‫ا‬‫ب‬
‫ا‬‫ب‬
‫حـ‬ ‫ب‬
‫ء‬
‫ه‬
‫ـ‬
‫س‬
‫ص‬
‫و‬
‫ص‬ ‫ء‬
‫هـ‬ ‫ء‬
*
*
‫ء‬
‫ه‬
‫ـ‬
‫س‬
‫ص‬
‫و‬

18. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
∆∆: ‫فيهما‬ ‫س‬ ‫ص‬ ‫ء‬ ، ‫و‬ ‫هـ‬ ‫ء‬
= ،0000= ،0000= ،0000
B0000=0000=0000
B∆‫و‬ ‫هـ‬ ‫ء‬R∆0000
‫مالحظة‬‫متناظرين‬ ‫ضلعين‬ ‫أى‬ ‫طولى‬ ‫بين‬ ‫النسبة‬ ‫تساوى‬ ‫متشابهين‬ ‫مضلعين‬ ‫محيطى‬ ‫بين‬ ‫النسبة‬ :
‫تدريب‬:
‫فيهما‬ ‫متناظرين‬ ‫ضلعين‬ ‫طولى‬ ‫بين‬ ‫النسبة‬ ‫متشابهان‬ ‫مضلعان‬1:3‫بين‬ ‫النسبة‬ ‫أوجد‬
‫محيطيهما‬
‫الحلــــــــــــــــــــــ‬
A‫المضلعان‬‫متشابهان‬،‫فيهما‬ ‫متناظرين‬ ‫ضلعين‬ ‫طولى‬ ‫بين‬ ‫النسبة‬1:3
B‫محيطيهما‬ ‫بين‬ ‫النسبة‬=0000
‫تمــــارين‬
(1‫أحدهما‬ ‫في‬ ‫زاوية‬ ‫قياس‬ ‫الزاوية‬ ‫قائما‬ ‫مثلثان‬ : ‫أكمل‬ )4۲ْ‫اآلخر‬ ‫في‬ ‫زاوية‬ ‫وقياس‬48ْْ
‫المثلثان‬ ‫كان‬0000
(۲‫مت‬ ‫مثلثان‬ : ‫أكمل‬ )‫أحدهما‬ ‫رأس‬ ‫زاوية‬ ‫قياس‬ ‫الساقين‬ ‫ساويا‬70ْ‫اآلخر‬ ‫في‬ ‫زاوية‬ ‫وقياس‬40ْْ
‫فيكون‬0000
(3‫محيطيهما‬ ‫بين‬ ‫النسبة‬ ‫متشابهان‬ ‫مضلعان‬ : ‫أكمل‬ )4:7‫ضلعين‬ ‫أى‬ ‫طولى‬ ‫بين‬ ‫النسبة‬ ‫تكون‬
= ‫فيهما‬ ‫متناظرين‬0000
(4‫أكمل‬ ):‫بين‬ ‫النسبة‬ ‫متشابهان‬ ‫مضلعان‬‫ط‬‫فيهما‬ ‫متناظرين‬ ‫ضلعين‬ ‫أى‬ ‫ولى‬5:0‫بين‬ ‫النسبة‬ ‫تكون‬
‫محيطيهما‬000
(5: ‫أكمل‬ )‫زواياه‬ ‫إحدى‬ ‫قياس‬ ‫الزاوية‬ ‫منفرج‬ ‫أحدهما‬ ‫متشابهين‬ ‫مثلثان‬40ْ‫متساوى‬ ‫اآلخر‬ ‫والمثلث‬
= ‫المنفرجة‬ ‫الزاوية‬ ‫قياس‬ ‫فإن‬ ‫الساقين‬0000ْْ
‫ص‬ ‫ء‬
‫هـ‬ ‫ء‬
‫ء‬ ‫س‬
‫ء‬ ‫و‬
‫س‬ ‫ص‬
‫و‬ ‫هـ‬

19. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(6): ‫كان‬ ‫إذا‬∆‫ا‬‫حـ‬ ‫ب‬~∆‫ء‬‫و‬ ‫هـ‬،‫كان‬‫ا‬= ‫ب‬8= ‫هـ‬ ‫ء‬ ، ‫سم‬۲‫سم‬،‫ق‬(‫ال‬) ‫ب‬‫س‬ =ْْ
،‫ق‬(‫ال‬‫هـ‬)+ ‫س‬ ( =50‫التكبير‬ ‫نسبة‬ ، ‫بالدرجات‬ ‫س‬ ‫قيمة‬ ‫أوجد‬ ْ )
(7): ‫المقابل‬ ‫الشكل‬ ‫فى‬//،‫ا‬‫ب‬=15‫ه‬ ‫ء‬ ، ‫سم‬= ‫ـ‬5‫سم‬
= ‫حـ‬ ‫ء‬ ،4: ‫أن‬ ‫أثبت‬ ‫سم‬∆‫ا‬‫حـ‬ ‫ب‬~∆‫حـ‬ ‫ء‬ ‫هـ‬
‫أوجد‬ ‫ثم‬‫محيط‬‫ا‬‫حـ‬ ‫ب‬‫تجعل‬ ‫التى‬ ‫التكبير‬ ‫نسبة‬ ،∆‫حـ‬ ‫ء‬ ‫هـ‬‫صورة‬∆‫ا‬‫حـ‬ ‫ب‬
(8): ‫المقابل‬ ‫الشكل‬ ‫فى‬∆‫ا‬‫حـ‬ ‫ب‬~∆‫ء‬‫ا‬‫حـ‬
،‫ق‬(‫ال‬‫ا‬‫حـ‬ ‫ب‬)( =۲+ ‫س‬۲5ْ )
،‫ق‬(‫ال‬‫ء‬‫ا‬‫حـ‬)+ ‫(س‬ =40ْ )‫ب‬ ،= ‫حـ‬5‫سم‬
= ‫حـ‬ ‫ء‬ ،4‫طول‬ ، ‫بالدرجات‬ ‫س‬ ‫قيمة‬ ‫أوجد‬ ‫سم‬
(9): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ق‬(‫ال‬‫ا‬‫ء‬ ‫هـ‬)=‫ق‬(‫ال‬‫حـ‬)
،‫ا‬‫ء‬=۲‫سم‬،‫ا‬‫هـ‬=3= ‫حـ‬ ‫ء‬ ، ‫سم‬5‫سم‬
: ‫أن‬ ‫أثبت‬∆‫ا‬‫ء‬ ‫هـ‬~∆‫ا‬‫ب‬ ‫حـ‬‫طول‬ ‫أوجد‬ ‫ثم‬
(10)‫الش‬ ‫فى‬: ‫المقابل‬ ‫كل‬‫كان‬ ‫إذا‬‫ا‬= ‫ب‬8‫سم‬
،‫ا‬= ‫حـ‬6= ‫حـ‬ ‫ء‬ ، ‫سم‬3.6‫سم‬
‫كان‬ ،∆‫ا‬‫ب‬ ‫ء‬~∆‫ء‬ ‫حـ‬‫ا‬
‫من‬ ‫كل‬ ‫طول‬ ‫فأوجد‬،
(11): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫أضالع‬ ‫متوازى‬ ‫ء‬ ‫حـ‬ ‫ب‬
‫و‬g،‫بال‬} ‫هـ‬ { =
: ‫كان‬ ‫فإذا‬‫ا‬= ‫هـ‬ ‫ب‬ = ‫ب‬1۲= ‫حـ‬ ‫هـ‬ ، ‫سم‬8‫سم‬
‫أن‬ ‫أثبت‬∆‫ء‬‫حـ‬ ‫هـ‬~∆‫طول‬ ‫أوجد‬ ‫ثم‬ ‫ب‬ ‫هـ‬ ‫و‬
‫ا‬
‫ء‬
‫ب‬
‫ح‬
‫ـ‬ ‫ء‬‫ه‬
‫ـ‬
‫ا‬‫ب‬‫هـ‬ ‫ء‬
‫ا‬‫حـ‬
‫ا‬
‫ء‬
‫ب‬‫ح‬
‫ـ‬
‫ء‬
‫ا‬
‫ب‬
‫ه‬
‫ـ‬
‫ء‬
‫ح‬
‫ـ‬
*
*
‫ب‬‫ه‬‫ـ‬
‫ا‬
‫ء‬
‫ب‬ ‫ح‬
‫ـ‬
‫ء‬
‫ا‬‫ء‬‫ب‬‫ء‬
‫ا‬
‫ء‬
‫ب‬
‫ح‬
‫ـ‬
‫ء‬
‫و‬
‫ا‬‫ب‬‫ه‬
‫ـ‬
‫و‬‫ء‬‫ب‬‫حـ‬
‫ب‬‫و‬
‫ا‬
‫ء‬

20. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(1۲): ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫ا‬‫ب‬=10، ‫سم‬‫ا‬= ‫حـ‬5‫سم‬
= ‫حـ‬ ‫ب‬ ،۲5‫سم‬،‫ا‬= ‫ء‬۲4‫سم‬
‫أن‬ ‫أثبت‬∆‫ا‬‫ب‬‫حـ‬~∆‫ء‬ ‫ب‬‫ا‬// ،
(13): ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫ا‬= ‫ب‬14، ‫سم‬‫ا‬= ‫حـ‬6= ‫حـ‬ ‫هـ‬ = ‫هـ‬ ‫ب‬ ، ‫سم‬5‫سم‬
= ‫حـ‬ ‫ء‬ ،7= ‫هـ‬ ‫ء‬ ، ‫سم‬3‫سم‬
‫أن‬ ‫أثبت‬‫ا‬‫هـ‬ ‫ء‬ // ‫حـ‬
‫المساحات‬
‫أضالع‬ ‫متوازيى‬ ‫مساحتى‬ ‫تساوى‬
‫أن‬ ‫نعلم‬:
**‫متوازيين‬ ‫متقابلين‬ ‫ضلعين‬ ‫كل‬ ‫فيه‬ ‫رباعى‬ ‫شكل‬ ‫هو‬ ‫األضالع‬ ‫متوازى‬
: ‫األضالع‬ ‫متوازى‬ ‫خواص‬ **
(1‫الطول‬ ‫فى‬ ‫متساويين‬ ‫متقابلين‬ ‫ضلعين‬ ‫كل‬ )
(۲‫القي‬ ‫فى‬ ‫متساويتين‬ ‫متقابلتين‬ ‫زاويتين‬ ‫كل‬ )‫اس‬
(3‫اآلخر‬ ‫منهما‬ ‫كل‬ ‫ينصف‬ ‫القطران‬ )
‫األضالع‬ ‫متوازى‬ ‫من‬ ‫خاصة‬ ‫حاالت‬ ‫هى‬ ‫والمربع‬ ‫والمستطيل‬ ‫المعين‬ **
‫ثابت‬ ‫متوازيين‬ ‫مستقيمين‬ ‫كل‬ ‫بين‬ ‫البعد‬ **0000‫بيئتك‬ ‫من‬ ‫أمثلة‬ ‫أذكر‬ ، ‫لذلك‬ ‫مثال‬ ‫إرسم‬
‫األض‬ ‫متوازى‬ ‫إرتفاع‬‫الع‬:
‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫حـ‬ ‫ب‬‫أضالع‬ ‫متوازى‬ ‫ء‬
‫ا‬‫ء‬
‫و‬
‫حـ‬‫ب‬‫هـ‬ ‫ء‬‫حـ‬‫ب‬
‫هـ‬ ////
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫ب‬
‫ح‬
‫ـ‬
‫ء‬
‫ب‬‫ء‬‫ا‬‫حـ‬

21. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫وكان‬ ، ‫له‬ ‫قاعدة‬ ‫كانت‬ ‫إذا‬M
‫فيكون‬‫طول‬‫للقاعدة‬ ‫المناظر‬ ‫اإلرتفاع‬ ‫هو‬
‫بالمثل‬‫طول‬‫للقاعدة‬ ‫المناظر‬ ‫اإلرتفاع‬ ‫هو‬
‫مالحظة‬:
‫للقاعدة‬ ‫المناظر‬ ‫األضالع‬ ‫متوازى‬ ‫إرتفاع‬
ً‫ا‬‫مساوي‬ ‫يكون‬‫للقاعدة‬ ‫المناظر‬ ‫لإلرتفاع‬
‫ب‬ ‫ع‬ = ‫ص‬ ‫س‬ = ‫هـ‬ ‫ء‬ : ‫حيث‬
( ‫نظرية‬1):
‫مستق‬ ‫بين‬ ‫والمحصورين‬ ‫القاعدة‬ ‫فى‬ ‫المشتركين‬ ‫األضالع‬ ‫متوازيى‬ ‫سطحا‬‫متوازيين‬ ‫يمين‬
‫المساحة‬ ‫فى‬ ‫متساويان‬ ‫القاعدة‬ ‫هذه‬ ‫يحمل‬ ‫أحدهما‬
‫المعطيات‬:‫ا‬‫حـ‬ ‫ب‬‫أضالع‬ ‫متوازيا‬ ‫و‬ ‫حـ‬ ‫ب‬ ‫هـ‬ ، ‫ء‬
// ، ‫لهما‬ ‫مشتركة‬ ‫قاعدة‬ ،
‫المطلوب‬‫مساحة‬ : ‫أن‬ ‫إثبات‬ :‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ = ‫ء‬
‫و‬ ‫حـ‬ ‫ب‬ ‫هـ‬
‫البرهان‬:A∆‫صورة‬ ‫و‬ ‫حـ‬ ‫ء‬∆‫ا‬‫ب‬‫هـ‬
‫إتجاه‬ ‫فى‬ ‫حـ‬ ‫ب‬ ‫مسافة‬ ‫بإنتقال‬
B∆‫و‬ ‫حـ‬ ‫ء‬≡∆‫ا‬‫ب‬‫هـ‬
‫اإلنتقال‬ ‫ألن‬ "
" ‫قياسى‬ ‫تساوى‬
B‫الشكل‬ ‫مساحة‬‫ا‬‫حـ‬ ‫ب‬‫و‬–‫مساحة‬∆‫الشكل‬ ‫مساحة‬ = ‫و‬ ‫حـ‬ ‫ء‬‫ا‬‫حـ‬ ‫ب‬‫و‬–‫مساحة‬∆‫ا‬‫ب‬‫هـ‬
B‫مساحة‬‫ا‬‫حـ‬ ‫ب‬‫و‬ ‫حـ‬ ‫ب‬ ‫هـ‬ ‫مساحة‬ = ‫ء‬
‫ب‬‫حـ‬
‫هـ‬
‫هـ‬ ‫ء‬‫حـ‬‫ب‬
‫و‬ ‫ء‬‫ا‬‫ب‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫س‬
‫ص‬
‫ع‬
■
■ ■
■
‫حـ‬‫ب‬===
‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬ ‫هـ‬‫و‬
‫حـ‬‫ب‬‫ب‬‫حـ‬‫ا‬‫و‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬‫هـ‬‫و‬
‫ب‬‫حـ‬
‫ا‬
‫ب‬
‫ء‬ ‫هـ‬‫و‬

22. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫نت‬‫ي‬‫ج‬( ‫ة‬1):
‫متواز‬ ‫سطح‬ ‫مساحة‬‫المستطيل‬ ‫سطح‬ ‫مساحة‬ ‫تساوى‬ ‫األضالع‬ ‫ى‬
‫متوازيين‬ ‫مستقيمين‬ ‫بين‬ ‫معه‬ ‫والمحصور‬ ‫القاعدة‬ ‫فى‬ ‫معه‬ ‫المشترك‬
‫القاعدة‬ ‫هذه‬ ‫يحمل‬ ‫أحدهما‬
‫المستطيل‬ ‫مساحة‬ : ‫المقابل‬ ‫الشكل‬ ‫ففى‬‫ا‬‫حـ‬ ‫ب‬‫هـ‬ ‫حـ‬ ‫ب‬ ‫و‬ ‫مساحة‬ = ‫ء‬‫؟؟؟‬ ‫لماذا‬
‫نت‬‫ي‬‫ج‬( ‫ة‬۲):‫س‬ ‫مساحة‬‫قاعدته‬ ‫طول‬ = ‫األضالع‬ ‫متوازى‬ ‫طح‬×‫إرتفاعه‬
‫تدريب‬:‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫حـ‬ ‫ب‬‫أضالع‬ ‫متوازى‬ ‫ء‬
،M،M،= ‫هـ‬ ‫ء‬10‫سم‬
= ‫و‬ ‫ء‬ ،8= ‫حـ‬ ‫ب‬ ، ‫سم‬1۲‫سم‬
‫األضالع‬ ‫متوازى‬ ‫سطح‬ ‫مساحة‬ ‫أوجد‬‫ا‬‫حـ‬ ‫ب‬‫طول‬ ‫أحسب‬ ‫ثم‬ ‫ء‬
‫الحلــــــــــــــــ‬
‫طول‬ ‫فيكون‬ ‫األضالع‬ ‫لمتوازى‬ ‫قاعدة‬ ‫بإعتبار‬0000‫اإلرتفاع‬
B= ‫األضالع‬ ‫متوازى‬ ‫مساحة‬0000×0000=0000×0000=0000‫سم‬
۲
‫بإعتبار‬ ،0000‫طول‬ ‫فيكون‬ ‫األضالع‬ ‫لمتوازى‬ ‫قاعدة‬0000‫اإلرتفاع‬
B= ‫األضالع‬ ‫متوازى‬ ‫مساحة‬0000×0000
B0000=0000×0000B‫ا‬‫ب‬=0000=0000‫سم‬
‫تدريب‬:: ‫التالى‬ ‫الجدول‬ ‫إكمل‬
‫متوازى‬ ‫مساحة‬
‫األضالع‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
‫القاعدة‬ ‫طول‬‫المناظر‬ ‫إرتفاع‬ ‫طول‬
‫للقاعدة‬
‫القاعدة‬ ‫طول‬‫المناظر‬ ‫إرتفاع‬ ‫طول‬
‫للقا‬‫عدة‬
5‫سم‬6‫سم‬3‫سم‬
60‫سم‬
۲
10‫سم‬1۲‫سم‬
30‫سم‬8‫سم‬15‫سم‬
18‫سم‬8‫سم‬0‫سم‬
‫نت‬‫ي‬‫ج‬( ‫ة‬3):‫مس‬ ‫بين‬ ‫المحصورة‬ ‫األضالع‬ ‫متوازيات‬‫تقيمين‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫و‬
‫هـ‬ ‫ء‬‫حـ‬‫ب‬
‫ا‬‫ب‬
‫و‬ ‫ء‬‫ا‬‫حـ‬
‫ب‬
‫حـ‬‫ب‬
‫ا‬‫ء‬‫و‬‫س‬‫ل‬ ‫ز‬
‫حـ‬‫ب‬‫حـ‬‫ب‬‫ا‬‫ب‬‫ا‬‫ب‬

23. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫المستقيمين‬ ‫هذين‬ ‫على‬ ‫التى‬ ‫وقواعدها‬ ‫متوازيين‬
‫متساوية‬‫متساوية‬ ‫مساحاتها‬ ‫تكون‬ ‫الطول‬ ‫فى‬
// ‫كان‬ ‫إذا‬ : ‫المقابل‬ ‫الشكل‬ ‫ففى‬
‫ع‬ ‫ص‬ = ‫ر‬ ‫هـ‬ = ‫حـ‬ ‫ب‬ ،: ‫فإن‬
‫مساحة‬‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ = ‫و‬ ‫ز‬ ‫ر‬ ‫هـ‬ ‫مساحة‬ = ‫ء‬‫ل‬ ‫ع‬ ‫ص‬ ‫س‬
‫نت‬‫ي‬‫ج‬( ‫ة‬4):‫تساوى‬ ‫المثلث‬ ‫سطح‬ ‫مساحة‬‫متوازى‬ ‫سطح‬ ‫مساحة‬ ‫نصف‬
‫بين‬ ‫معه‬ ‫والمحصور‬ ‫القاعدة‬ ‫فى‬ ‫معه‬ ‫المشترك‬ ‫األضالع‬
‫المشتركة‬ ‫القاعدة‬ ‫هذه‬ ‫يحمل‬ ‫أحدهما‬ ‫متوازيين‬ ‫مستقيمين‬
‫مالحظة‬‫مثلثين‬ ‫إلى‬ ‫سطحه‬ ‫يقسم‬ ‫األضالع‬ ‫متوازى‬ ‫قطر‬ :
‫ا‬ ‫فى‬ ‫متساويين‬ " ‫متطابقين‬" ‫لمساحة‬
: ‫تدريب‬
‫مساحة‬ ‫كانت‬ ‫إذا‬ : ‫السابقة‬ ‫األشكال‬ ‫فى‬‫ا‬= ‫ء‬ ‫حـ‬ ‫ب‬36‫سم‬
۲
‫المشترك‬ ‫المثلث‬ ‫مساحة‬ ‫أوجد‬
‫بين‬ ‫معه‬ ‫والمحصور‬ ‫القاعدة‬ ‫فى‬ ‫معه‬‫المشتر‬ ‫القاعدة‬ ‫هذه‬ ‫يحمل‬ ‫أحدهما‬ ‫متوازيين‬ ‫مستقيمين‬‫ك‬
‫نت‬‫ي‬‫ج‬( ‫ة‬5):‫المثلث‬ ‫سطح‬ ‫مساحة‬=‫!؛‬۲‫قا‬ ‫طول‬‫عدته‬×‫إرتفاعه‬
‫تدريب‬(1):
(1= ‫قاعدته‬ ‫طول‬ ‫الذى‬ ‫المثلث‬ )14= ‫إرتفاعه‬ ، ‫سم‬5‫سم‬
= ‫سطحه‬ ‫مساحة‬ ‫تكون‬0000‫سم‬
۲
(۲= ‫سطحه‬ ‫مساحة‬ ‫الذى‬ ‫المثلث‬ )30‫سم‬
۲
= ‫إرتفاعه‬ ،6‫سم‬
‫قاعدته‬ ‫طول‬ ‫تكون‬=0000‫سم‬
(3= ‫سطحه‬ ‫مساحة‬ ‫الذى‬ ‫المثلث‬ )10‫سم‬
۲
= ‫قاعدته‬ ‫طول‬ ،5‫سم‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫ب‬‫حـ‬‫هـ‬‫ص‬‫ع‬ ‫ر‬
‫ا‬‫ل‬‫ع‬ ‫ب‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬

24. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
= ‫إرتفاعه‬ ‫يكون‬0000‫سم‬
( ‫تدريب‬۲):: ‫اآلتى‬ ‫الجدول‬ ‫إكمل‬
‫المثلث‬ ‫قاعدة‬ ‫طول‬‫المثلث‬ ‫إرتفاع‬‫المثلث‬ ‫سطح‬ ‫مساحة‬
1۲‫سم‬10‫سم‬
0‫سم‬16‫سم‬
8‫سم‬7۲1‫سم‬
۲
5‫م‬۲1‫م‬
۲
۲7‫سم‬60‫سم‬
۲
14‫سم‬70‫سم‬
۲
‫تمــــارين‬
(1): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫مربع‬‫ضلعه‬ ‫طول‬1۲‫سم‬
‫منتصف‬ ‫و‬ ،‫سطح‬ ‫مساحة‬ ‫أوجد‬‫ا‬‫و‬‫حـ‬‫هـ‬
(۲): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬، ‫أضالع‬ ‫متوازى‬M
M،= ‫حـ‬ ‫ب‬16= ‫حـ‬ ‫ء‬ ، ‫سم‬10‫سم‬
= ‫هـ‬ ‫ء‬ ،5‫طول‬ ‫أحسب‬ ‫سم‬
(3): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫أضالع‬ ‫متوازيا‬ ‫هـ‬ ‫حـ‬ ‫ب‬ ‫و‬ ،
: ‫أن‬ ‫أثبت‬
*‫م‬‫الشكل‬ ‫ساحة‬‫ا‬‫ب‬‫و‬ ‫س‬ ‫حـ‬ ‫هـ‬ ‫الشكل‬ ‫مساحة‬ = ‫ء‬ ‫س‬
*‫م‬‫ساحة‬∆‫ا‬‫ب‬= ‫و‬‫م‬‫ساحة‬∆‫هـ‬ ‫حـ‬ ‫ء‬
(4): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫و‬‫مساحته‬ ‫أضالع‬ ‫متوازى‬ ‫هـ‬ ‫حـ‬ ‫ب‬
60‫سم‬
۲
،M،M‫فى‬ ‫يقطعه‬‫ا‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫و‬
‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫هـ‬ ‫ء‬‫حـ‬‫ب‬
‫و‬ ‫ء‬‫ا‬‫حـ‬
‫ب‬‫و‬ ‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬‫هـ‬ ‫و‬
‫س‬
‫ا‬
‫ب‬ ‫حـ‬
‫ء‬ ‫هـ‬‫و‬
‫ء‬ ‫حـ‬‫حـ‬‫ب‬‫ب‬‫ا‬‫و‬ ‫هـ‬

25. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
،‫ا‬= ‫ب‬5( ‫ق‬ ، ‫سم‬‫ال‬= ) ‫هـ‬30ْ: ‫أوجد‬
‫المستطيل‬ ‫مساحة‬‫ا‬‫األضالع‬ ‫متوازى‬ ‫محيط‬ ، ‫ء‬ ‫حـ‬ ‫ب‬‫و‬‫هـ‬ ‫حـ‬ ‫ب‬
(5)‫ف‬: ‫المقابل‬ ‫الشكل‬ ‫ى‬‫سطح‬ ‫مساحة‬ ‫كانت‬ ‫إذا‬∆‫ا‬= ‫هـ‬ ‫ء‬15‫سم‬
۲
‫سطح‬ ‫مساحة‬ ،∆= ‫حـ‬ ‫هـ‬ ‫ب‬۲1‫سم‬
۲
: ‫أحسب‬
: ‫من‬ ‫كل‬ ‫سطح‬ ‫مساحة‬∆‫ا‬‫األضالع‬ ‫متوازى‬ ، ‫هـ‬ ‫ب‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
(6): ‫المتعامدة‬ ‫التربيعية‬ ‫الشبكة‬ ‫على‬
‫المثلث‬ ‫إرسم‬‫ا‬‫حيث‬ ‫حـ‬ ‫ب‬‫ا‬( =5،4، )( = ‫ب‬5،1( = ‫حـ‬ ، )1،۲)
‫سطح‬ ‫مساحة‬ ‫أوجد‬ ‫ثم‬‫المثلث‬‫ا‬‫حـ‬ ‫ب‬
(7): ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫ا‬‫ء‬ ‫حـ‬ ‫ب‬،‫ا‬‫أضالع‬ ‫متوازيا‬ ‫ء‬ ‫و‬ ‫هـ‬
،‫بال‬: ‫أن‬ ‫أثبت‬ } ‫س‬ { =
‫سطح‬ ‫مساحة‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫س‬ ‫ب‬∆‫س‬ ‫و‬ ‫ء‬
(8)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫مربع‬‫المربع‬ ‫محيط‬ ‫كان‬ ‫فإذا‬ ‫منتصف‬ ‫هـ‬ ‫فيه‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬=48‫سم‬
‫سطح‬ ‫مساحة‬ ‫أوجد‬∆‫ا‬‫حـ‬ ‫هـ‬
(0)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫مربع‬، ، ‫أضالعه‬ ‫منتصفات‬ ‫ل‬ ، ‫ع‬ ، ‫ص‬ ، ‫س‬ ‫فيه‬
‫مساح‬ ‫كان‬ ‫فإذا‬ ‫الترتيب‬ ‫على‬ ،‫المربع‬ ‫سطح‬ ‫ة‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬=106‫سم‬
۲
‫أوجد‬
‫ل‬ ‫ع‬ ‫ص‬ ‫س‬ ‫المربع‬ ‫سطح‬ ‫مساحة‬
(10)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫سطحه‬ ‫مساحة‬ ‫أضالع‬ ‫متوازى‬100‫سم‬
۲
، ‫منتصف‬ ‫هـ‬ ،‫يقطع‬
‫فى‬‫م‬‫سطح‬ ‫مساحة‬ ‫أوجد‬∆‫ا‬‫م‬‫ء‬
(11)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫فيه‬ ‫مستطيل‬‫ا‬= ‫ب‬6= ‫حـ‬ ‫ب‬ ، ‫سم‬15‫هـ‬ ، ‫سم‬g‫هـ‬ ،h
‫سطح‬ ‫مساحة‬ ‫أوجد‬∆‫ء‬ ‫حـ‬ ‫هـ‬
(1۲)‫ا‬= ‫حـ‬ ‫ب‬ ‫فيه‬ ‫مثلث‬ ‫حـ‬ ‫ب‬10( ‫ق‬ ، ‫سم‬‫ال‬= ) ‫ب‬30ْ‫رسم‬ ،M‫يقطعه‬
‫سطح‬ ‫مساحة‬ ‫أوجد‬ ‫ء‬ ‫فى‬∆‫ا‬‫رسم‬ ‫إذا‬ ، ‫حـ‬ ‫ب‬M‫طول‬ ‫أوجد‬ ‫هـ‬ ‫فى‬ ‫يقطعه‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬‫و‬
‫س‬
‫ا‬‫هـ‬‫حـ‬ ‫ء‬
‫ب‬‫ا‬
‫ء‬‫ا‬‫ب‬‫ا‬‫ب‬‫حـ‬
‫ء‬ ‫حـ‬
‫ب‬‫حـ‬‫هـ‬ ‫ء‬
‫ا‬‫ب‬
‫ا‬‫ب‬‫ا‬‫ب‬
‫ا‬‫ء‬‫ب‬‫حـ‬
‫هـ‬ ‫حـ‬‫ا‬‫ب‬
‫هـ‬ ‫حـ‬

26. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(13)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫مستطيل‬‫فيه‬‫ا‬= ‫ب‬1۲= ‫حـ‬ ‫ب‬ ، ‫سم‬18، ‫منتصفى‬ ‫ص‬ ، ‫س‬ ، ‫سم‬
‫المنطقة‬ ‫سطح‬ ‫مساحة‬ ‫أوجد‬ ‫الترتيب‬ ‫على‬‫ص‬ ‫ء‬ ‫حـ‬ ‫ب‬ ‫س‬
(14)‫محيطها‬ ‫الشكل‬ ‫مربعة‬ ‫أرض‬ ‫قطعة‬ ‫مساحة‬ ‫أوجد‬64‫متر‬
(15)‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫فيه‬ ‫أضالع‬ ‫متوازى‬‫س‬g: ‫أن‬ ‫أثبت‬
‫سطح‬ ‫مساحة‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫ء‬ ‫س‬∆‫ا‬، ‫ء‬ ‫حـ‬
‫سطح‬ ‫مساحة‬∆‫ا‬‫الشكل‬ ‫سطح‬ ‫مساحة‬ = ‫حـ‬ ‫س‬‫ا‬‫ء‬ ‫س‬ ‫ب‬
: ‫كان‬ ‫إذا‬ ‫و‬ ،‫بال‬{ =‫م‬: ‫أن‬ ‫أثبت‬ }
‫سطح‬ ‫مساحة‬∆‫ا‬‫س‬‫م‬‫سطح‬ ‫مساحة‬ =∆‫حـ‬ ‫ء‬‫م‬
‫تس‬‫مثلثين‬ ‫مساحتى‬ ‫اوى‬
( ‫نظرية‬۲):
‫القاعدة‬ ‫هذه‬ ‫يوازى‬ ‫مستقيم‬ ‫على‬ ‫رأساهما‬ ‫و‬ ‫واحدة‬ ‫قاعدة‬ ‫على‬ ‫المرسومان‬ ‫المثلثان‬
‫يكونان‬‫المساحة‬ ‫فى‬ ‫متساويان‬
‫المعطيات‬:، //∆∆‫ا‬‫حـ‬ ‫ب‬‫مشتركان‬ ‫حـ‬ ‫ب‬ ‫ء‬ ،
‫القاعدة‬
‫المطلوب‬‫مساحة‬ : ‫أن‬ ‫إثبات‬ :∆‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ =∆‫حـ‬ ‫ب‬ ‫ء‬
‫العمــــــل‬:‫نرسم‬M،M
‫البرهان‬:A، //M،M
B‫ا‬‫مستط‬ ‫ء‬ ‫و‬ ‫هـ‬، ‫يل‬‫ا‬‫و‬ ‫ء‬ = ‫هـ‬
،A‫مساحة‬∆‫ا‬‫حـ‬ ‫ب‬=‫!؛‬۲×‫حـ‬ ‫ب‬×‫ا‬( ‫هـ‬1)
،‫مساحة‬∆‫ء‬‫حـ‬ ‫ب‬=‫!؛‬۲×‫حـ‬ ‫ب‬×= ‫و‬ ‫ء‬‫!؛‬۲×‫حـ‬ ‫ب‬×‫ا‬‫هـ‬
(۲)
( ‫من‬1)( ،۲‫مساحة‬ : ‫ينتج‬ )∆‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ =∆‫حـ‬ ‫ب‬ ‫ء‬
‫تدريب‬:// ‫كان‬ ‫إذا‬ ‫المقابل‬ ‫الشكل‬ ‫فى‬‫أكمل‬:
‫ء‬‫ا‬
‫ب‬‫ا‬
‫حـ‬‫ب‬
‫حـ‬‫ا‬‫ء‬ ‫س‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬‫و‬
‫حـ‬‫ب‬
‫ب‬‫حـ‬‫ا‬‫و‬
■ ■
‫ا‬‫هـ‬‫ب‬‫حـ‬‫ب‬‫حـ‬ ‫و‬ ‫ء‬
‫ب‬‫حـ‬‫ا‬‫و‬‫ا‬‫هـ‬‫ب‬‫حـ‬‫ب‬‫حـ‬ ‫و‬ ‫ء‬
‫هـ‬ ‫ء‬‫حـ‬ ‫ب‬‫ا‬

27. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫مساحة‬∆‫ء‬‫حـ‬ ‫ب‬=0000
‫مساحة‬ ‫بإضافة‬∆‫ا‬: ‫ينتج‬ ‫هـ‬ ‫ء‬
‫مساحة‬∆‫ا‬‫ه‬ ‫ب‬‫ـ‬=0000
‫نت‬‫ي‬‫ج‬( ‫ة‬1):
‫الطول‬ ‫فى‬ ‫متساوية‬ ‫قواعدها‬ ‫التى‬ ‫المثلثات‬‫والمحصورة‬
‫بين‬‫تكون‬ ‫متوازيين‬ ‫مستقيمين‬‫المساحة‬ ‫فى‬ ‫متساوية‬
: ‫المقابل‬ ‫الشكل‬ ‫ففى‬‫ل‬ ‫ص‬ = ‫و‬ ‫هـ‬ = ‫حـ‬ ‫ب‬ ، //
‫مساحة‬∆‫ا‬‫ح‬ ‫ب‬‫ـ‬‫مساحة‬ =∆‫ه‬‫ـ‬‫ء‬ ‫و‬
‫مساحة‬ =∆‫ص‬ ‫س‬‫ل‬=‫!؛‬۲×‫حـ‬ ‫ب‬×‫ع‬
‫تدريب‬‫منتصف‬ ‫هـ‬ ، // ‫كان‬ ‫إذا‬ ‫المقابل‬ ‫الشكل‬ ‫فى‬ :
‫أكمل‬:‫مساحة‬∆‫ا‬‫ه‬ ‫ب‬‫ـ‬=0000
‫مساحة‬ ‫بإضافة‬∆: ‫ينتج‬ ‫حـ‬ ‫ب‬ ‫هـ‬
‫مساحة‬∆‫ا‬‫ه‬ ‫ب‬‫ـ‬‫مساحة‬ +∆‫ب‬ ‫هـ‬= ‫حـ‬0000+0000
‫الشكل‬ ‫سطح‬ ‫مساحة‬‫ا‬‫ه‬ ‫حـ‬ ‫ب‬‫ـ‬=0000
‫نت‬‫ي‬‫ج‬( ‫ة‬۲):
‫المساحة‬ ‫فى‬ ‫متساويين‬ ‫مثلثين‬ ‫إلى‬ ‫سطحه‬ ‫يقسم‬ ‫المثلث‬ ‫متوسط‬
‫فى‬ ‫متوسط‬ : ‫المقابل‬ ‫الشكل‬ ‫ففى‬∆‫ا‬‫ح‬ ‫ب‬‫ـ‬
B‫مساحة‬∆‫ا‬‫مساحة‬ = ‫ء‬ ‫ب‬∆‫ا‬= ‫ء‬ ‫حـ‬‫!؛‬۲‫مساحة‬∆‫ا‬‫حـ‬ ‫ب‬
=‫!؛‬۲×‫ء‬ ‫ب‬×‫ا‬‫هـ‬
‫تدريب‬:∆‫ا‬‫مساحة‬ ‫كانت‬ ‫فإذا‬ ‫متوسط‬ ‫فيه‬ ‫حـ‬ ‫ب‬∆‫ا‬= ‫حـ‬ ‫ب‬30‫سم‬
۲
: ‫أكمل‬
A‫فى‬ ‫متوسط‬∆‫ا‬‫حـ‬ ‫ب‬B‫مساحة‬∆‫ا‬= ‫ء‬ ‫ب‬0000=0000
‫نت‬‫ي‬‫ج‬( ‫ة‬3):
‫و‬ ‫الطول‬ ‫فى‬ ‫متساوية‬ ‫قواعدها‬ ‫التى‬ ‫المثلثات‬‫مستقيم‬ ‫على‬
‫الرأس‬ ‫فى‬ ‫مشتركة‬ ‫و‬ ‫واحد‬‫المساحة‬ ‫فى‬ ‫متساوية‬ ‫تكون‬
‫ب‬‫حـ‬
‫ء‬‫هـ‬
‫و‬
■
‫ا‬
‫ب‬‫حـ‬‫ء‬
‫هـ‬‫و‬‫س‬
‫ص‬‫ل‬
‫ع‬
‫ب‬‫حـ‬‫ا‬‫و‬
‫ا‬‫ء‬‫حـ‬ ‫ب‬
‫ب‬‫حـ‬
‫ء‬ ‫هـ‬ ‫ا‬
‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬ ‫ء‬‫هـ‬
■
‫ا‬‫ء‬
‫ا‬‫ء‬
‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬ ‫ء‬‫هـ‬

28. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
: ‫المقابل‬ ‫الشكل‬ ‫ففى‬A‫حـ‬ ‫هـ‬ = ‫هـ‬ ‫ء‬ = ‫ء‬ ‫ب‬
B‫مساحة‬∆‫ا‬‫مساحة‬ = ‫ء‬ ‫ب‬∆‫ا‬‫مساحة‬ = ‫هـ‬ ‫ء‬∆‫ا‬‫حـ‬ ‫هـ‬
‫تدريب‬: ‫السابق‬ ‫الشكل‬ ‫فى‬ :
‫كان‬ ‫إذا‬∆‫ا‬= ‫حـ‬ ‫ب‬45‫سم‬
۲
: ‫أكمل‬
A‫حـ‬ ‫هـ‬ = ‫هـ‬ ‫ء‬ = ‫ء‬ ‫ب‬
B‫مساحة‬∆‫ا‬= ‫ء‬ ‫ب‬0000=0000=0000=0000B‫مساحة‬∆‫ا‬‫حـ‬ ‫ب‬
=0000‫سم‬
۲
( ‫نظرية‬3):
‫واحدة‬ ‫جهة‬ ‫فى‬ ‫و‬ ‫واحدة‬ ‫قاعدة‬ ‫على‬ ‫المرسومان‬ ‫و‬ ‫مساحتيهما‬ ‫فى‬ ‫المتساويان‬ ‫المثلثان‬
‫من‬‫القاعدة‬ ‫هذه‬ ‫يوازى‬ ‫مستقيم‬ ‫على‬ ‫رأساهما‬ ‫يكون‬ ‫القاعدة‬ ‫هذه‬
‫المعطيات‬‫مساحة‬ :∆‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ =∆‫حـ‬ ‫ب‬ ‫ء‬
‫مشتر‬ ‫قاعدة‬ ،‫للمثلثين‬ ‫كة‬
‫المطلوب‬// : ‫أن‬ ‫إثبات‬ :
‫العمــــــل‬:‫نرسم‬M،M
‫البرهان‬:A‫مساحة‬∆‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ =∆‫حـ‬ ‫ب‬ ‫ء‬
B‫!؛‬۲×‫حـ‬ ‫ب‬×‫ا‬= ‫هـ‬‫!؛‬۲×‫حـ‬ ‫ب‬×‫و‬ ‫ء‬
،AM،MB//
B‫الشكل‬‫ا‬: ‫أن‬ ‫وينتج‬ ‫مستطيل‬ ‫ء‬ ‫و‬ ‫هـ‬//
( ‫من‬1( ، )۲‫مساحة‬ : ‫ينتج‬ )∆‫ا‬‫حـ‬ ‫ب‬‫مساحة‬ =∆‫حـ‬ ‫ب‬ ‫ء‬
‫تدريب‬‫كان‬ ‫إذا‬ ‫المقابل‬ ‫الشكل‬ ‫فى‬ :‫مس‬‫احة‬∆‫ا‬‫ب‬‫مساحة‬ = ‫و‬∆‫و‬ ‫حـ‬ ‫ء‬
‫أكمل‬:‫مساحة‬ ‫بإضافة‬∆: ‫ينتج‬ ‫و‬ ‫حـ‬ ‫ب‬
‫مساحة‬∆= ‫ب‬ ‫حـ‬ ‫ء‬0000
‫القاعدة‬ ‫فى‬ ‫مشتركان‬ ‫وهما‬0000‫وفى‬0000
‫ب‬‫حـ‬
‫ء‬
‫و‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬‫و‬
‫حـ‬‫ب‬
‫ب‬‫حـ‬‫ا‬‫و‬■ ■
‫ا‬‫هـ‬‫ب‬‫حـ‬‫ب‬‫حـ‬ ‫و‬ ‫ء‬
‫ب‬‫حـ‬‫ا‬‫و‬
‫ا‬‫هـ‬‫ب‬‫حـ‬ ‫ب‬‫حـ‬‫و‬ ‫ء‬
‫ا‬‫ء‬
‫ا‬
‫ا‬‫هـ‬‫و‬ ‫ء‬

29. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
B//0000
‫تمــــارين‬
(1): ‫المقابل‬ ‫الشكل‬ ‫فى‬//
‫و‬ ،‫سطح‬ ‫مساحة‬∆‫ا‬= ‫و‬ ‫ب‬30‫سم‬
۲
‫أوجد‬‫سطح‬ ‫مساحة‬∆‫و‬ ‫حـ‬ ‫ء‬
(۲): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬، ‫أضالع‬ ‫متوازى‬‫و‬g
‫هـ‬ ،‫منتصف‬،‫سطح‬ ‫مساحة‬∆= ‫و‬ ‫حـ‬ ‫هـ‬15‫سم‬
۲
‫م‬ ‫سطح‬ ‫مساحة‬ ‫أوجد‬‫األضالع‬ ‫توازى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
(3): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫مستطيل‬،‫ا‬‫ص‬ ‫حـ‬ = ‫س‬
= ‫ص‬ ‫س‬ ،‫!؛‬۲‫ا‬‫حـ‬: ‫أن‬ ‫أثبت‬
‫مساحة‬‫سطح‬∆= ‫ص‬ ‫س‬ ‫ب‬‫!؛‬4‫المستطيل‬ ‫سطح‬ ‫مساحة‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
(4): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫فى‬ ‫متوسط‬∆‫ا‬‫حـ‬ ‫ب‬‫منصف‬ ‫هـ‬ ،
: ‫أن‬ ‫أثبت‬‫مساحة‬‫سطح‬∆‫ا‬= ‫هـ‬ ‫ء‬‫!؛‬4‫مساحة‬‫سطح‬∆‫ا‬‫حـ‬ ‫ب‬
‫مساحة‬ ،‫سطح‬∆= ‫ء‬ ‫هـ‬ ‫ب‬‫!؛‬3‫مس‬‫مساحة‬‫سطح‬‫الشكل‬‫ا‬‫حـ‬ ‫ء‬ ‫هـ‬
(5): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫و‬ ، ‫هـ‬g‫حيث‬
‫أن‬ ‫أثبت‬ // ، ‫و‬ ‫حـ‬ = ‫هـ‬ ‫ب‬:
‫الشكل‬ ‫مساحة‬‫ا‬‫الشكل‬ ‫مساحة‬ = ‫ء‬ ‫و‬ ‫ب‬‫ا‬‫ء‬ ‫حـ‬ ‫هـ‬
(6)∆‫ا‬‫متوسطات‬ ‫تالقى‬ ‫نقطة‬ ‫و‬ ، ‫منتصف‬ ‫هـ‬ ، ‫منتصف‬ ‫ء‬ ‫فيه‬ ‫حـ‬ ‫ب‬∆‫ا‬‫حـ‬ ‫ب‬
‫مساحة‬ ‫كانت‬ ‫فإذا‬∆‫ا‬= ‫حـ‬ ‫ب‬60‫سم‬
۲
‫مساحة‬ : ‫أوجد‬∆‫ا‬‫مساحة‬ ، ‫هـ‬ ‫ب‬∆‫حـ‬ ‫و‬ ‫ب‬
‫مساحة‬ ،∆‫ء‬ ‫و‬ ‫ب‬
‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫هـ‬ ‫و‬ ‫ب‬
‫ا‬‫ء‬
‫ا‬‫ء‬
‫ءءحـب‬
‫ب‬‫حـ‬
‫ء‬
‫و‬
‫ا‬ ‫ب‬‫حـ‬
‫و‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫س‬
‫ص‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫ا‬‫ب‬
‫هـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫و‬
‫حـ‬ ‫ب‬
‫ا‬‫ء‬‫حـ‬ ‫ب‬
‫حـ‬ ‫ب‬‫ا‬‫حـ‬
‫ا‬‫و‬

30. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(7)‫ا‬‫ب‬: ‫أن‬ ‫أثبت‬ ‫منتصف‬ ‫هـ‬ ، ‫و‬ ‫فى‬ ‫قطراه‬ ‫تقاطع‬ ‫أضالع‬ ‫متوازى‬ ‫ء‬ ‫حـ‬
‫سطح‬ ‫مساحة‬ **∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫هـ‬ ‫ب‬∆‫ا‬‫هـ‬ ‫ء‬
‫سطح‬ ‫مساحة‬ **∆‫سطح‬ ‫مساحة‬ = ‫حـ‬ ‫هـ‬ ‫ب‬∆‫حـ‬ ‫هـ‬ ‫ء‬
(8): ‫المقابل‬ ‫الشكل‬ ‫فى‬: ‫أن‬ ‫أثبت‬ ‫ص‬ ‫حـ‬ = ‫س‬ ‫ب‬ ، //
‫سطح‬ ‫مساحة‬ *∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫و‬ ‫ب‬∆‫و‬ ‫حـ‬ ‫ء‬
‫الشكل‬ ‫سطح‬ ‫مساحة‬ *‫ا‬‫و‬ ‫ص‬ ‫حـ‬ ‫ء‬ ‫الشكل‬ ‫سطح‬ ‫مساحة‬ = ‫و‬ ‫س‬ ‫ب‬
(0): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫فيه‬ ‫رباعى‬ ‫شكل‬ ‫ء‬ ‫حـ‬ ‫ب‬
، ‫منتصف‬ ‫س‬‫بال‬‫كانت‬ ‫فإذا‬ } ‫و‬ { =
‫ال‬ ‫سطح‬ ‫مساحة‬‫شكل‬‫ا‬‫و‬ ‫ص‬ ‫حـ‬ ‫ء‬ ‫الشكل‬ ‫سطح‬ ‫مساحة‬ = ‫و‬ ‫س‬ ‫ب‬
‫سطح‬ ‫مساحة‬ : ‫أن‬ ‫أثبت‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫و‬ ‫ب‬∆، ‫و‬ ‫حـ‬ ‫ء‬//
(10): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫فيه‬ ‫مستطيل‬ ‫ء‬ ‫حـ‬ ‫ب‬
= ‫حـ‬ ‫ب‬1۲= ‫ء‬ ‫حـ‬ ، ‫سم‬0، ‫سم‬
‫سطح‬ ‫مساحة‬∆‫ا‬= ‫حـ‬ ‫س‬54‫سم‬
۲
‫أ‬// : ‫أن‬ ‫ثبت‬
(11)∆‫ا‬‫ء‬ ، ‫منتصف‬ ‫س‬ ‫فيه‬ ‫حـ‬ ‫ب‬g‫هـ‬ ،g،
‫سطح‬ ‫مساحة‬∆‫سطح‬ ‫مساحة‬ = ‫ء‬ ‫ب‬ ‫س‬∆// ** : ‫أن‬ ‫أثبت‬ ‫هـ‬ ‫حـ‬ ‫س‬
‫سطح‬ ‫مساحة‬ **∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫ب‬ ‫هـ‬∆‫ا‬‫حـ‬ ‫ء‬
‫سط‬ ‫مساحة‬ **‫الشكل‬ ‫ح‬‫ا‬‫الشكل‬ ‫سطح‬ ‫مساحة‬ = ‫هـ‬ ‫س‬ ‫ب‬‫ا‬‫حـ‬ ‫س‬ ‫ء‬
(1۲)∆‫ا‬‫ء‬ ‫فيه‬ ‫حـ‬ ‫ب‬g‫هـ‬ ،g‫بحيث‬‫بال‬، } ‫س‬ { =
‫سطح‬ ‫مساحة‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫ب‬ ‫هـ‬∆‫ا‬// ** : ‫أن‬ ‫أثبت‬ ‫حـ‬ ‫ء‬
‫سطح‬ ‫مساحة‬ **∆‫مسا‬ = ‫س‬ ‫ب‬ ‫ء‬‫سطح‬ ‫حة‬∆‫س‬ ‫حـ‬ ‫هـ‬
(13): ‫المقابل‬ ‫الشكل‬ ‫فى‬، //
‫بال‬، }‫هـ‬ { =
‫ب‬‫حـ‬
‫ء‬
‫و‬
‫ا‬
‫س‬‫ص‬
‫ا‬‫ء‬‫حـ‬ ‫ب‬
‫ب‬‫حـ‬
‫ء‬
‫و‬
‫ا‬
‫س‬
‫حـ‬ ‫ب‬‫ء‬ ‫ب‬‫ا‬‫حـ‬
‫حـ‬ ‫ب‬‫ا‬‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫س‬
‫ء‬ ‫س‬‫ا‬‫حـ‬
‫حـ‬ ‫ب‬‫ا‬‫ب‬‫ا‬‫حـ‬
‫هـ‬ ‫ء‬‫حـ‬ ‫ب‬
‫حـ‬ ‫ب‬
‫ا‬‫ب‬‫ا‬‫حـ‬‫هـ‬ ‫ب‬‫حـ‬ ‫ء‬
‫هـ‬ ‫ء‬
‫ب‬
‫ء‬ ‫ا‬
‫هـ‬
‫ا‬‫ء‬‫حـ‬ ‫ب‬
‫ءءحـب‬ ‫ا‬‫حـ‬‫ء‬ ‫ب‬

31. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫سطح‬ ‫مساحة‬ ‫كانت‬ ‫فإذا‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫ب‬ ‫هـ‬∆‫هـ‬ ‫حـ‬ ‫و‬
‫سطح‬ ‫مساحة‬ : ‫أن‬ ‫اثبت‬∆‫ا‬‫سطح‬ ‫مساحة‬ = ‫ب‬ ‫هـ‬∆‫هـ‬ ‫حـ‬ ‫ء‬
// : ‫أن‬ ‫اثبت‬ ‫ثم‬
‫المعين‬ ‫مساحة‬
‫ن‬‫أن‬ ‫علم‬:
‫الطول‬ ‫فى‬ ‫متساوية‬ ‫أضالعه‬ ‫أضالع‬ ‫متوازى‬ ‫هو‬ ‫المعين‬ **
‫ومتعامدان‬ ‫اآلخر‬ ‫منهما‬ ‫كل‬ ‫ينصف‬ ‫المعين‬ ‫قطرا‬ **
‫زاويتى‬ ‫ينصف‬ ‫منهما‬ ‫كل‬ ‫المعين‬ ‫قطرا‬ **‫بينهما‬ ‫الواصل‬ ‫الرأس‬
: ً‫ال‬‫أو‬‫المعين‬ ‫مساحة‬، ‫ضلعه‬ ‫طول‬ ‫علم‬ ‫إذا‬‫إرتفاعه‬
‫ضلعه‬ ‫طول‬ = ‫المعين‬ ‫مساحة‬×‫إرتفاعه‬
: ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫المعين‬ ‫سطح‬ ‫مساحة‬‫ا‬‫حـ‬ ‫ب‬ = ‫ء‬ ‫حـ‬ ‫ب‬×‫ا‬‫هـ‬
: ‫تدريب‬
‫ضلعه‬ ‫طول‬ ‫معين‬5‫إرت‬ ، ‫سم‬= ‫فاعه‬4‫سم‬
= ‫المعين‬ ‫سطح‬ ‫مساحة‬0000×0000=0000‫سم‬
۲
‫قطريه‬ ‫طوال‬ ‫علم‬ ‫إذا‬ ‫المعين‬ ‫مساحة‬ : ً‫ال‬‫أو‬
= ‫المعين‬ ‫مساحة‬‫!؛‬۲‫قطريه‬ ‫طوال‬ ‫ضرب‬ ‫حاصل‬
: ‫تدريب‬
‫معين‬‫قطريه‬ ‫طوال‬8‫سم‬،6‫سم‬
= ‫المعين‬ ‫سطح‬ ‫مساحة‬0000×0000×0000=0000‫سم‬
۲
‫ن‬‫أن‬ ‫علم‬:
‫حـ‬
‫و‬
‫ء‬ ‫و‬‫هـ‬ ‫حـ‬
‫ب‬
‫حـ‬
‫ء‬
‫و‬
‫ا‬
■ //
=
=
**
**
♦
♦
♦
♦
‫ب‬
‫حـ‬
‫ء‬
‫ا‬
‫هـ‬
‫ب‬‫و‬
‫ا‬
‫حـ‬
‫ء‬ ■

32. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
" ‫قائمة‬ ‫زواياه‬ ‫إحدى‬ ‫أو‬ " ‫الطول‬ ‫فى‬ ‫متساويان‬ ‫قطراه‬ ‫معين‬ ‫هو‬ ‫المربع‬
: ً‫ال‬‫أو‬‫المربع‬ ‫مساحة‬‫ضلعه‬ ‫طول‬ ‫علم‬ ‫إذا‬
‫الضلع‬ ‫طول‬ = ‫المربع‬ ‫مساحة‬×‫نفسه‬
‫قطره‬ ‫طول‬ ‫علم‬ ‫إذا‬ ‫المربع‬ ‫مساحة‬ : ً‫ا‬‫ثاني‬
‫مساحة‬= ‫المربع‬‫!؛‬۲‫قطره‬ ‫طول‬ ‫مربع‬
: ‫تدريب‬
‫المساحة‬ ‫فى‬ ‫أكبر‬ ‫أيهما‬‫قطره‬ ‫طول‬ ‫مربع‬1۲‫ضلعه‬ ‫طول‬ ‫مربع‬ ‫أم‬ ‫سم‬10‫سم‬
= ‫األول‬ ‫المربع‬ ‫مساحة‬
= ‫الثانى‬ ‫المربع‬ ‫مساحة‬
B
‫المنحرف‬ ‫شبه‬
‫هو‬ ‫المنحرف‬ ‫شبه‬:
‫شك‬‫ل‬" ‫قاعدتيه‬ ‫هما‬ " ‫متوازيان‬ ‫ضلعان‬ ‫فيه‬ ‫رباعى‬
" ً‫ا‬‫ساق‬ " ‫المتوازيين‬ ‫غير‬ ‫الضلعين‬ ‫من‬ ‫كل‬ ‫يسمى‬ ‫و‬
‫المنحرف‬ ‫شبه‬ ‫قاعدتا‬ ، : ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
‫المنحرف‬ ‫شبه‬ ‫ساقا‬ ،‫ا‬‫حـ‬ ‫ب‬‫ء‬
‫المنحرف‬ ‫شبه‬ ‫إرتفاع‬ ‫طول‬ ،‫ا‬‫ء‬ ‫حـ‬ ‫ب‬" ‫ع‬ "
‫مالحظات‬:‫واحد‬ ‫إرتفاع‬ ‫له‬ ‫المنحرف‬ ‫شبه‬ **
‫المساحة‬ ‫فى‬ ‫متساويين‬ ‫غير‬ ‫مثلثين‬ ‫إلى‬ ‫يقسمه‬ ‫المنحرف‬ ‫شبه‬ ‫قطر‬ **‫؟‬ ‫لماذا‬
‫المنحرف‬ ‫شبه‬‫الساقين‬ ‫المتساوى‬:
: ‫وفيه‬ " ‫الطول‬ ‫فى‬ ‫تساويا‬ " ‫ساقيه‬ ‫تطابقا‬ ‫منحرف‬ ‫شبه‬ ‫هو‬
‫القياس‬ ‫فى‬ ‫متساويتان‬ ‫قاعدتيه‬ ‫من‬ ‫كل‬ ‫زاويتا‬
‫الطول‬ ‫فى‬ ‫متساويان‬ ‫قطراه‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
■
‫هـ‬
‫ع‬
‫ا‬‫ء‬‫حـ‬ ‫ب‬
‫ا‬‫ب‬‫حـ‬ ‫ء‬
‫ا‬‫ه‬‫ـ‬

33. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫فقط‬ ‫واحد‬ ‫تماثل‬ ‫محور‬ ‫له‬
‫المنحرف‬ ‫شبه‬‫ال‬‫الزاوية‬ ‫قائم‬:
‫المت‬ ‫القاعدتين‬ ‫على‬ ‫عمودى‬ ‫ساقيه‬ ‫أحد‬ ‫فيه‬ ‫منحرف‬ ‫شبه‬ ‫هو‬‫وازيتين‬
: ‫المقابل‬ ‫الشكل‬ ‫فى‬M، ‫من‬ ‫كل‬
‫المنحرف‬ ‫شبه‬ ‫إرتفاع‬ : ‫أن‬ ‫أى‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬‫طول‬ ‫هو‬
‫ل‬ ‫المتوسطة‬ ‫القاعدة‬‫المنحرف‬ ‫شبه‬:
‫المنحرف‬ ‫شبه‬ ‫ساقى‬ ‫منتصفى‬ ‫بين‬ ‫الواصلة‬ ‫المستقيمة‬ ‫القطعة‬ ‫هى‬
: ‫المقابل‬ ‫الشكل‬ ‫فى‬
‫س‬‫الترتيب‬ ‫على‬ ، ‫منتصفى‬ ‫ص‬ ،
‫المنحرف‬ ‫لشبه‬ ‫المتوسطة‬ ‫القاعدة‬ ‫هى‬ ‫فتكون‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬
= ‫طول‬ ، // // : ‫مالحظات‬‫!؛‬۲(‫ا‬) ‫حـ‬ ‫ب‬ + ‫ء‬
‫طوال‬ ‫منحرف‬ ‫شبه‬ : ‫تدريب‬‫المتوازيتين‬ ‫قاعدتيه‬10، ‫سم‬14‫سم‬
= ‫المتوسطة‬ ‫قاعدته‬ ‫طول‬0000
‫مساحة‬‫ل‬‫المنحرف‬ ‫شبه‬:
‫المنحرف‬ ‫شبه‬ ‫مساحة‬‫ا‬‫ء‬ ‫حـ‬ ‫ب‬=
‫مساحة‬∆‫ا‬‫ب‬+ ‫ء‬‫مساحة‬∆‫ب‬‫ء‬ ‫حـ‬=
‫!؛‬۲×‫ا‬‫ء‬×+ ‫و‬ ‫ب‬‫!؛‬۲×‫حـ‬ ‫ب‬×‫هـ‬ ‫ء‬=‫!؛‬۲‫ل‬1×‫ل‬ + ‫ع‬۲×‫ع‬=
‫!؛‬۲‫(ل‬1‫ل‬ +۲× )‫ع‬
= ‫المنحرف‬ ‫شبه‬ ‫مساحة‬‫!؛‬۲‫المتوازيتين‬ ‫قاعدتيه‬ ‫طولى‬ ‫مجموع‬×‫اإلرتفاع‬
‫المتوسطة‬ ‫القاعدة‬ ‫طول‬ =×‫ا‬‫إلرتفاع‬
‫المتوازيتين‬ ‫قاعدتيه‬ ‫طوال‬ ‫منحرف‬ ‫شبه‬ : ‫تدريب‬10، ‫سم‬14‫سم‬‫إرتفاعه‬ ،5‫سم‬
= ‫المنحرف‬ ‫شبه‬ ‫مساحة‬0000
‫من‬ ‫شبه‬ : ‫تدريب‬‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫حرف‬6، ‫سم‬‫مساحته‬60‫سم‬
۲
‫ا‬
‫ب‬ ‫حـ‬
‫ء‬■
■
‫حـ‬ ‫ء‬‫حـ‬ ‫ب‬‫ا‬‫ب‬
‫حـ‬ ‫ء‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫س‬‫ص‬
=
=
--
--
‫حـ‬ ‫ء‬ ‫ا‬‫ب‬
‫ص‬ ‫س‬
‫ص‬ ‫س‬‫حـ‬ ‫ب‬‫ا‬‫ء‬‫ص‬ ‫س‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
‫ع‬‫ع‬
‫هـ‬
‫و‬
‫ل‬1
‫ل‬۲

34. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
= ‫المنحرف‬ ‫شبه‬ ‫مساحة‬0000
: ‫تدريب‬
‫ا‬ ‫الجدول‬ ‫إكمل‬: ‫آلتى‬" ‫المضلعات‬ ‫بعض‬ ‫سطح‬ ‫ومساحة‬ ‫محيط‬ "
‫المضلع‬ ‫إسم‬‫للمضلع‬ ‫الهندسى‬ ‫الشكل‬‫المحيط‬‫السطح‬ ‫مساحة‬
‫المربع‬
‫المستطيل‬
‫األضالع‬ ‫متوازى‬
‫المعين‬
‫المنحرف‬ ‫شبه‬

35. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫المثلث‬
‫تمــــارين‬
(1)‫قطريه‬ ‫طوال‬ ‫معين‬ ‫سطح‬ ‫مساحة‬ ‫أوجد‬15، ‫سم‬1۲‫سم‬
(۲)‫المتوازيتين‬ ‫قاعدتيه‬ ‫طوال‬ ‫منحرف‬ ‫لشبه‬ ‫المتوسطة‬ ‫القاعدة‬ ‫طول‬ ‫أوجد‬7، ‫سم‬15‫سم‬
(3‫محيطه‬ ‫معين‬ ‫سطح‬ ‫مساحة‬ ‫أوجد‬ )40‫إرتفاعه‬ ‫و‬ ، ‫سم‬7‫سم‬
(4‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫منحرف‬ ‫شبه‬ )1۲‫المتوازيتين‬ ‫قاعدتيه‬ ‫إحدى‬ ‫طول‬ ، ‫سم‬0‫سم‬
‫األخرى‬ ‫القاعدة‬ ‫طول‬ ‫أوجد‬
(5‫المتوازيتين‬ ‫قاعدتيه‬ ‫طوال‬ ‫منحرف‬ ‫شبه‬ ‫مساحة‬ ‫أوجد‬ )7، ‫سم‬13‫إرتفاعه‬ ‫و‬ ‫سم‬5‫سم‬
(6‫قطريه‬ ‫طوال‬ ‫معين‬ )16، ‫سم‬1۲‫ضلعه‬ ‫وطول‬ ، ‫سم‬10‫إرتفاعه‬ ‫أوجد‬ ‫سم‬
(7‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫منحرف‬ ‫شبه‬ )0‫سطحه‬ ‫مساحة‬ ، ‫سم‬63‫سم‬
۲
‫إرتفاعه‬ ‫أوجد‬
(8)‫منحر‬ ‫شبه‬‫إرتفاعه‬ ‫ف‬10‫سطحه‬ ‫مساحة‬ ، ‫سم‬150‫سم‬
۲
‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫أوجد‬
(0)‫مساحته‬ ‫مربع‬40‫سم‬
۲
‫محيطه‬ ‫أوجد‬
(10)‫قطره‬ ‫طول‬ ‫مربع‬ ‫مساحة‬ ‫كانت‬ ‫إذا‬10‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫منحرف‬ ‫شبه‬ ‫مساحة‬ ‫تساوى‬ ‫سم‬
10‫سم‬‫المنحرف‬ ‫شبه‬ ‫إرتفاع‬ ‫أوجد‬
(11)‫مربع‬ ‫مساحة‬ ‫كانت‬ ‫إذا‬‫قطره‬ ‫طول‬10‫بعديه‬ ‫أحد‬ ‫مستطيل‬ ‫مساحة‬ ‫تساوى‬ ‫سم‬10‫سم‬
‫المستطيل‬ ‫محيط‬ ‫أوجد‬
(1۲)‫طول‬ ‫يساوى‬ ‫إرتفاعه‬ ‫و‬ ‫الصغرى‬ ‫قاعدته‬ ‫طول‬ ‫ضعف‬ ‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫منحرف‬ ‫شبه‬
‫مساحته‬ ‫كانت‬ ‫فإذا‬ ‫الكبرى‬ ‫قاعدته‬54‫سم‬
۲
‫إرتفاعه‬ ‫و‬ ‫الصغرى‬ ‫قاعدته‬ ‫طول‬ ‫أوجد‬
(13)‫ق‬‫شكل‬ ‫على‬ ‫أرض‬ ‫طعة‬‫مساحته‬ ‫منحرف‬ ‫شبه‬343‫سم‬
۲
‫إرتفاعه‬ ‫و‬7‫طولى‬ ‫بين‬ ‫والنسبة‬ ‫سم‬
‫المتوازيتين‬ ‫قاعدتيه‬3:4‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫أوجد‬

36. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(14)‫محيطه‬ ‫معين‬ ‫مساحة‬ ‫أوجد‬۲8‫زواياه‬ ‫إحدى‬ ‫وقياس‬ ‫سم‬60ْ‫قطريه‬ ‫أحد‬ ‫وطول‬1۲‫سم‬
(15)‫السطح‬ ‫مساحة‬ ‫حيث‬ ‫من‬ ً‫ا‬‫تنازلي‬ ‫رتب‬‫قطره‬ ‫طول‬ ‫مربع‬ :8‫ضلعه‬ ‫طول‬ ‫معين‬ ، ‫سم‬5، ‫سم‬
‫إرتفاعه‬6= ‫إرتفاعه‬ = ‫المتوسطة‬ ‫قاعدته‬ ‫طول‬ ‫منحرف‬ ‫شبه‬ ، ‫سم‬6‫سم‬
‫المساقط‬
‫مستقيم‬ ‫على‬ ‫نقطة‬ ‫مسقط‬:
‫العمود‬ ‫موقع‬ ‫هو‬‫المستقيم‬ ‫على‬ ‫النقطة‬ ‫هذه‬ ‫من‬ ‫المرسوم‬
‫كانت‬ ‫إذا‬ : ‫المقابل‬ ‫الشكل‬ ‫فى‬:‫ا‬h‫ب‬ ، ‫ل‬g‫ل‬
‫رسم‬ ،M‫حيث‬ ‫ل‬‫ا‬
/
g‫ل‬‫فإن‬‫النقطة‬ :‫ا‬
/
‫النقطة‬ ‫من‬ ‫المرسوم‬ ‫العمود‬ ‫موقع‬ " ‫وهى‬
‫ا‬‫للنقطة‬ ‫العمودى‬ ‫بالمسقط‬ ‫تسمى‬ " ‫ل‬ ‫المستقيم‬ ‫على‬‫ا‬‫ل‬ ‫المستقيم‬ ‫على‬
‫ب‬ ‫النقطة‬ ‫مسقط‬ ‫أما‬ ،g‫ب‬ ‫النقطة‬ ‫نفس‬ ‫فهو‬ ‫ل‬
‫مسق‬‫ط‬‫مستقيمة‬ ‫قطعة‬‫مستقيم‬ ‫على‬:
‫على‬ ‫مسقط‬ ‫إليجاد‬: ‫نرسم‬ ‫ل‬ ‫المستقيم‬
‫ا‬
/
‫مسقط‬‫ا‬، ‫ل‬ ‫المستقيم‬ ‫على‬‫ب‬
/
‫ل‬ ‫المستقيم‬ ‫على‬ ‫ب‬ ‫مسقط‬
‫ل‬ ‫المستقيم‬ ‫على‬ ‫مسقط‬ ‫هى‬ : ‫فتكون‬
‫حـ‬ ‫كانت‬ ‫إذا‬ ،g‫ا‬ ‫على‬ ‫مسقطها‬ ‫فإن‬‫حـ‬ ‫هو‬ ‫ل‬ ‫لمستقيم‬
/
g
: ‫مالحظة‬
‫مسقط‬ ‫طول‬‫نفسها‬ ‫المستقيمة‬ ‫القطعة‬ ‫من‬ ‫أصغر‬ ‫أو‬ ً‫ا‬‫مساوي‬ ‫يكون‬ ‫مستقيم‬ ‫على‬ ‫مستقيمة‬ ‫قطعة‬ ‫أى‬
: ‫تدريب‬: ‫تستنج‬ ‫ماذا‬ ‫وأذكر‬ ‫شكل‬ ‫كل‬ ‫فى‬ ‫المستقيمة‬ ‫القطع‬ ‫مسقط‬ ‫أوجد‬
‫المستقيم‬ ‫على‬ ‫مسقط‬‫مسقط‬‫المستقيم‬ ‫على‬
‫هو‬ ‫ل‬0000‫هو‬ ‫ل‬0000
‫مسقط‬ ‫طول‬0000‫مسقط‬ ‫طول‬0000
‫المستقيم‬ ‫على‬ ‫مسقط‬‫ع‬ ‫مسقط‬‫المستقيم‬ ‫لى‬
‫هو‬ ‫ل‬0000‫هو‬ ‫ل‬0000
‫ل‬
‫ا‬
‫ب‬ ‫ا‬
/
■
‫ا‬‫ا‬
/
‫ل‬
‫ا‬
‫ا‬
/
■■
‫ب‬
‫ب‬
/
‫ا‬‫ب‬
‫ا‬
/
‫ب‬
/
‫ا‬
‫ب‬
‫ا‬
‫ب‬
‫ا‬
/
‫ب‬
/
■
‫حـ‬
‫حـ‬
/
‫ل‬
‫ا‬
‫ب‬
‫ل‬
‫ا‬
‫ب‬
‫ا‬
‫ب‬
‫ا‬
‫ب‬ ‫ا‬
‫ب‬
‫ا‬
‫ب‬
‫ل‬
‫ا‬‫ب‬
‫ا‬
‫ب‬
‫ا‬
‫ب‬
‫ا‬
‫ب‬

37. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫مسقط‬ ‫طول‬0000
‫مسقط‬ ‫طول‬0000‫المستقيمة‬ ‫القطعة‬ ‫من‬ ‫المكون‬ ‫الشكل‬ ‫إسم‬ ‫ما‬
‫؟‬ ‫ل‬ ‫المستقيم‬ ‫على‬ ‫ومسقطها‬
‫المقابل‬ ‫الشكل‬ ‫فى‬ : ‫تدريب‬∆‫ا‬‫ب‬‫فيه‬ ‫حـ‬M
M،M: ‫يأتى‬ ‫ما‬ ‫أكمل‬
(1‫مسقط‬ )‫هو‬ ‫على‬0000
(۲‫مسقط‬ )‫هو‬ ‫على‬0000
(3)‫م‬‫سقط‬‫هو‬ ‫على‬0000
(4‫مسقط‬ )‫هو‬ ‫على‬0000(5‫مسقط‬ )‫على‬‫هو‬0000
(6‫مسقط‬ )‫هو‬ ‫على‬0000(7‫مسقط‬ )‫على‬‫هو‬0000
(8‫مسقط‬ )‫هو‬ ‫على‬0000(0‫مسقط‬ )‫على‬‫هو‬0000
(10‫هو‬ ‫على‬ ‫مسقط‬ )0000(11‫مسقط‬ )‫على‬‫هو‬0000
‫مسقط‬‫شعاع‬‫مستقيم‬ ‫على‬:
: ‫تدريب‬
‫مستقيم‬ ‫على‬ ‫شعاع‬ ‫مسقط‬ ‫توضح‬ ‫مختلفة‬ ‫أشكال‬ ‫أرسم‬
‫مسقط‬‫مستقيم‬‫مستقيم‬ ‫على‬‫آخر‬:
: ‫تدريب‬
‫آخر‬ ‫مستقيم‬ ‫على‬ ‫مستقيم‬ ‫مسقط‬ ‫توضح‬ ‫مختلفة‬ ‫أشكال‬ ‫أرسم‬
‫ل‬
‫ا‬
‫ب‬
‫ا‬
‫هـ‬
‫ح‬ ‫ب‬‫ـ‬
‫ب‬‫و‬‫ا‬‫حـ‬
‫ء‬ ‫حـ‬‫ا‬‫ب‬
‫ا‬
‫ب‬‫حـ‬
‫هـ‬
‫و‬ ‫ء‬
‫م‬ ‫ا‬‫ب‬‫ا‬‫حـ‬
‫ب‬
‫حـ‬
‫ا‬‫ب‬
‫ا‬‫حـ‬‫ب‬
‫حـ‬ ‫ا‬‫حـ‬‫ا‬‫ب‬
‫ا‬‫هـ‬‫ب‬‫حـ‬
‫م‬‫حـ‬‫ا‬‫حـ‬
‫ا‬‫ب‬‫ب‬‫حـ‬
‫م‬‫ب‬‫ب‬‫حـ‬
‫ا‬‫ب‬‫ا‬‫ه‬‫ـ‬
‫م‬‫ء‬‫ا‬‫ب‬‫ا‬‫حـ‬‫ء‬‫حـ‬

38. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫فيثاغورس‬ ‫نظرية‬ ‫عكس‬
‫أن‬ ‫نعلم‬:‫ن‬ "" ‫فيثاغورس‬ ‫ظرية‬‫المربع‬ ‫سطح‬ ‫مساحة‬ ‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫فى‬
‫على‬ ‫المنشأين‬ ‫المربعين‬ ‫مساحتى‬ ‫مجموع‬ ‫يساوى‬ ‫الوتر‬ ‫على‬ ‫المنشأ‬
‫اآلخرين‬ ‫الضلعين‬
: ‫المقابل‬ ‫الشكل‬ ‫فى‬∆‫ا‬‫ب‬‫ب‬ ‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬
(‫ا‬‫حـ‬)
۲
( =‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
: ‫منها‬ ،(‫ا‬‫ب‬)
۲
( =‫ا‬‫حـ‬)
۲
–(‫حـ‬ ‫ب‬)
۲
،(‫ب‬‫حـ‬)
۲
( =‫ا‬‫حـ‬)
۲
–(‫ا‬‫ب‬
)
۲
‫فيثاغورس‬ ‫نظرية‬ ‫عكس‬:
‫المربع‬ ‫مساحة‬ ‫يساوى‬ ‫مثلث‬ ‫أضالع‬ ‫من‬ ‫ضلعين‬ ‫على‬ ‫المنشأين‬ ‫المربعين‬ ‫مساحتى‬ ‫مجموع‬ ‫كان‬ ‫إذا‬
‫المن‬‫قائمة‬ ‫الضلع‬ ‫لهذا‬ ‫المقابلة‬ ‫الزاوية‬ ‫كانت‬ ‫الثالث‬ ‫الضلع‬ ‫على‬ ‫شأ‬
‫فى‬ : ‫أن‬ ‫أى‬∆‫ا‬‫ب‬: ‫كان‬ ‫إذا‬ ‫حـ‬(‫ا‬‫حـ‬)
۲
( =‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
‫فإن‬:‫ق‬(‫ال‬‫ب‬)=00ْْ
‫فى‬ : ‫نتيجة‬∆‫ا‬‫ب‬‫أكبر‬ : ‫كان‬ ‫إذا‬ ‫حـ‬ً‫ال‬‫طو‬ ‫األضالع‬
‫كان‬ ‫و‬(‫ا‬‫حـ‬)
۲
≠(‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
: ‫فإن‬∆‫ا‬‫ب‬‫الزاوية‬ ‫قائم‬ ‫يكون‬ ‫ال‬ ‫حـ‬
‫حيث‬ ‫اآلتى‬ ‫الجدول‬ ‫أكمل‬ : ‫تدريب‬∆‫ا‬‫ب‬‫ب‬ ‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬
‫ا‬‫ب‬360155107011
‫ب‬‫حـ‬48151۲840
‫ا‬‫حـ‬515۲7۲5۲617۲561
‫هل‬ ‫بين‬ : ‫تدريب‬∆‫ا‬‫ب‬: ‫اآلتى‬ ‫الجدول‬ ‫فى‬ ‫ال‬ ‫أم‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬
‫ا‬‫ب‬6014151014735011
‫ب‬ ‫حـ‬■
‫ا‬‫حـ‬
‫ا‬

39. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫ب‬‫حـ‬81015۲7۲48۲741۲4060
‫ا‬‫حـ‬1015۲7۲5۲617۲55134461
∆‫ا‬‫ب‬‫حـ‬
‫المقابل‬ ‫الشكل‬ ‫فى‬ : ‫تدريب‬
‫ا‬‫ب‬‫ء‬ ‫حـ‬‫فيه‬ ‫رباعى‬ ‫شكل‬‫ق‬(‫ال‬‫ب‬)=00ْْ
،‫ا‬‫ب‬=15= ‫حـ‬ ‫ب‬ ، ‫سم‬۲7= ‫ء‬ ‫جـ‬ ، ‫سم‬7‫سم‬
،‫ا‬= ‫ء‬۲4‫سم‬‫أن‬ ‫أثبت‬ ‫ثم‬ ‫طول‬ ‫أوجد‬‫ق‬(‫ال‬‫ء‬)=00ْْ
‫الشكل‬ ‫مساحة‬ ‫أوجد‬ ،‫ا‬‫ب‬‫ء‬ ‫حـ‬
‫الحلــــــــــــــــــ‬
‫فى‬∆‫ا‬‫ب‬‫حـ‬A‫ق‬(‫ال‬‫ب‬)=00ْْB(‫ا‬‫حـ‬)
۲
=0000
B‫ا‬‫حـ‬=0000
‫فى‬∆‫ا‬‫ب‬‫حـ‬A(‫ا‬‫حـ‬)
۲
=0000،(‫ا‬‫ء‬)
۲
=0000،(‫حـ‬‫ء‬)
۲
=0000
B(‫ا‬‫حـ‬)
۲
=0000B0000
‫الشكل‬ ‫مساحة‬‫ا‬‫ب‬‫مساحة‬ = ‫ء‬ ‫حـ‬∆‫ا‬‫ب‬+ ‫حـ‬0000=0000+0000
=0000
‫إقليدس‬ ‫نظرية‬
‫المستطيل‬ ‫مساحة‬ ‫يساوى‬ ‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫فى‬ ‫القائمة‬ ‫ضلعى‬ ‫أحد‬ ‫على‬ ‫المنشأ‬ ‫المربع‬ ‫مساحة‬
‫الوتر‬ ‫وطول‬ ‫الوتر‬ ‫على‬ ‫الضلع‬ ‫هذا‬ ‫مسقط‬ ‫طول‬ ‫بعداه‬ ‫الذى‬
‫ف‬‫ف‬: ‫المقابل‬ ‫الشكل‬ ‫ى‬
∆‫ا‬‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬ ‫ب‬‫ا‬،‫ا‬‫ء‬M‫حـ‬ ‫ب‬
‫فإن‬:B(‫ا‬) ‫ب‬
۲
‫ب‬ ‫ء‬ =×‫حـ‬ ‫ب‬
( ،‫ا‬) ‫حـ‬
۲
‫حـ‬ ‫ء‬ =×‫حـ‬ ‫ب‬
‫ا‬‫حـ‬
‫ا‬
‫ب‬‫حـ‬
‫ء‬
■
‫ء‬
‫ا‬
‫ء‬
‫ب‬‫ح‬
‫ـ‬
■

40. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
( ،‫ا‬) ‫ء‬
۲
‫حـ‬ ‫ء‬ =×‫ب‬ ‫ء‬
‫ء‬ ،‫ا‬×= ‫حـ‬ ‫ب‬‫ا‬‫ب‬×‫ا‬‫حـ‬‫؟‬ ‫لماذا‬
‫تدريب‬:
‫ف‬: ‫المقابل‬ ‫الشكل‬ ‫ى‬: ‫كان‬ ‫إذا‬
∆‫ا‬‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫حـ‬ ‫ب‬‫ا‬،‫ا‬‫ء‬M‫حـ‬ ‫ب‬
= ‫ء‬ ‫ب‬ ،0= ‫حـ‬ ‫ء‬ ، ‫سم‬16: ‫فإن‬ ‫سم‬
(‫ا‬) ‫ب‬
۲
=0000×0000=0000B‫ا‬‫ب‬=0000
،(‫ا‬) ‫حـ‬
۲
=0000×0000=0000B‫ا‬‫حـ‬=0000
،(‫ا‬) ‫ء‬
۲
=0000×0000=0000B‫ا‬‫ء‬=0000
‫زواياه‬ ‫لقياسات‬ ‫بالنسبة‬ ‫المثلث‬ ‫نوع‬ ‫على‬ ‫التعرف‬
‫أن‬ ‫نعلم‬‫ف‬ :ً‫ال‬‫طو‬ ‫المثلث‬ ‫فى‬ ‫ضلعين‬ ‫أصغر‬ ‫تقابالن‬ ‫وهما‬ ‫األقل‬ ‫على‬ ‫حادتان‬ ‫زاويتان‬ ‫توجد‬ ‫مثلث‬ ‫أى‬ ‫ى‬
‫أطوال‬ ‫علمت‬ ‫إذا‬ " ‫زواياه‬ ‫لقياسات‬ ‫بالنسبة‬ ‫المثلث‬ ‫نوع‬ " ‫المثلث‬ ‫فى‬ ‫زاوية‬ ‫أكبر‬ ‫نوع‬ ‫لتحديد‬ **
‫الضلعين‬ ‫طولى‬ ‫مربعى‬ ‫ومجموع‬ ‫فيه‬ ‫األكبر‬ ‫الضلع‬ ‫طول‬ ‫مربع‬ ‫بين‬ ‫نقارن‬ ‫الثالثة‬ ‫أضالعه‬‫اآلخرين‬
(1): ‫كان‬ ‫إذا‬(‫ا‬‫حـ‬)
۲
( =‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
‫اآلخرين‬ ‫الضلعين‬ ‫طولى‬ ‫مربعى‬ ‫مجموع‬ = ‫األكبر‬ ‫الضلع‬ ‫طول‬ ‫مربع‬
‫كانت‬‫ال‬‫ب‬" ‫ب‬ ‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫المثلث‬ " ‫قائمة‬
(۲): ‫كان‬ ‫إذا‬(‫ا‬‫حـ‬)
۲
>(‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
‫اآلخرين‬ ‫الضلعين‬ ‫طولى‬ ‫مربعى‬ ‫مجموع‬ > ‫األكبر‬ ‫الضلع‬ ‫طول‬ ‫مربع‬
‫كانت‬‫ال‬‫ب‬" ‫ب‬ ‫فى‬ ‫الزاوية‬ ‫منفرج‬ ‫المثلث‬ " ‫منفرجة‬
(3): ‫كان‬ ‫إذا‬(‫ا‬‫حـ‬)
۲
<(‫ا‬‫ب‬)
۲
( +‫حـ‬ ‫ب‬)
۲
‫ا‬ ‫طول‬ ‫مربع‬‫اآلخرين‬ ‫الضلعين‬ ‫طولى‬ ‫مربعى‬ ‫مجموع‬ < ‫األكبر‬ ‫لضلع‬
‫كانت‬‫ال‬‫ب‬" ‫الزوايا‬ ‫حاد‬ ‫المثلث‬ " ‫حادة‬
‫ء‬
‫ا‬
‫ء‬
‫ب‬‫ح‬
‫ـ‬
■

41. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
‫نوع‬ ‫بين‬ : ‫تدريب‬∆‫ا‬‫ب‬: ‫اآلتى‬ ‫الجدول‬ ‫فى‬ ‫زواياه‬ ‫لقياسات‬ ‫بالنسبة‬ ‫حـ‬
‫ا‬‫ب‬651۲1۲1037711507
‫ب‬‫حـ‬8315۲78۲5۲7۲71۲1016
‫ا‬‫حـ‬1070۲5743۲513131314
∆‫ا‬‫ب‬‫حـ‬
‫تمــــارين‬
(1): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ا‬‫ب‬‫فيه‬ ‫رباعى‬ ‫شكل‬ ‫ء‬ ‫حـ‬
‫ق‬(‫ال‬‫ب‬)=‫ق‬(‫ال‬‫ء‬)=00ْ،‫ا‬‫ب‬=7‫سم‬
،‫ا‬= ‫ء‬15= ‫ء‬ ‫حـ‬ ، ‫سم‬۲7‫سم‬‫أ‬: ‫من‬ ‫كل‬ ‫طول‬ ‫وجد‬
،
(۲): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ل‬ ‫ع‬ ‫ص‬ ‫س‬‫فيه‬ ‫رباعى‬ ‫شكل‬
‫ق‬(‫ال‬‫ص‬)=‫ق‬(‫ال‬‫ل‬ ‫ع‬ ‫س‬)=00ْ= ‫ص‬ ‫س‬ ،0‫سم‬
= ‫ع‬ ‫ص‬ ،1۲= ‫ل‬ ‫س‬ ، ‫سم‬۲5‫طول‬ ‫أوجد‬ ‫سم‬
‫ص‬ ‫س‬ ‫الشكل‬ ‫مساحة‬ ،‫ل‬ ‫ع‬
(3)‫ا‬‫ب‬‫فيه‬ ‫مستطيل‬ ‫ء‬ ‫حـ‬‫ا‬‫ب‬=8، ‫سم‬‫ا‬= ‫حـ‬17‫مساحته‬ ‫أوجد‬ ‫سم‬
(4)‫ا‬‫ب‬‫قطريه‬ ‫طوال‬ ‫معين‬ ‫ء‬ ‫حـ‬18، ‫سم‬۲4‫محيطه‬ ‫أحسب‬ , ‫ضلعه‬ ‫طول‬ ‫أوجد‬ ‫سم‬
(5)‫ل‬ ‫ع‬ ‫ص‬ ‫س‬‫فيه‬ ‫رباعى‬ ‫شكل‬‫ق‬(‫ال‬‫ص‬)=00ْ= ‫ص‬ ‫س‬ ،3= ‫ع‬ ‫ص‬ ، ‫سم‬4
‫سم‬
= ‫ل‬ ‫ع‬ ،1۲= ‫ل‬ ‫س‬ ، ‫سم‬13: ‫أن‬ ‫أثبت‬ ‫سم‬‫ق‬(‫ال‬‫ل‬ ‫ع‬ ‫س‬)=00ْْ
(6)‫ا‬‫ب‬‫فيه‬ ‫مثلث‬ ‫حـ‬‫ا‬‫ب‬=‫ا‬= ‫حـ‬10= ‫حـ‬ ‫ب‬ ، ‫سم‬1۲‫سم‬‫مساحته‬ ‫أوجد‬
‫ا‬
‫ب‬ ‫حـ‬
‫ء‬
■
‫ا‬‫حـ‬‫ب‬‫حـ‬
‫س‬
‫ص‬ ‫ع‬
‫ل‬
‫ل‬ ‫ع‬

42. ‫الشنتوري‬ ‫أحمد‬a_shantory2007@yahoo.com
‫الصف‬‫الثانى‬ ‫الدراسى‬ ‫الفصل‬ ‫الهندسة‬ ‫اإلعدادى‬ ‫الثانى‬
(7‫رسم‬ ، ‫ص‬ ‫فى‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ‫ع‬ ‫ص‬ ‫س‬ )M‫س‬ ‫كان‬ ‫فإذا‬= ‫ص‬6‫سم‬
= ‫ع‬ ‫ص‬ ،8‫طول‬ ‫أوجد‬ ‫ثم‬ ‫على‬ ‫مسقط‬ ‫طول‬ ‫أوجد‬ ‫سم‬
(8): ‫المقابل‬ ‫الشكل‬ ‫فى‬‫ل‬ ‫ع‬ ‫ص‬ ‫س‬‫فيه‬ ‫رباعى‬ ‫شكل‬
‫ق‬(‫ال‬‫ع‬ ‫ص‬ ‫س‬)=‫ق‬(‫ال‬‫ل‬ ‫ع‬ ‫س‬)=00ْ،
M‫ع‬ ‫ص‬ ،=0، ‫سم‬= ‫ل‬ ‫ع‬8، ‫سم‬
= ‫ل‬ ‫س‬17، : ‫من‬ ‫كل‬ ‫طول‬ ‫أوجد‬ ‫سم‬
‫على‬ ‫مسقط‬ ،
(0)‫ا‬‫ب‬، ‫فيه‬ ‫أضالع‬ ‫متوازى‬ ‫ء‬ ‫حـ‬‫ا‬‫ب‬=15، ‫سم‬‫ا‬= ‫ء‬۲5، ‫سم‬M
‫رسم‬M‫األضالع‬ ‫متوازى‬ ‫مساحة‬ ‫أوجد‬‫ا‬‫ب‬، ‫من‬ ‫كل‬ ‫طول‬ ، ‫ء‬ ‫حـ‬
(10)‫ا‬‫ب‬‫مساحته‬ ‫مستطيل‬ ‫ء‬ ‫حـ‬48‫سم‬
۲
،‫ا‬‫ب‬=6‫رسم‬ ، ‫سم‬M
‫على‬ ‫مسقط‬ ، : ‫من‬ ‫كل‬ ‫طول‬ ‫أوجد‬
(11)∆‫ا‬‫ب‬‫فيه‬ ‫حـ‬‫ا‬‫ب‬=18= ‫حـ‬ ‫ب‬ ، ‫سم‬۲4= ‫ء‬ ‫ب‬ ، ‫منتصف‬ ‫ء‬ ، ‫سم‬15‫سم‬
‫رسم‬ ،: ‫أن‬ ‫أثبت‬ ‫هـ‬ ‫فى‬ ‫ويقطع‬ //‫ق‬(‫ال‬‫ا‬‫ب‬‫حـ‬)=00ْْ
‫طول‬ ‫أوجد‬ ‫ثم‬
(1۲)‫ا‬‫ب‬= ‫حـ‬ ‫ب‬ ‫فيه‬ ‫مستطيل‬ ‫ء‬ ‫حـ‬۲‫ا‬‫ب‬‫هـ‬ ،g‫ا‬: ‫أن‬ ‫ثبت‬
) ‫ب‬ ‫هـ‬ (
۲
) ‫هـ‬ ‫حـ‬ ( +
۲
‫هـ‬ ( =‫ا‬)
۲
) ‫ء‬ ‫هـ‬ ( +
۲
+‫!؛‬۲(‫ا‬) ‫ء‬
۲
(13)‫نوع‬ ‫حدد‬∆‫ا‬‫ب‬: ‫زواياه‬ ‫لقياسات‬ ‫بالنسبة‬ ‫يأتى‬ ‫ما‬ ‫فى‬ ‫حـ‬
1)∆‫ا‬‫ب‬=5‫سم‬= ‫حـ‬ ‫ب‬ ،۲5‫سم‬،‫ا‬= ‫حـ‬۲7‫سم‬
۲)∆‫ا‬‫ب‬=۲5= ‫حـ‬ ‫ب‬ ، ‫سم‬10‫سم‬،‫ا‬= ‫حـ‬۲4‫سم‬
3)∆‫ا‬‫ب‬=37‫سم‬= ‫حـ‬ ‫ب‬ ،35، ‫سم‬‫ا‬= ‫حـ‬1۲‫سم‬
4)∆‫ا‬‫ب‬=۲‫ن‬ ‫م‬‫سم‬= ‫حـ‬ ‫ب‬ ،‫م‬
۲
+‫ن‬
۲
‫سم‬،‫ا‬‫ح‬= ‫ـ‬‫م‬
۲
–‫ن‬
۲
‫سم‬
5)∆‫ا‬‫ب‬=7‫سم‬= ‫حـ‬ ‫ب‬ ،1۲‫سم‬،‫ا‬= ‫حـ‬15‫سم‬
‫ل‬ ‫ص‬‫س‬ ‫ع‬
‫ص‬ ‫س‬‫ع‬ ‫س‬‫ل‬ ‫ص‬
‫س‬
‫ص‬ ‫ع‬
‫ل‬‫و‬
‫و‬ ‫ص‬‫ع‬ ‫س‬
‫ع‬ ‫س‬‫و‬ ‫ص‬
‫س‬ ‫ص‬‫ع‬ ‫س‬
‫ب‬ ‫ء‬‫ا‬‫ب‬
‫هـ‬ ‫ء‬‫ب‬
‫حـ‬
‫هـ‬ ‫ء‬‫هـ‬ ‫حـ‬
‫هـ‬ ‫ب‬‫ا‬‫حـ‬
‫ا‬‫حـ‬‫ا‬‫حـ‬ ‫ا‬‫ب‬
‫ا‬‫حـ‬
‫هـ‬ ‫ء‬‫حـ‬
‫ب‬
‫ا‬‫ب‬
‫ا‬‫حـ‬
‫ا‬‫ء‬