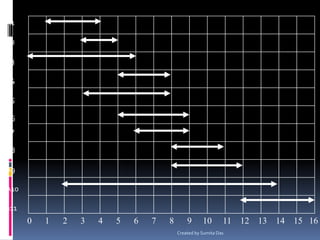
The document describes an activity selection problem where a set of activities must share a single resource. Each activity has a start and finish time, and activities are mutually compatible if one activity finishes before another starts. The problem is to find the maximum subset of mutually compatible activities. A recursive greedy algorithm is presented that takes the activities sorted by finish time and recursively selects the next compatible activity to build the subset. Pseudocode for the algorithm is provided and stepped through on a sample activity set to produce the optimal subset.

1. AN ACTIVITY-SELECTION PROBLEM
BY SUMITA DAS
Created by Sumita Das

2. An Activity-selection problem
 Suppose we have a set of activities S={a1,a2,….,an} (Total n
activities) that wish to use a common resource which can serve
only one activity at a time.
 Mutually exclusive access to single resource.
 Each activity ai is having start time si and finish time fi, where
0<=si<=fi<∞
 Goal: To find a maximum-size subset of mutually compatible
activities
 Compatible Activities: Activities ai and aj are compatible if si>=fj
or sj>=fi
i.e. Second Activity starts before first activity finishes.
Created by Sumita Das

3. Let set S consists of following activities which is sorted in
monotonically increasing order of finish time.
k 0 1 2 3 4 5 6 7 8 9 10 11
sk - 1 3 0 5 3 5 6 8 8 2 12
fk 0 4 5 6 7 8 9 10 11 12 14 16
Created by Sumita Das

4. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
a11
Created by Sumita Das

5. RECURSIVE-ACTIVITY-SELECTOR( s, f, k, n)
1. m= k +1
2. while m <= n and s[m] < f[k]
3. m=m +1
4. if m <= n
5. then return {am}U RECURSIVE-ACTIVITY- SELECTOR
(s, f, m, n)
6. else return Ø
A Recursive Greedy Algorithm
Created by Sumita Das

6. s- array of start time of activities
f- array of finish time of activities
k- index of subproblem Sk
Where Sk is the set of activities that start after activity ak
finishes.
n- size of original problem
 Add a fictitious activity a0 with f0=0
 So Subproblem S0 is entire set of activities S.
 Initial call RECURSIVE-ACTIVITY-SELECTOR( s, f, 0,
n) solves the entire problem
Created by Sumita Das

7. RECURSIVE-ACTIVITY-SELECTOR( s, f, 0, 11)
1. m= k +1
2. while m <= n and s[m] < f[k]
3. m=m +1
4. if m <= n
5. then return {am}U RECURSIVE-ACTIVITY- SELECTOR
(s, f, m, n)
6. else return Ø
k=0 m=0+1=1
1<=11 and s[1]<f[0]
1<=11
1<0 false. While loop exits
Return a1 U RECURSIVE-
ACTIVITY- SELECTOR (s, f,
1, 11)
k 0 1 2 3 4 5 6 7 8 9 10 11
sk - 1 3 0 5 3 5 6 8 8 2 12
fk 0 4 5 6 7 8 9 10 11 12 14 16
Created by Sumita Das

8. RECURSIVE-ACTIVITY-SELECTOR( s, f, 1, 11)
1. m= k +1
2. while m <= n and s[m] < f[k]
3. m=m +1
4. if m <= n
5. then return {am}U RECURSIVE-ACTIVITY- SELECTOR
(s, f, m, n)
6. else return Ø
k=1 m=1+1=2
2<=11 and s[2]<f[1] 3<4 true
m=2+1=3
3<=11 and s[3]<f[1] 0<4 true
m=3+1=4
4<=11 and s[4]<f[1] 5<4 false. While loop exits4<=11
Return a4 U RECURSIVE-
ACTIVITY- SELECTOR (s, f,
4, 11)
k 0 1 2 3 4 5 6 7 8 9 10 11
sk - 1 3 0 5 3 5 6 8 8 2 12
fk 0 4 5 6 7 8 9 10 11 12 14 16
Created by Sumita Das

9. RECURSIVE-ACTIVITY-SELECTOR( s, f, 4, 11)
1. m= k +1
2. while m <= n and s[m] < f[k]
3. m=m +1
4. if m <= n
5. then return {am}U RECURSIVE-ACTIVITY- SELECTOR
(s, f, m, n)
6. else return Ø
k=4 m=4+1=5
5<=11 and s[5]<f[4] 3<7 true
m=5+1=6
6<=11 and s[6]<f[4] 5<7 true
m=6+1=7
7<=11 and s[7]<f[4] 6<7 true
m=7+1=8
8<=11 and
s[8]<f[4] 8<7 false.While loop exits8<=11
Return a8 U RECURSIVE-
ACTIVITY- SELECTOR (s, f,
8, 11)
k 0 1 2 3 4 5 6 7 8 9 10 11
sk - 1 3 0 5 3 5 6 8 8 2 12
fk 0 4 5 6 7 8 9 10 11 12 14 16
Created by Sumita Das

10. RECURSIVE-ACTIVITY-SELECTOR( s, f, 8, 11)
1. m= k +1
2. while m <= n and s[m] < f[k]
3. m=m +1
4. if m <= n
5. then return {am}U RECURSIVE-ACTIVITY- SELECTOR
(s, f, m, n)
6. else return Ø
k=8 m=8+1=9
9<=11 and s[9]<f[8] 8<11 true
m=9+1=10
10<=11 and s[10]<f[8] 2<11 true
m=10+1=11
11<=11 and s[11]<f[8] 12<11 falseWhile
loop exits
11<=11
Return a11 U RECURSIVE-
ACTIVITY- SELECTOR (s, f,
11, 11)
k 0 1 2 3 4 5 6 7 8 9 10 11
sk - 1 3 0 5 3 5 6 8 8 2 12
fk 0 4 5 6 7 8 9 10 11 12 14 16
Created by Sumita Das

11.  RECURSIVE-ACTIVITY- SELECTOR (s, f, 11, 11)
returns Ø.
 Resulting set of selected activities is {a1, a4 a8, a11}
Created by Sumita Das

12. References
 Introduction to Algorithms 2nd ,Cormen, Leiserson,
Rivest and Stein, The MIT Press, 2001.
 Introduction to Design & Analysis Computer Algorithm
3rd, Sara Baase, Allen Van Gelder, Adison-Wesley, 2000.
Created by Sumita Das