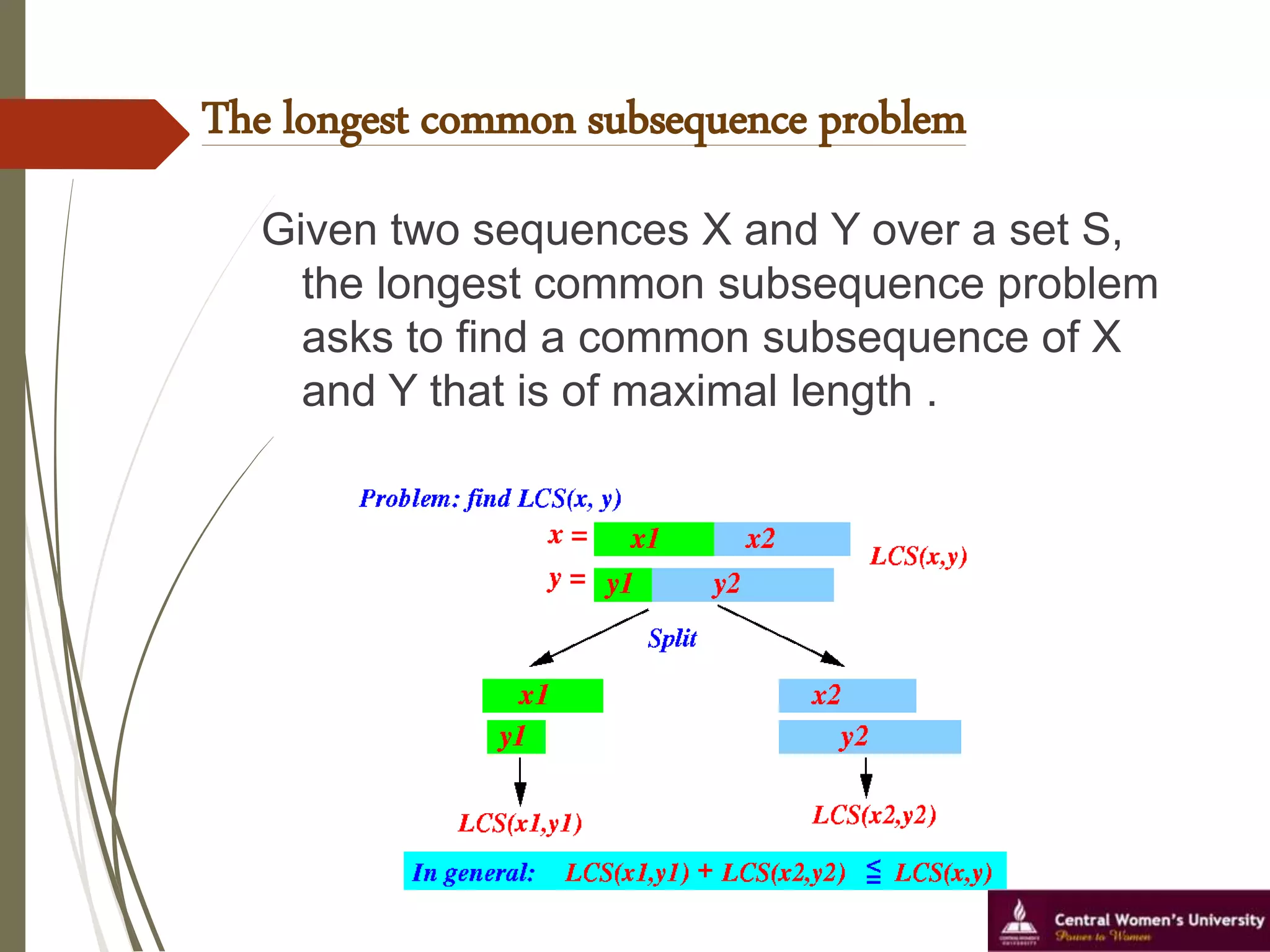
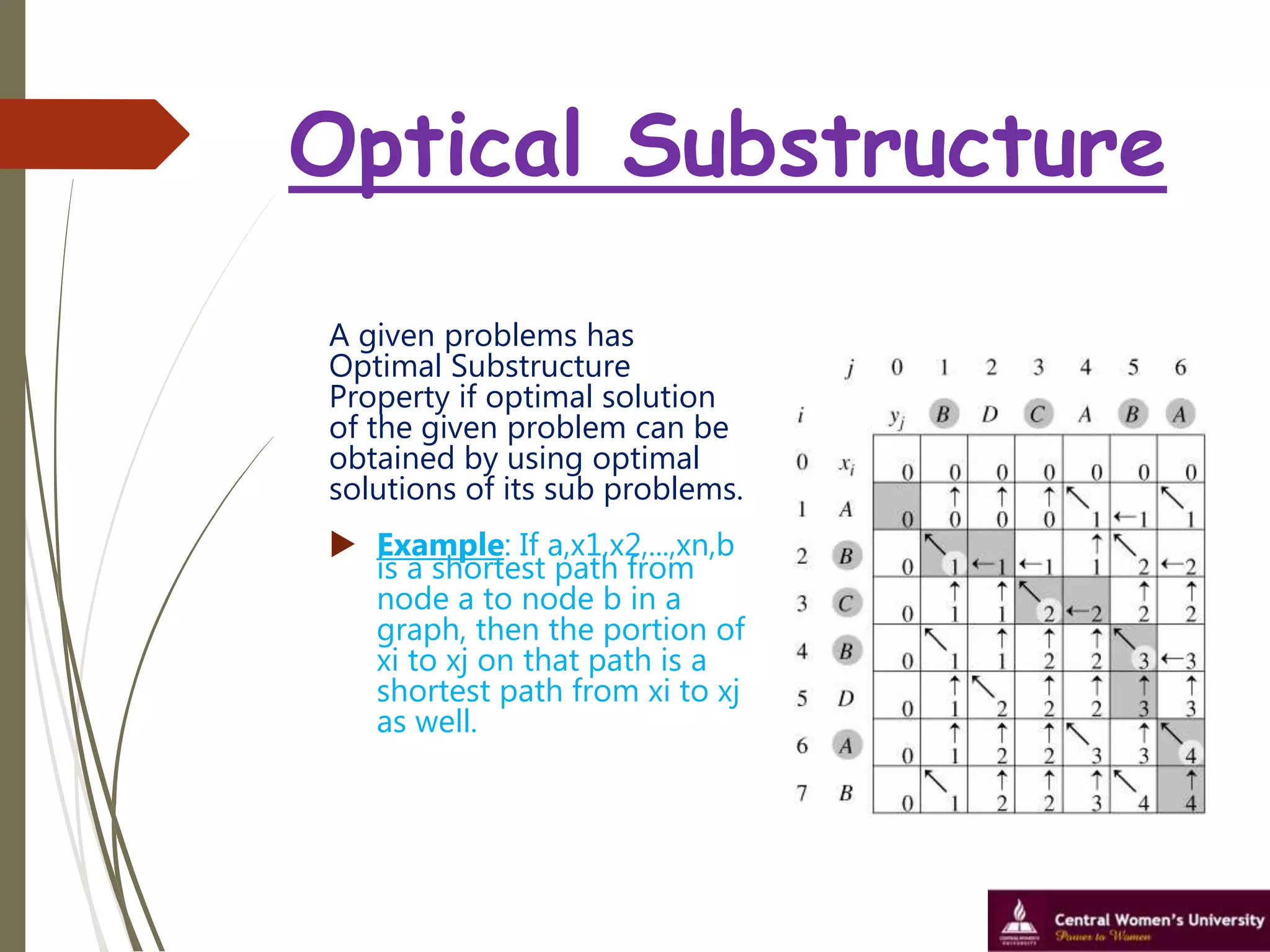
This document discusses the longest common subsequence problem. It defines a longest common subsequence as a sequence that appears in the same relative order in two strings, but not necessarily contiguously. It presents an example longest common subsequence of length 4 between two strings of lengths 6 and 7. It describes a dynamic programming algorithm that runs in O(mn) time, where m and n are the lengths of the input strings, to find the longest common subsequence.

1. LONGEST COMMON
SUBSEQUENCE
1

2. z
Contents
1. Longest Common Subsequence
2. Example
3. Analysis
4. Algorithm
5. The longest common subsequence
problem
6. Naive Solution
7. Optical Substructure
8. Recursive Solution
9. Applications
10. Complexity

3. Longest Common
SubsequenceA longest subsequence is a sequence that
appears in the same relative order, but
not necessarily contiguous(not sub-
string) in both the string.

4. Example
4
String A = "acbaed";
String B = "abcadf";
Longest Common Subsequence(LCS): acad, Length: 4

5. Analysis
We have two nested loops
– The outer one repeats n times
– The inner one repeats m times
– A constant amount of work is done
inside each repetition of the inner loop
– Thus, the total running time is O(nm)
5

6. Algorithm
Algorithm LCS(X,Y ):
Input: Strings X and Y with m and n elements, respectively
Output: For i = 0,...,m; j = 0,...,n, the length C[i, j] of a longest string that is a
subsequence of both the strings.
for i =0 to m
c[i,0] = 0
for j =0 to n
c[0,j] = 0
for i =0 to m
for j =0 to n do
if x i = y j then
c[i, j] = c[i-1, j-1] + 1
else
L[i, j] = max { c[i-1, j] , c[i, j-1]}
return c
6

7. The longest common subsequence problem
Given two sequences X and Y over a set S,
the longest common subsequence problem
asks to find a common subsequence of X
and Y that is of maximal length .

8. Naive Solution
Let X be a sequence of length m,
and Y a sequence of length n.
Check for every subsequence of X
whether it is a subsequence of Y, and
return the longest common
subsequence found.
There are 2 m subsequences of X.
Testing a sequences whether or not it
is a subsequence

9. Optical Substructure
A given problems has
Optimal Substructure
Property if optimal solution
of the given problem can be
obtained by using optimal
solutions of its sub problems.
 Example: If a,x1,x2,...,xn,b
is a shortest path from
node a to node b in a
graph, then the portion of
xi to xj on that path is a
shortest path from xi to xj
as well.

10. Recursive Solution
Start comparing strings in reverse order one character at
a time.
Now we have 2 cases -
 Both characters are same:
Add 1 to the result and remove the last character
from both the strings.
 Both characters are different:
Remove the last character of String and then return
the max from returns of both recursive calls.

11. Applications
1. Knapsack problem.
2. Mathematical optimization problems.
3. Matrix chain multiplication
4. Longest common sequence.
5. Flight control.

12. Complexity
Complexity of Longest Common
Subsequence is O(mn).
Where m and n are lengths of the
two Strings.