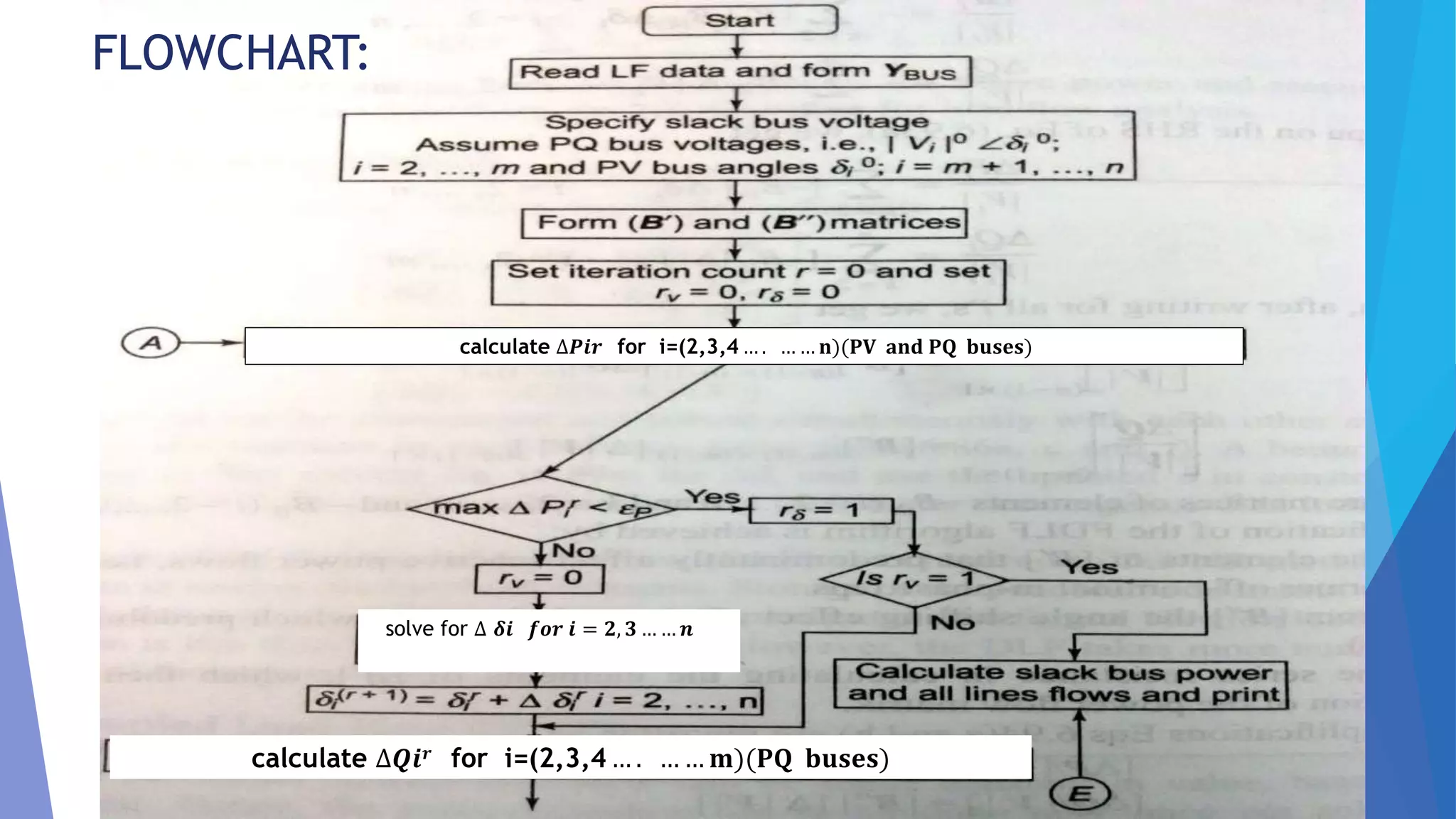
The document discusses the Fast Decoupled Load Flow (FDLF) method for solving load flow problems. FDLF is based on the Newton-Raphson method but further simplifies the load flow equations by assuming that active power changes are more sensitive to voltage angle changes and reactive power changes are more sensitive to voltage magnitude changes. This allows the Jacobian matrix to be separated into two square submatrices related to voltage angle and magnitude. FDLF requires fewer iterations than Newton-Raphson, has higher reliability, and is faster and uses less storage. The method is physically justifiable and can be used in optimization studies involving multiple load flow solutions.

1. Load Flow Study
Fast Decoupled Load Flow(FDLF)
Presented by-
fs

2. Overview
 Fast decoupled load flow
 Why FDLF?
 Flowchart
 Program
 Output
 Conclusion
 Reference

3. Fast decoupled load flow
 Algorithm is based on Newton-Raphson method.
 When transmission lines has a high X/R ratio, the newton Raphson could be
further simplified.
 Consider the Newton-Raphson load flow equation:
 ∆𝑃 are less sensitive to ∆|𝑉| and more sensitive to ∆𝛿.
 ∆𝑄 are less sensitive to ∆𝛿 and more sensitive to ∆|𝑉| .
 So, N and J elements can be eliminated.
∆𝑃
∆𝑄
=
𝐻 𝑁
𝐽 𝐿
∆𝛿
∆|𝑉|
............(1)

4. cos𝛿𝑖𝑘 ≅ 1, sin𝛿𝑖𝑘 ≅0
G𝑖𝑗 sin𝛿𝑖𝑘<<B𝑖𝑘, and Q𝑖<<B𝑖𝑖|V𝑖|2
With these assumptions H and L are square submatrices of dimension (n-
1) and (m-1) respectively are:
For i = k, H𝑖𝑖=L 𝑖𝑖 ≈
- B𝑖𝑖|V𝑖|2
For i≠ 𝑘, H𝑖𝑘=L 𝑖𝑘 ≈- |V𝑖| |V 𝑘| B𝑖𝑘
With further simplification,the matrix equation for the solution of load
flow by FDLF method are:
∆𝑃/|𝑉| = 𝐵′ ∆𝛿 ………..(2)
∆𝑄/|𝑉| = 𝐵′′ ∆|𝑉| … … … . (3)
Where, B’ and B” are matrices of elements -B𝑖𝑘(i=2,…..n and k=2,….n)
and -B𝑖𝑘(i=2,…..,m and k=2,….,m).

5. Why FDLF?
 For practical accuracies, only 2-5 iterations are required.
 More reliable than NR method
 Speed is 5 times that of NR method
 Storage requirement is 60 percent of NR
 Constant jacobian
 Physically justifiable assumptions

6. FLOWCHART:
calculate ∆𝑷𝒊𝒓 for i=(2,3,4 … . … … 𝐧)(𝐏𝐕 𝐚𝐧𝐝 𝐏𝐐 𝐛𝐮𝐬𝐞𝐬)
solve for ∆ 𝜹𝒊 𝒇𝒐𝒓 𝒊 = 𝟐, 𝟑 … … 𝒏
calculate ∆𝑸𝒊 𝒓 for i=(2,3,4 … . … … 𝐦)(𝐏𝐐 𝐛𝐮𝐬𝐞𝐬)

7. Solve for ∆|Vi| for i=2,3 … . … . m.

8. PROGRAM-
fdlf.txt
OUTPUT-

9. Conclusion
 Due to constant jacobian, defining functions are not sensitive to any humps.
 It can be employed in optimization studies.
 Used for obtaining information of both real and reactive power for multiple
load flow studies.

10. References
 M. A.PAI , Computer Techniques in Power System Analysis.
 D.P. Kothari, Modern Power System Analysis .

11. THANK YOU!!!