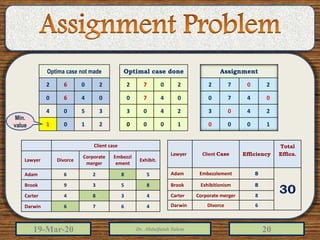
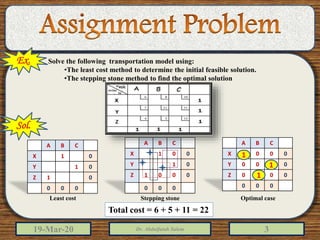
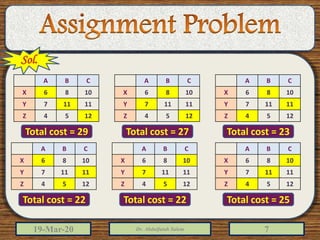
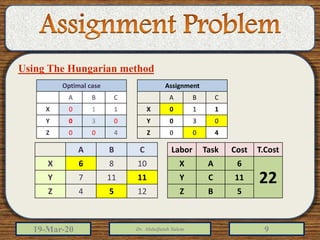
The document discusses the assignment problem and provides examples of solving it using different methods. It can be summarized as: 1) The assignment problem involves allocating tasks or jobs to workers or machines in the most efficient way, often to minimize costs. It has special characteristics as each job can only be assigned to one worker. 2) The document provides examples of solving assignment problems using methods like the least cost method, stepping stone method, and the Hungarian method. 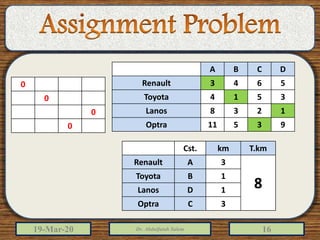3) It also discusses how to model assignment problems as transportation problems and how to solve maximization versions by converting to minimization problems.

2. 19-Mar-20 Dr. Abdulfatah Salem 2
Assignment problem as a special transportation case
Special form of transportation model is the assignment model where.
Supply at each source and demand at each destination limited to one unit.
In a balanced model supply equals demand.
In an unbalanced model supply does not equal demand.

3. 19-Mar-20 Dr. Abdulfatah Salem 3
A B C
X 1 0
Y 1 0
Z 1 0
0 0 0
Total cost = 6 + 5 + 11 = 22
A B C
X 1 0 0
Y 1 0
Z 1 0 0 0
0 0 0
A B C
X 1 0 0 0
Y 0 0 1 0
Z 0 1 0 0
0 0 0
Least cost Stepping stone Optimal case
Ex. Solve the following transportation model using:
•The least cost method to determine the initial feasible solution.
•The stepping stone method to find the optimal solution
Sol.
1
1
1

4. 19-Mar-20 Dr. Abdulfatah Salem 4
The assignment problem refers to the class of linear programming problems
that involve determining the most efficient assignment of :
people to Tasks
salespeople to territories
contracts to bidders
jobs to machines, etc.
The objective is most often to minimize total costs or total time of
performing the tasks at hand.
One important characteristic of assignment problems is that only one job or worker is assigned to one machine or Task.
An example is the problem of a taxi company with 4 taxis and 4 passengers. Which taxi should collect which passenger in order
to minimize costs?
An assignment problem can be viewed as a transportation problem in which:
 The capacity from each source (or person to be assigned) is 1.
 The demand at each destination (or job to be done) is 1.

5. 19-Mar-20 Dr. Abdulfatah Salem 5
1) Find the opportunity cost table by
a) Subtracting the smallest number in each row of the original cost table or matrix
from every number in that row.
b) Then subtracting the smallest number in each column of the table obtained in
part (a) from every number in that column.
2) Test the table resulting from step 1
to see whether an optimal assignment can be made. The procedure is to draw the
minimum number of vertical and horizontal straight lines necessary to cover all zeros in
the table. If the number of lines equals either the number of rows or columns, an optimal
assignment can be made. If the number of lines is less than the number of rows or
columns, we proceed to step 3.
3) Revise the present opportunity cost table
This is done by subtracting the smallest number not covered by a line from every other
uncovered number. This same smallest number is also added to any number(s) lying at
the intersection of the horizontal and vertical lines. We then return to step 2 and
continue the cycle until an optimal assignment is possible.

6. 19-Mar-20 Dr. Abdulfatah Salem 6
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
Ex.
Three computer systems needs to be
installed in the same time by three different
companies, bids for each system are to be
solicited from each company.
Required :
To which company should each system be
assigned.

7. 19-Mar-20 Dr. Abdulfatah Salem 7
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
Sol.
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
Total cost = 29
Total cost = 25Total cost = 22Total cost = 22
Total cost = 23Total cost = 27

8. 19-Mar-20 Dr. Abdulfatah Salem 8
A B C
X 6 8 11
Y 7 11 11
Z 4 5 12
Solution using The Hungarian method
Column
Reduction
Row
Reduction
A B C
X 0 2 5
Y 0 4 4
Z 0 1 8
A B C
X 0 2 5
Y 0 4 4
Z 0 1 8
A B C
X 0 1 1
Y 0 3 0
Z 0 0 4

9. 19-Mar-20 Dr. Abdulfatah Salem 9
Using The Hungarian method
Optimal case
A B C
X 0 1 1
Y 0 3 0
Z 0 0 4
Assignment
A B C
X 0 1 1
Y 0 3 0
Z 0 0 4
A B C
X 6 8 10
Y 7 11 11
Z 4 5 12
Labor Task Cost T.Cost
X A 6
22Y C 11
Z B 5

10. 19-Mar-20 Dr. Abdulfatah Salem 10
Task 1 Task 2 Task 3
Ahmed 11 14 6
Mustafa 8 10 11
Ali 9 12 7
Ex.
Assign
• Three tasks (Task1, Task2, Task3)
to
• Three labors (Ahmed, Mustafa, Ali)
in a way
• That will minimize total costs.

11. 19-Mar-20 Dr. Abdulfatah Salem 11
Task. 1 Task. 2 Task. 3
Ahmed 11 14 6
Mustafa 8 10 11
Ali 9 12 7
Using The Hungarian method
Task. 1 Task. 2 Task. 3
Ahmed 5 8 0
Mustafa 0 2 3
Ali 2 5 0
Column
Reduction
Task. 1 Task. 2 Task. 3
Ahmed 5 8 0
Mustafa 0 2 3
Ali 2 5 0
Task. 1 Task. 2 Task. 3
Ahmed 5 6 0
Mustafa 0 0 3
Ali 2 3 0
Row
Reduction
Sol.

12. 19-Mar-20 Dr. Abdulfatah Salem 12
Task. 1 Task. 2 Task. 3
Ahmed 5 6 0
Mustafa 0 0 3
Ali 2 3 02
Task. 1 Task. 2 Task. 3
Ahmed 3 4 0
Mustafa 0 0 5
Ali 0 1 0
Task. 1 Task. 2 Task. 3
Ahmed 3 4 0
Mustafa 0 0 5
Ali 0 1 0
The no. of lines covering all zeros are 3
Which is equals to the no. of rows
So, the optimality is made
The no. of lines covering all zeros are 2
Which is less than the no. of rows
So, the optimality is not made

13. 19-Mar-20 Dr. Abdulfatah Salem 13
Task. 1 Task. 2 Task. 3
Ahmed 3 4 0
Mustafa 0 0 5
Ali 0 1 0
i. Find a row or column with only one zero cell.
ii. Make the assignment corresponding to that zero cell.
iii. Eliminate that row and column from the table.
iv. Continue until all the assignments have been made.
0
0
0
Ahmed Task. 3
Mustafa Task. 2
Ali Task. 1
Task. 1 Task. 2 Task. 3
6
10
9
Total Cost 9 + 10 + 6 2525

14. 19-Mar-20 Dr. Abdulfatah Salem 14
Ex.
Careem Taxi company has four taxis locating at Smouha area and there are four passengers, A, B,
C and D requiring taxis. The distance between the taxis and the passengers are given in the table
below, in Kilometers'. The Taxi company wishes to assign a taxis to each passenger so that the
distance traveled is a minimum.
A B C D
Renault 3 4 6 5
Toyota 4 1 5 3
Lanos 8 3 2 1
Optra 11 5 3 9

15. 19-Mar-20 Dr. Abdulfatah Salem 15
Raw reduction
0 1 3 2
3 0 4 2
7 2 1 0
8 3 0 6
0
0
0
0
Sol.
Original
3 4 6 5
4 1 5 3
8 3 2 1
11 5 3 9
Column reduction
0 1 3 2
3 0 4 2
7 2 1 0
8 3 0 6
0 1 3 2
3 0 4 2
7 2 1 0
8 3 0 6

16. 19-Mar-20 Dr. Abdulfatah Salem 16
Cst. km T.km
Renault A 3
8
Toyota B 1
Lanos D 1
Optra C 3
A B C D
Renault 3 4 6 5
Toyota 4 1 5 3
Lanos 8 3 2 1
Optra 11 5 3 9
0
0
0
0

17. 19-Mar-20 Dr. Abdulfatah Salem 17
Maximization of the assignment problem :
 Some assignment problems are phrased in terms of maximizing the payoff, profit, or
effectiveness of an assignment instead of minimizing costs.
 It is easy to obtain an equivalent minimization problem by converting all numbers in the
table to opportunity costs.
 This is brought about by subtracting every number in the original payoff table from the
largest single number in that table.
 The transformed entries represent opportunity costs:
 It turns out that minimizing opportunity costs produces the same assignment as the
original maximization problem.
 Once the optimal assignment for this transformed problem has been computed, the total
payoff or profit is found by adding the original payoffs of those cells that are in the optimal
assignment.

18. 19-Mar-20 Dr. Abdulfatah Salem 18
A law firm maintains a large staff of young lawyer who hold the title of junior partner. The firm
concerned with the effective utilization of this personnel resources, seeks some objective means
of making lawyer-to-client assignments. On march 1, four new clients seeking legal assistance
came to the firm. While the current staff is overloads and identifies four junior partners who,
although busy, could possibly be assigned to the cases. Each young lawyer can handle at most
one new client. Furthermore each lawyer differs in skills and specialty interests.
Seeking to maximize the overall effectiveness of the new client assignment, the firm draws up the
following table, in which he rates the estimated effectiveness (of a scale of 1 to 9) of each lawyer
on each new case.
Client case
Lawyer Divorce
Corporate
merger
Embezzlement Exhibitionism
Adam 6 2 8 5
Brook 9 3 5 8
Carter 4 8 3 4
Darwin 6 7 6 4
Ex.

19. 19-Mar-20 Dr. Abdulfatah Salem 19
6 2 8 5
9 3 5 8
4 8 3 4
6 7 6 4
Opportunity Costs table
3 7 1 4
0 6 4 1
5 1 6 5
3 2 3 5
9
Rows reduced cost table
2 6 0 3
0 6 4 1
4 0 5 4
1 0 1 3
Maximum
efficiencySol.
Columns reduced cost table
2 6 0 2
0 6 4 0
4 0 5 3
1 0 1 2

20. 19-Mar-20 Dr. Abdulfatah Salem 20
Optima case not made
2 6 0 2
0 6 4 0
4 0 5 3
1 0 1 2
Optimal case done
2 7 0 2
0 7 4 0
3 0 4 2
0 0 0 1
Min.
value
Assignment
2 7 0 2
0 7 4 0
3 0 4 2
0 0 0 1
Client case
Lawyer Divorce
Corporate
merger
Embezzl
ement
Exhibit.
Adam 6 2 8 5
Brook 9 3 5 8
Carter 4 8 3 4
Darwin 6 7 6 4
Lawyer Client Case Efficiency
Total
Effics.
Adam Embezzlement 8
30
Brook Exhibitionism 8
Carter Corporate merger 8
Darwin Divorce 6

21. GOOD LUCK