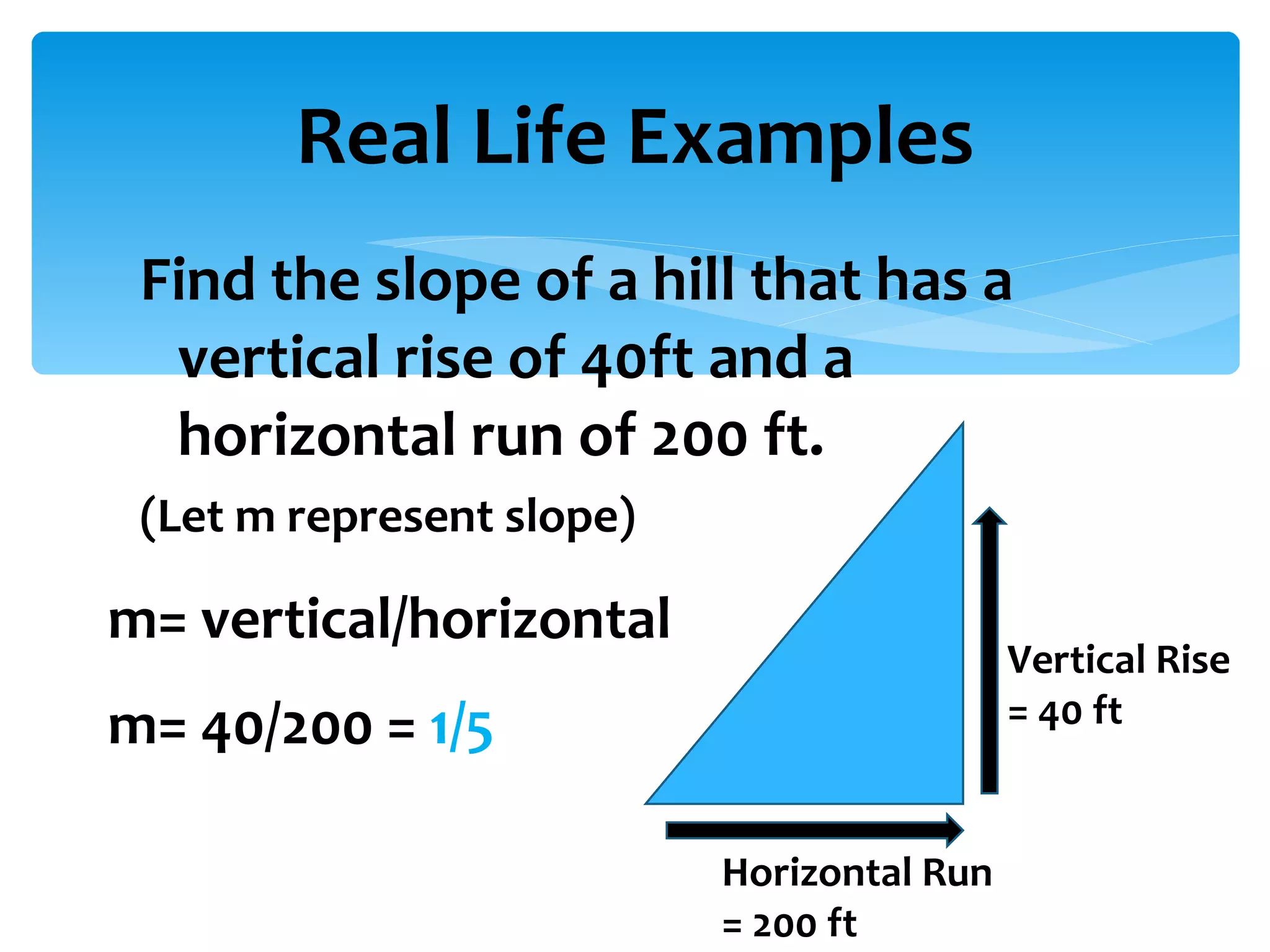
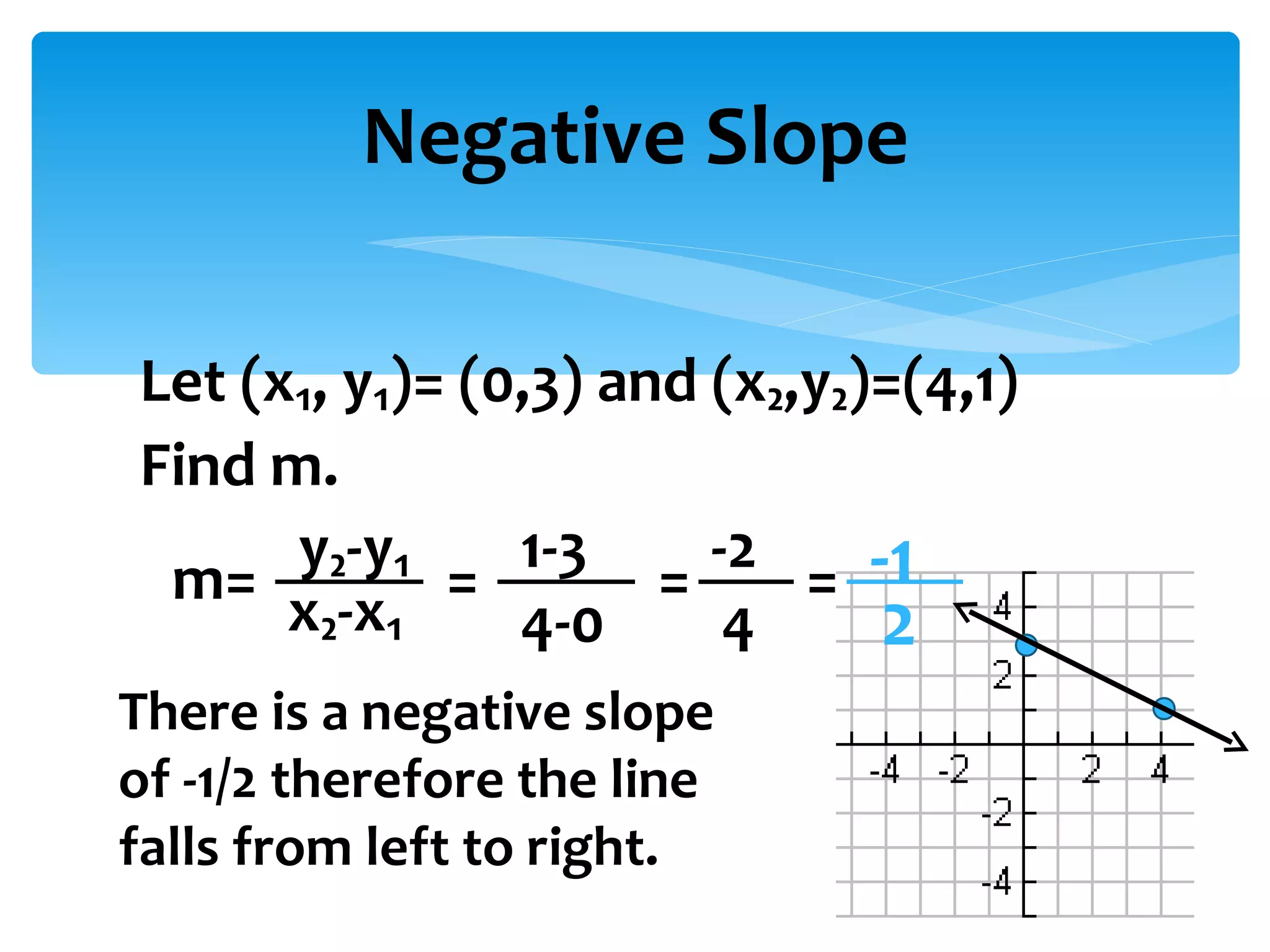
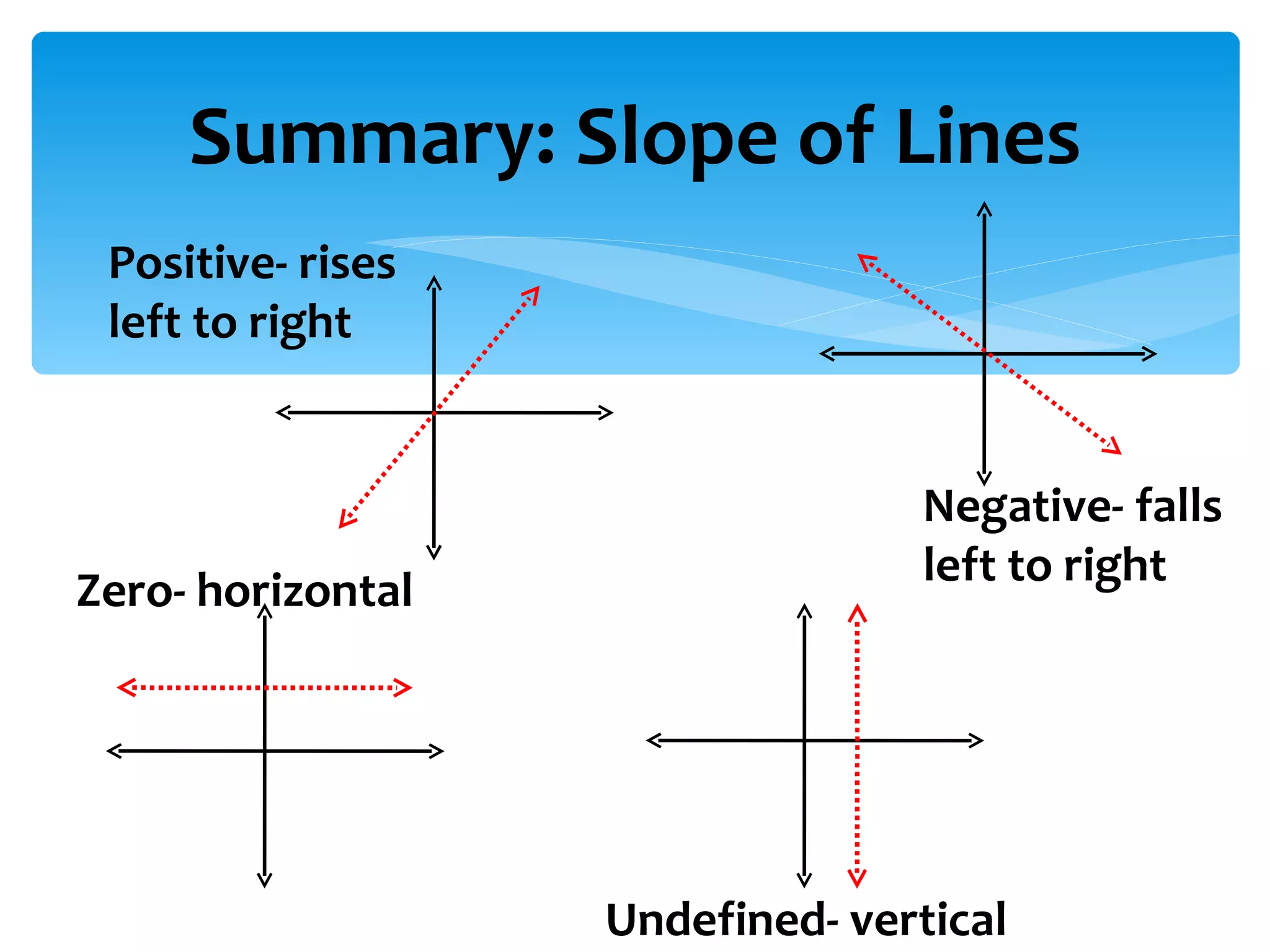
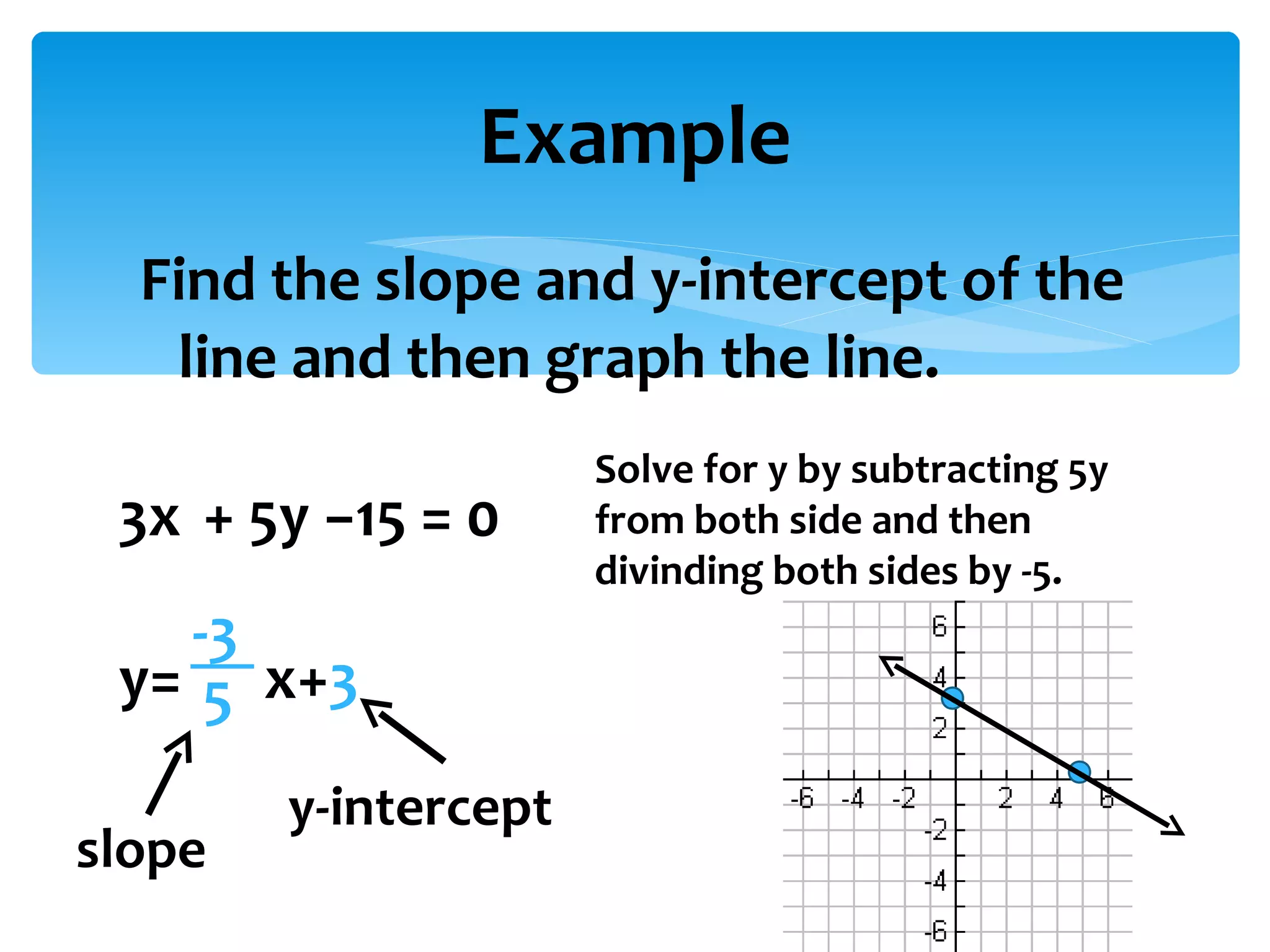
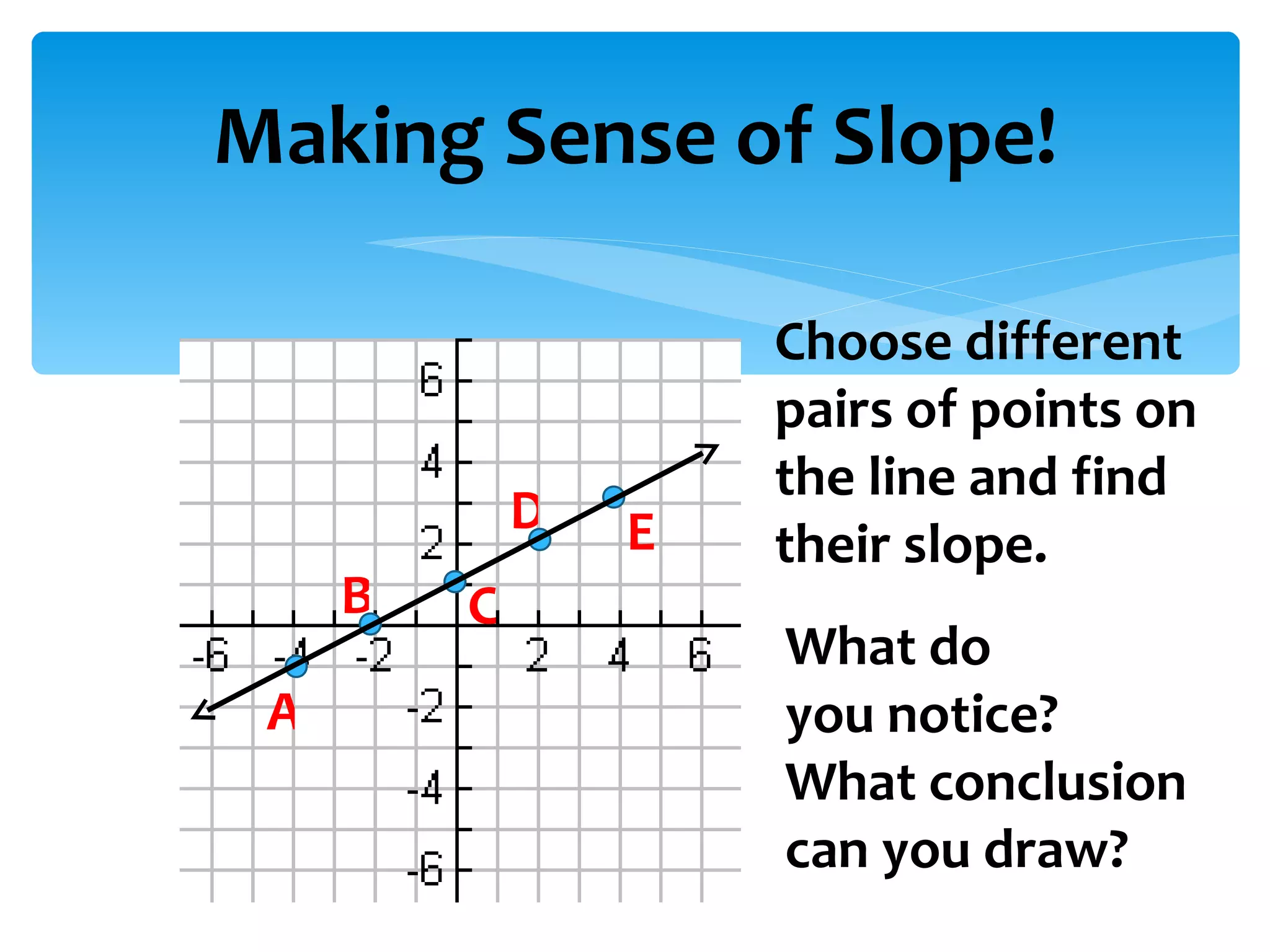
Slope is defined as the ratio of vertical rise to horizontal run between two points on a line. It can be positive, negative, zero, or undefined depending on the orientation of the line. No matter which two points are chosen on the same line, the slope will remain constant. Slope is important in graphing lines and understanding their steepness and direction.

1. Algebra 1- Slope

2. Things that involve slope!

7. Negative Slope Let (x₁, y₁)= (0,3) and (x₂,y₂)=(4,1) Find m. y₂-y₁ x₂-x₁ m= = 1-3 4-0 = 4 -2 = -1 There is a negative slope of -1/2 therefore the line falls from left to right. 2

10. Summary: Slope of Lines Positive- rises left to right Negative- falls left to right Zero- horizontal Undefined- vertical

14. Making Sense of Slope! A D C B E Choose different pairs of points on the line and find their slope. What do you notice? What conclusion can you draw?

15. Making Sense of Slope! Anwsers mAB= mBC= mCD= mDE= 1 2 1 2 1 2 1 2 Now, based on the conclusion that the slope is ½ between each set of points, complete the sentence: No matter what pair of points you choose on a line, the ______ remains constant. *slope

16. The Slope of the Road The slope of the road is the vertical rise divided by the horizontal run. If the vertical rise is 24 feet for a horizontal run of 1 mile, determine the slope of the road. *Hint- 1 mile=5280 feet 24ft 24ft 1 1mi 5280ft 220 = = *This means that for every 1ft that you move up, you also move 220ft forward.