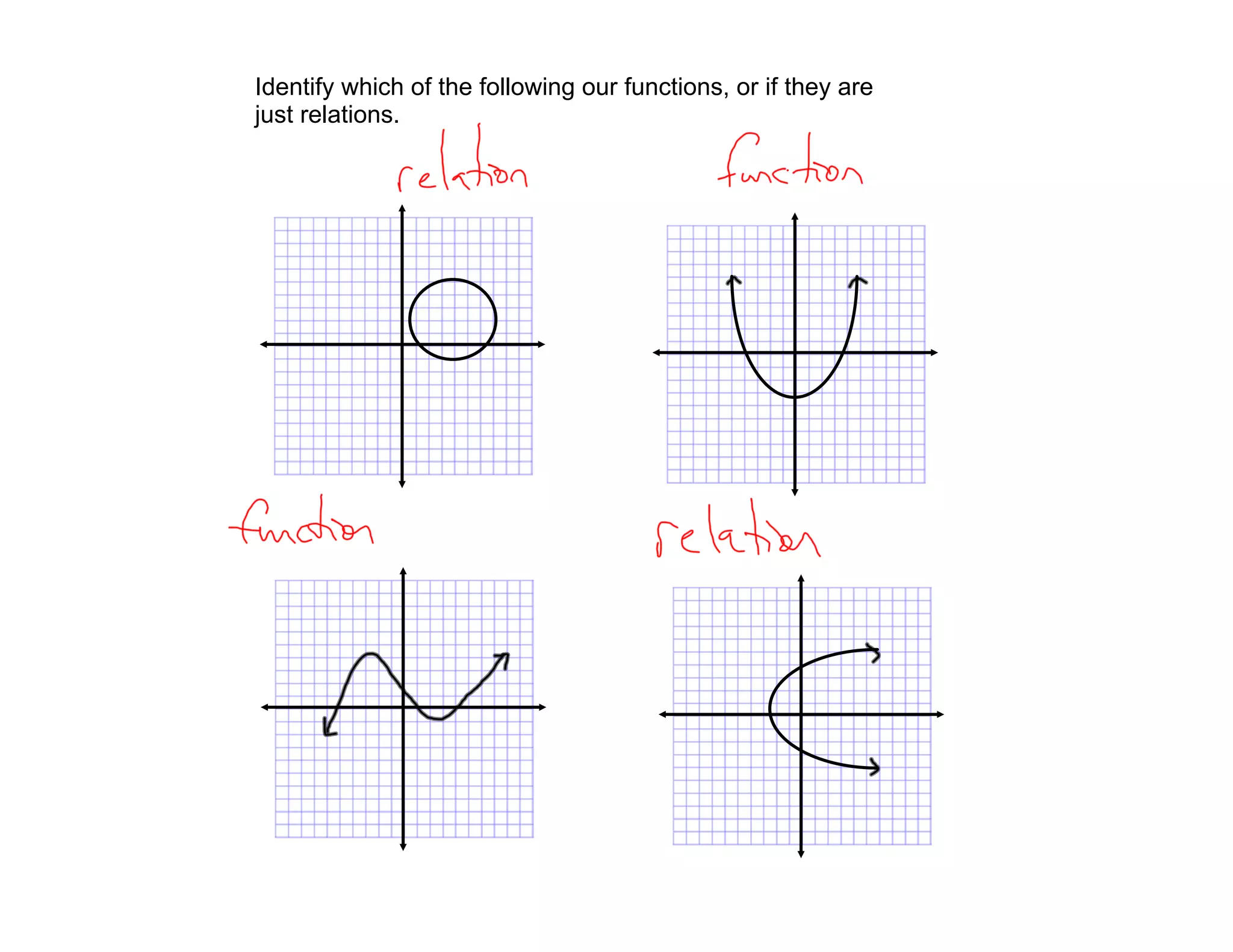
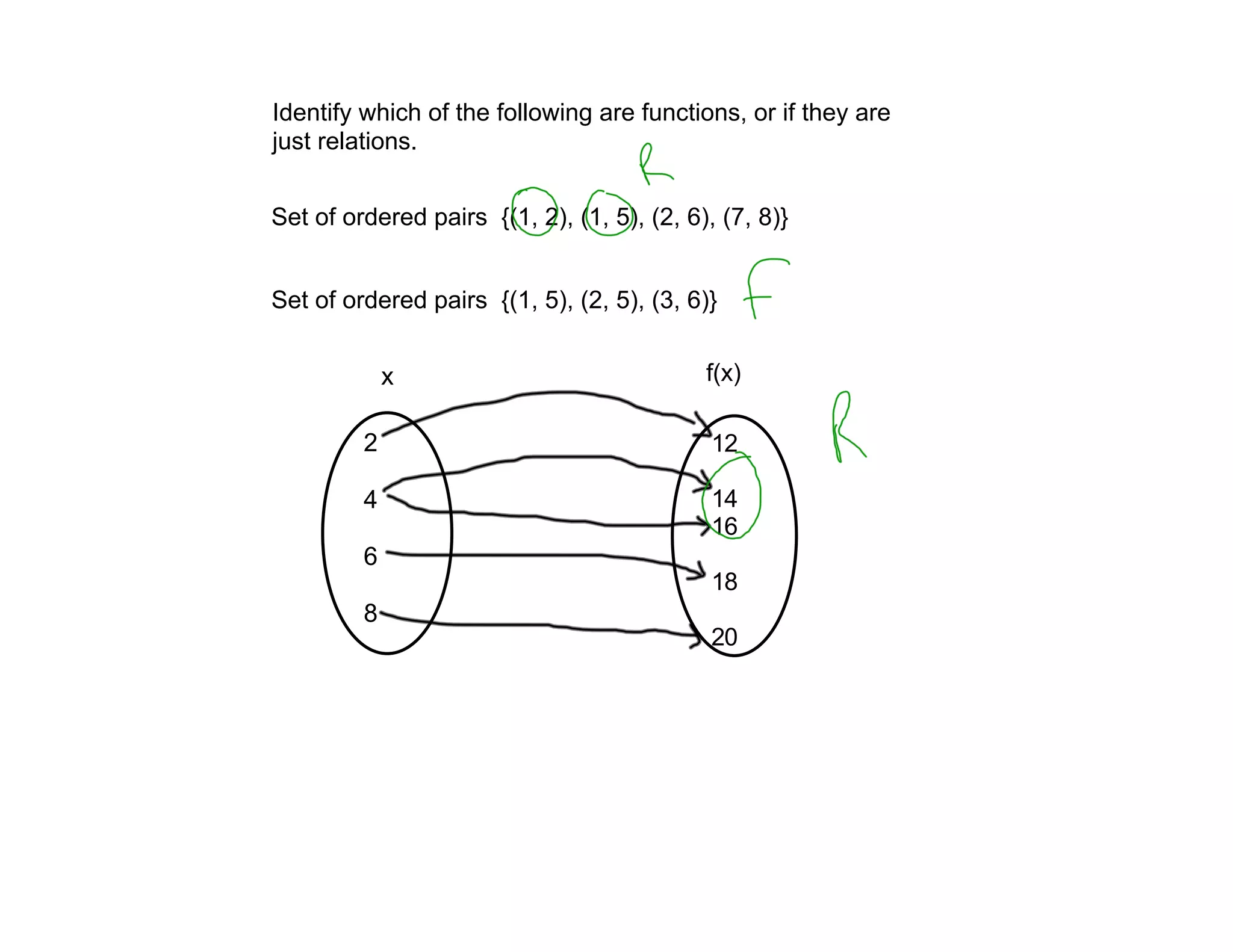
This document defines and provides examples of functions. It discusses: - Functions are relations where each input has exactly one output - The vertical line test to determine if a relation is a function - Common operations on functions like addition, subtraction, multiplication, and division - Composite functions which take the output of one function as the input of another - Examples of evaluating composite functions and performing operations on functions

1. Functions

2. Relation - A set of ordered pairs x and y
x is the input and y is the output
Function - A relation in which each x(input) value has exactly one y
value(output)
Example
2
The function f(x) = x + 1
2
x = 1 then f(1) = 1 2 + 1 = 2
x = 2 then f(2) = 2 + 1 = 5
and so on
Some other common letters used to represent functions are:
g(x), h(x), t(x), s(x)

3. The Verticle Line Test
Sweep a vertical line across the
graph of the function. If the line
crosses the graph more than
once it is not a function, only a
relation.

4. Identify which of the following our functions, or if they are
just relations.

5. Identify which of the following are functions, or if they are
just relations.
Set of ordered pairs {(1, 2), (1, 5), (2, 6), (7, 8)}
Set of ordered pairs {(1, 5), (2, 5), (3, 6)}
x f(x)
2 12
4 14
16
6
18
8
20

6. Operations on Functions
+ - * ÷
Commutativity
+ •
When Adding or Multipyling functions, order in which you put them
in doesn't matter, this is called the Commutative Law.
– /
When Subtracting or Dividing, order in which you put them in does
matter because it can result in different answers.

7. Operations on Functions
= =
= =
= =
= =
= =

8. Composite Functions
Take the output of one function and use it as an input for
another function
Example
(f g)(x) = f(g(x)) Means to find the output for the function of g(x)
° and use it as the input for the function f(x)
2 3
f(x) = 2x + 1 g(x) = x
3 3 2 6
(f ° g)(x) = f(x ) = 2(x ) + 1 = 2x + 1
Or using numbers
Find (f ° g)(x) when x = 3

9. ° Example
f(x) = (x + 1)(x) h(x) = 2x
Find and expression in terms of x for
(h ° f)(x) , then calculate the output for x = 2
Calculate the output for
f(h(x)) when x=2

10. Given the functions f and g such that
f = {(2, 6)(3, 7)(4, 7)}
g = {(6, 10), (7, 12)}
find
a) f(2)
b) g(7)
c) g(f(2))
d) 2g(f(4)) - f(3)

11. Example
2
f(x) = 3x + 2 g(x) = x
find
a) f(g(x))
b) g(g(x))
c) g(2)
f(3)
d) 2f(4) - f(1)
3g(2)

12. Assignment
Exercise 51
1-8, and 8