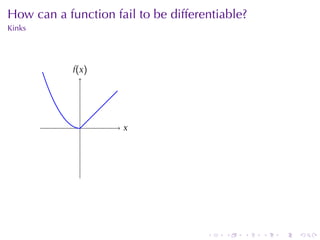
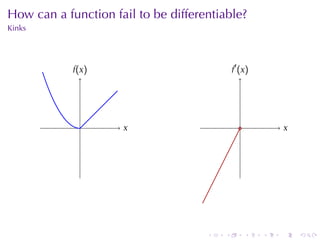
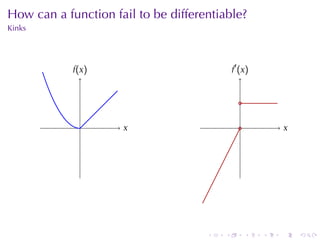
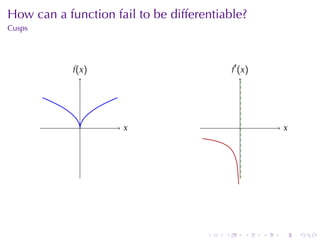
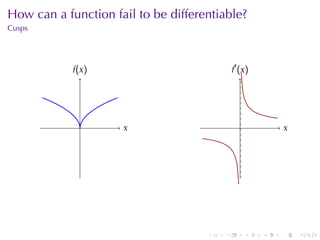
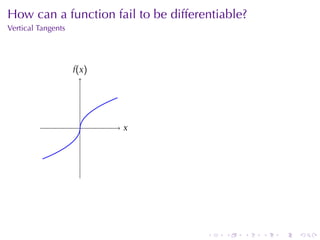
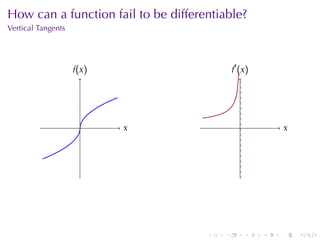
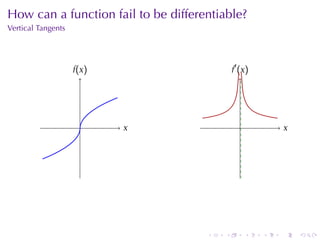
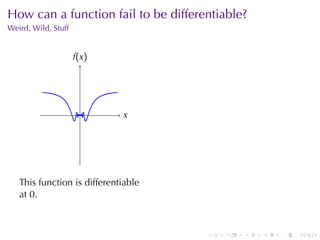
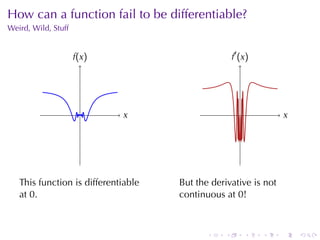
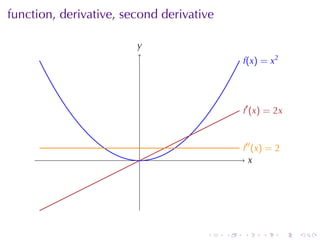
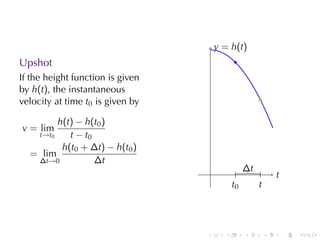
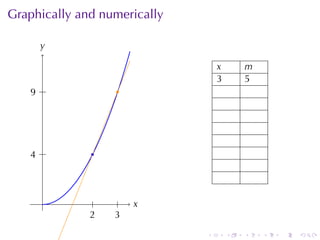
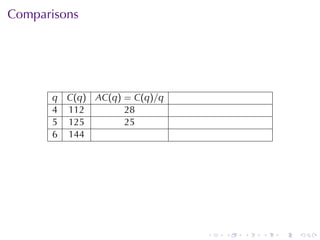
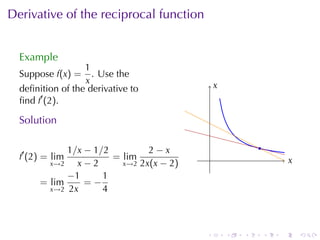
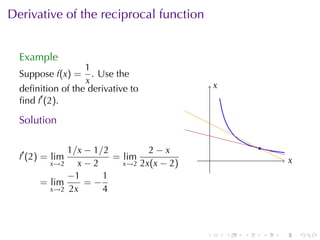
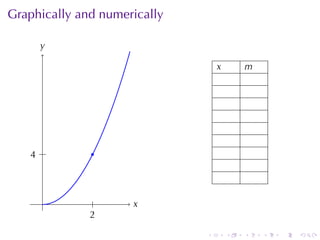
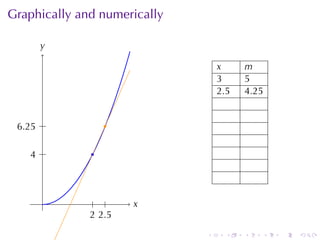
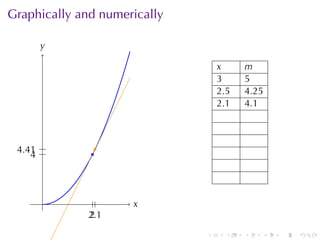
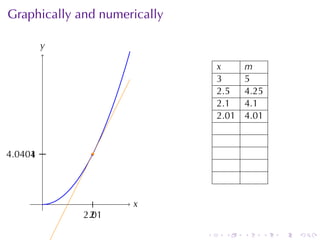
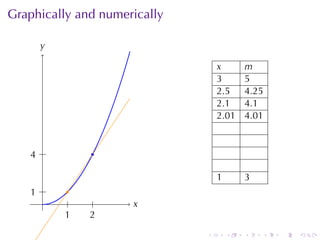
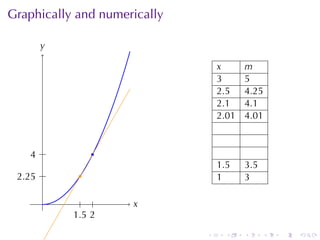
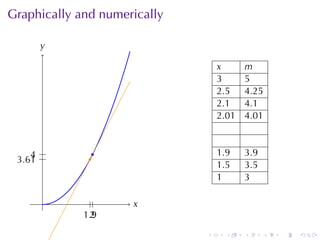
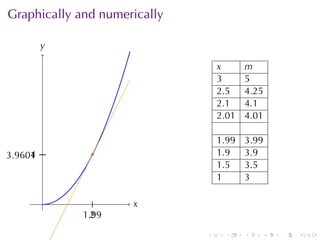
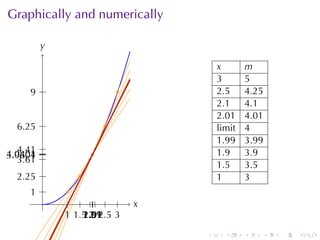
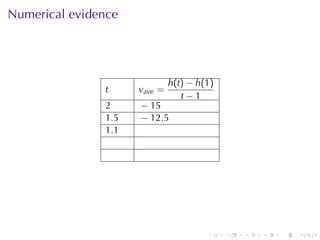
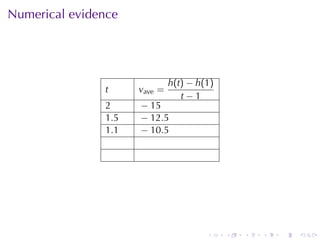
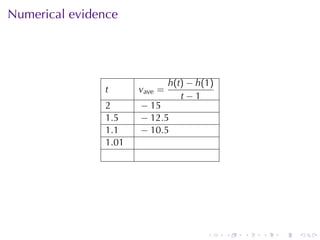
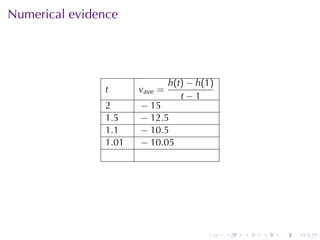
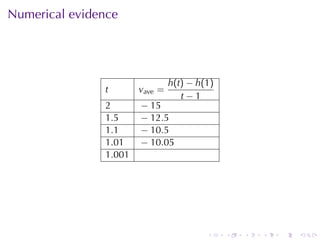
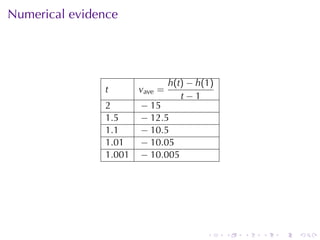
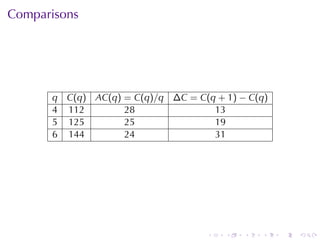
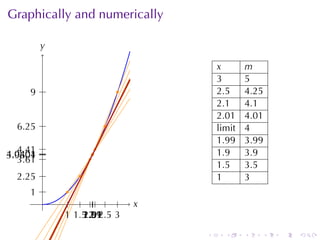
The document appears to be lecture notes for a calculus class that covers several topics: - Defining the derivative and discussing rates of change, tangent lines, velocity, population growth, and marginal costs. - Worked examples are provided for finding the slope of a tangent line, instantaneous velocity, instantaneous population growth rate, and marginal cost of production. - Numerical approximations are used to estimate some values when exact solutions are difficult to obtain analytically.

1. . . . . . .
Section 2.1
The Derivative and Rates of Change
V63.0121.034, Calculus I
September 23, 2009
Announcements
WebAssignments due Monday. Email me if you need an
extension for Yom Kippur.

2. . . . . . .
Regarding WebAssign
We feel your pain

3. . . . . . .
Explanations
From the syllabus:
Graders will be expecting you to express your ideas
clearly, legibly, and completely, often requiring
complete English sentences rather than merely just a
long string of equations or unconnected mathematical
expressions. This means you could lose points for
unexplained answers.

4. . . . . . .
Rubric
Points Description of Work
3 Work is completely accurate and essentially perfect.
Work is thoroughly developed, neat, and easy to read.
Complete sentences are used.
2 Work is good, but incompletely developed, hard to
read, unexplained, or jumbled. Answers which are
not explained, even if correct, will generally receive 2
points. Work contains “right idea” but is flawed.
1 Work is sketchy. There is some correct work, but most
of work is incorrect.
0 Work minimal or non-existent. Solution is completely
incorrect.

5. . . . . . .
Outline
Rates of Change
Tangent Lines
Velocity
Population growth
Marginal costs
The derivative, defined
Derivatives of (some) power functions
What does f tell you about f′
?
How can a function fail to be differentiable?
Other notations
The second derivative

6. . . . . . .
The tangent problem
Problem
Given a curve and a point on the curve, find the slope of the line
tangent to the curve at that point.

7. . . . . . .
The tangent problem
Problem
Given a curve and a point on the curve, find the slope of the line
tangent to the curve at that point.
Example
Find the slope of the line tangent to the curve y = x2
at the point
(2, 4).

8. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
x m

9. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.3
..9
x m
3 5

10. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.2.5
..6.25
x m
3 5
2.5 4.25

11. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.2.1
..4.41
x m
3 5
2.5 4.25
2.1 4.1

12. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 ..
.
.2.01
..4.0401
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01

13. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.1
..1
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
1 3

14. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.1.5
..2.25
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
1.5 3.5
1 3

15. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.1.9
..3.61
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
1.9 3.9
1.5 3.5
1 3

16. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 ..
.
.1.99
..3.9601
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
1.99 3.99
1.9 3.9
1.5 3.5
1 3

17. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.3
..9
.
.
.2.5
..6.25
.
.
.2.1
..4.41 .
.
.2.01
..4.0401
.
.
.1
..1
.
.
.1.5
..2.25
.
.
.1.9
..3.61
.
.
.1.99
..3.9601
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
limit 4
1.99 3.99
1.9 3.9
1.5 3.5
1 3

18. . . . . . .
The tangent problem
Problem
Given a curve and a point on the curve, find the slope of the line
tangent to the curve at that point.
Example
Find the slope of the line tangent to the curve y = x2
at the point
(2, 4).
Upshot
If the curve is given by y = f(x), and the point on the curve is
(a, f(a)), then the slope of the tangent line is given by
mtangent = lim
x→a
f(x) − f(a)
x − a

19. . . . . . .
Velocity
Problem
Given the position function of a moving object, find the velocity
of the object at a certain instant in time.
Example
Drop a ball off the roof of the Silver Center so that its height can
be described by
h(t) = 50 − 5t2
where t is seconds after dropping it and h is meters above the
ground. How fast is it falling one second after we drop it?

20. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15

21. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5

22. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5

23. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1

24. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1 − 10.5

25. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1 − 10.5
1.01

26. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1 − 10.5
1.01 − 10.05

27. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1 − 10.5
1.01 − 10.05
1.001

28. . . . . . .
Numerical evidence
t vave =
h(t) − h(1)
t − 1
2 − 15
1.5 − 12.5
1.1 − 10.5
1.01 − 10.05
1.001 − 10.005

29. . . . . . .
Velocity
Problem
Given the position function of a moving object, find the velocity
of the object at a certain instant in time.
Example
Drop a ball off the roof of the Silver Center so that its height can
be described by
h(t) = 50 − 5t2
where t is seconds after dropping it and h is meters above the
ground. How fast is it falling one second after we drop it?
Solution
The answer is
v = lim
t→1
(50 − 5t2) − 45
t − 1
= lim
t→1
5 − 5t2
t − 1
= lim
t→1
5(1 − t)(1 + t)
t − 1
= (−5) lim
t→1
(1 + t) = −5 · 2 = −10

30. . . . . . .
Upshot
If the height function is given
by h(t), the instantaneous
velocity at time t0 is given by
v = lim
t→t0
h(t) − h(t0)
t − t0
= lim
∆t→0
h(t0 + ∆t) − h(t0)
∆t
. .t
.y = h(t)
.
.
.
.t0
.
.t
.∆t

31. . . . . . .
Population growth
Problem
Given the population function of a group of organisms, find the
rate of growth of the population at a particular instant.

32. . . . . . .
Population growth
Problem
Given the population function of a group of organisms, find the
rate of growth of the population at a particular instant.
Example
Suppose the population of fish in the East River is given by the
function
P(t) =
3et
1 + et
where t is in years since 2000 and P is in millions of fish. Is the
fish population growing fastest in 1990, 2000, or 2010? (Estimate
numerically)?

33. . . . . . .
Derivation
Let ∆t be an increment in time and ∆P the corresponding change
in population:
∆P = P(t + ∆t) − P(t)
This depends on ∆t, so we want
lim
∆t→0
∆P
∆t
= lim
∆t→0
1
∆t
(
3et+∆t
1 + et+∆t
−
3et
1 + et
)

34. . . . . . .
Derivation
Let ∆t be an increment in time and ∆P the corresponding change
in population:
∆P = P(t + ∆t) − P(t)
This depends on ∆t, so we want
lim
∆t→0
∆P
∆t
= lim
∆t→0
1
∆t
(
3et+∆t
1 + et+∆t
−
3et
1 + et
)
Too hard! Try a small ∆t to approximate.

35. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈

36. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈ 0.000136

37. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈ 0.000136
r2000 ≈
P(0.1) − P(0)
0.1
≈

38. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈ 0.000136
r2000 ≈
P(0.1) − P(0)
0.1
≈ 0.75

39. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈ 0.000136
r2000 ≈
P(0.1) − P(0)
0.1
≈ 0.75
r2010 ≈
P(10 + 0.1) − P(10)
0.1
≈

40. . . . . . .
Numerical evidence
r1990 ≈
P(−10 + 0.1) − P(−10)
0.1
≈ 0.000136
r2000 ≈
P(0.1) − P(0)
0.1
≈ 0.75
r2010 ≈
P(10 + 0.1) − P(10)
0.1
≈ 0.000136

41. . . . . . .
Population growth
Problem
Given the population function of a group of organisms, find the
rate of growth of the population at a particular instant.
Example
Suppose the population of fish in the East River is given by the
function
P(t) =
3et
1 + et
where t is in years since 2000 and P is in millions of fish. Is the
fish population growing fastest in 1990, 2000, or 2010? (Estimate
numerically)?
Solution
The estimated rates of growth are 0.000136, 0.75, and 0.000136.

42. . . . . . .
Upshot
The instantaneous population growth is given by
lim
∆t→0
P(t + ∆t) − P(t)
∆t

43. . . . . . .
Marginal costs
Problem
Given the production cost of a good, find the marginal cost of
production after having produced a certain quantity.

44. . . . . . .
Marginal costs
Problem
Given the production cost of a good, find the marginal cost of
production after having produced a certain quantity.
Example
Suppose the cost of producing q tons of rice on our paddy in a
year is
C(q) = q3
− 12q2
+ 60q
We are currently producing 5 tons a year. Should we change that?

45. . . . . . .
Comparisons
q C(q)
4
5
6

46. . . . . . .
Comparisons
q C(q)
4 112
5
6

47. . . . . . .
Comparisons
q C(q)
4 112
5 125
6

48. . . . . . .
Comparisons
q C(q)
4 112
5 125
6 144

49. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q
4 112
5 125
6 144

50. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q
4 112 28
5 125
6 144

51. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q
4 112 28
5 125 25
6 144

52. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q
4 112 28
5 125 25
6 144 24

53. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q ∆C = C(q + 1) − C(q)
4 112 28
5 125 25
6 144 24

54. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q ∆C = C(q + 1) − C(q)
4 112 28 13
5 125 25
6 144 24

55. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q ∆C = C(q + 1) − C(q)
4 112 28 13
5 125 25 19
6 144 24

56. . . . . . .
Comparisons
q C(q) AC(q) = C(q)/q ∆C = C(q + 1) − C(q)
4 112 28 13
5 125 25 19
6 144 24 31

57. . . . . . .
Marginal costs
Problem
Given the production cost of a good, find the marginal cost of
production after having produced a certain quantity.
Example
Suppose the cost of producing q tons of rice on our paddy in a
year is
C(q) = q3
− 12q2
+ 60q
We are currently producing 5 tons a year. Should we change that?
Example
If q = 5, then C = 125, ∆C = 19, while AC = 25. So we should
produce more to lower average costs.

58. . . . . . .
Upshot
The incremental cost
∆C = C(q + 1) − C(q)
is useful, but depends on units.

59. . . . . . .
Upshot
The incremental cost
∆C = C(q + 1) − C(q)
is useful, but depends on units.
The marginal cost after producing q given by
MC = lim
∆q→0
C(q + ∆q) − C(q)
∆q
is more useful since it’s unit-independent.

60. . . . . . .
Outline
Rates of Change
Tangent Lines
Velocity
Population growth
Marginal costs
The derivative, defined
Derivatives of (some) power functions
What does f tell you about f′
?
How can a function fail to be differentiable?
Other notations
The second derivative

61. . . . . . .
The definition
All of these rates of change are found the same way!

62. . . . . . .
The definition
All of these rates of change are found the same way!
Definition
Let f be a function and a a point in the domain of f. If the limit
f′
(a) = lim
h→0
f(a + h) − f(a)
h
exists, the function is said to be differentiable at a and f′
(a) is the
derivative of f at a.

63. . . . . . .
Derivative of the squaring function
Example
Suppose f(x) = x2
. Use the definition of derivative to find f′
(a).

64. . . . . . .
Derivative of the squaring function
Example
Suppose f(x) = x2
. Use the definition of derivative to find f′
(a).
Solution
f′
(a) = lim
h→0
f(a + h) − f(a)
h
= lim
h→0
(a + h)2 − a2
h
= lim
h→0
(a2 + 2ah + h2
) − a2
h
= lim
h→0
2ah + h2
h
= lim
h→0
(2a + h) = 2a.

65. . . . . . .
Derivative of the reciprocal function
Example
Suppose f(x) =
1
x
. Use the
definition of the derivative to
find f′
(2).

66. . . . . . .
Derivative of the reciprocal function
Example
Suppose f(x) =
1
x
. Use the
definition of the derivative to
find f′
(2).
Solution
f′
(2) = lim
x→2
1/x − 1/2
x − 2
= lim
x→2
2 − x
2x(x − 2)
= lim
x→2
−1
2x
= −
1
4
. .x
.x
.

67. . . . . . .
The Sure-Fire Sally Rule (SFSR) for adding Fractions
In anticipation of the question, “How did you get that?”
a
b
±
c
d
=
ad ± bc
bd
So
1
x
−
1
2
x − 2
=
2 − x
2x
x − 2
=
2 − x
2x(x − 2)

68. . . . . . .
The Sure-Fire Sally Rule (SFSR) for adding Fractions
In anticipation of the question, “How did you get that?”
a
b
±
c
d
=
ad ± bc
bd
So
1
x
−
1
2
x − 2
=
2 − x
2x
x − 2
=
2 − x
2x(x − 2)

69. . . . . . .
What does f tell you about f′
?
If f is a function, we can compute the derivative f′
(x) at each
point x where f is differentiable, and come up with another
function, the derivative function.
What can we say about this function f′
?

70. . . . . . .
What does f tell you about f′
?
If f is a function, we can compute the derivative f′
(x) at each
point x where f is differentiable, and come up with another
function, the derivative function.
What can we say about this function f′
?
If f is decreasing on an interval, f′
is negative (well,
nonpositive) on that interval

71. . . . . . .
Derivative of the reciprocal function
Example
Suppose f(x) =
1
x
. Use the
definition of the derivative to
find f′
(2).
Solution
f′
(2) = lim
x→2
1/x − 1/2
x − 2
= lim
x→2
2 − x
2x(x − 2)
= lim
x→2
−1
2x
= −
1
4
. .x
.x
.

72. . . . . . .
What does f tell you about f′
?
If f is a function, we can compute the derivative f′
(x) at each
point x where f is differentiable, and come up with another
function, the derivative function.
What can we say about this function f′
?
If f is decreasing on an interval, f′
is negative (well,
nonpositive) on that interval
If f is increasing on an interval, f′
is positive (well,
nonnegative) on that interval

73. . . . . . .
Graphically and numerically
. .x
.y
.
.2
..4 .
.
.
.3
..9
.
.
.2.5
..6.25
.
.
.2.1
..4.41 .
.
.2.01
..4.0401
.
.
.1
..1
.
.
.1.5
..2.25
.
.
.1.9
..3.61
.
.
.1.99
..3.9601
x m
3 5
2.5 4.25
2.1 4.1
2.01 4.01
limit 4
1.99 3.99
1.9 3.9
1.5 3.5
1 3

74. . . . . . .
What does f tell you about f′
?
Fact
If f is decreasing on (a, b), then f′
≤ 0 on (a, b).
Proof.
If f is decreasing on (a, b), and ∆x > 0, then
f(x + ∆x) < f(x) =⇒
f(x + ∆x) − f(x)
∆x
< 0

75. . . . . . .
What does f tell you about f′
?
Fact
If f is decreasing on (a, b), then f′
≤ 0 on (a, b).
Proof.
If f is decreasing on (a, b), and ∆x > 0, then
f(x + ∆x) < f(x) =⇒
f(x + ∆x) − f(x)
∆x
< 0
But if ∆x < 0, then x + ∆x < x, and
f(x + ∆x) > f(x) =⇒
f(x + ∆x) − f(x)
∆x
< 0
still!

76. . . . . . .
What does f tell you about f′
?
Fact
If f is decreasing on (a, b), then f′
≤ 0 on (a, b).
Proof.
If f is decreasing on (a, b), and ∆x > 0, then
f(x + ∆x) < f(x) =⇒
f(x + ∆x) − f(x)
∆x
< 0
But if ∆x < 0, then x + ∆x < x, and
f(x + ∆x) > f(x) =⇒
f(x + ∆x) − f(x)
∆x
< 0
still! Either way,
f(x + ∆x) − f(x)
∆x
< 0, so
f′
(x) = lim
∆x→0
f(x + ∆x) − f(x)
∆x
≤ 0

77. . . . . . .
Outline
Rates of Change
Tangent Lines
Velocity
Population growth
Marginal costs
The derivative, defined
Derivatives of (some) power functions
What does f tell you about f′
?
How can a function fail to be differentiable?
Other notations
The second derivative

78. . . . . . .
Differentiability is super-continuity
Theorem
If f is differentiable at a, then f is continuous at a.

79. . . . . . .
Differentiability is super-continuity
Theorem
If f is differentiable at a, then f is continuous at a.
Proof.
We have
lim
x→a
(f(x) − f(a)) = lim
x→a
f(x) − f(a)
x − a
· (x − a)
= lim
x→a
f(x) − f(a)
x − a
· lim
x→a
(x − a)
= f′
(a) · 0 = 0

80. . . . . . .
Differentiability is super-continuity
Theorem
If f is differentiable at a, then f is continuous at a.
Proof.
We have
lim
x→a
(f(x) − f(a)) = lim
x→a
f(x) − f(a)
x − a
· (x − a)
= lim
x→a
f(x) − f(a)
x − a
· lim
x→a
(x − a)
= f′
(a) · 0 = 0
Note the proper use of the limit law: if the factors each have a
limit at a, the limit of the product is the product of the limits.

81. . . . . . .
How can a function fail to be differentiable?
Kinks
. .x
.f(x)

82. . . . . . .
How can a function fail to be differentiable?
Kinks
. .x
.f(x)
. .x
.f′
(x)
.

83. . . . . . .
How can a function fail to be differentiable?
Kinks
. .x
.f(x)
. .x
.f′
(x)
.
.

84. . . . . . .
How can a function fail to be differentiable?
Cusps
. .x
.f(x)

85. . . . . . .
How can a function fail to be differentiable?
Cusps
. .x
.f(x)
. .x
.f′
(x)

86. . . . . . .
How can a function fail to be differentiable?
Cusps
. .x
.f(x)
. .x
.f′
(x)

87. . . . . . .
How can a function fail to be differentiable?
Vertical Tangents
. .x
.f(x)

88. . . . . . .
How can a function fail to be differentiable?
Vertical Tangents
. .x
.f(x)
. .x
.f′
(x)

89. . . . . . .
How can a function fail to be differentiable?
Vertical Tangents
. .x
.f(x)
. .x
.f′
(x)

90. . . . . . .
How can a function fail to be differentiable?
Weird, Wild, Stuff
. .x
.f(x)
This function is differentiable
at 0.

91. . . . . . .
How can a function fail to be differentiable?
Weird, Wild, Stuff
. .x
.f(x)
This function is differentiable
at 0.
. .x
.f′
(x)
But the derivative is not
continuous at 0!

92. . . . . . .
Outline
Rates of Change
Tangent Lines
Velocity
Population growth
Marginal costs
The derivative, defined
Derivatives of (some) power functions
What does f tell you about f′
?
How can a function fail to be differentiable?
Other notations
The second derivative

93. . . . . . .
Notation
Newtonian notation
f′
(x) y′
(x) y′
Leibnizian notation
dy
dx
d
dx
f(x)
df
dx
These all mean the same thing.

94. . . . . . .
Meet the Mathematician: Isaac Newton
English, 1643–1727
Professor at Cambridge
(England)
Philosophiae Naturalis
Principia Mathematica
published 1687

95. . . . . . .
Meet the Mathematician: Gottfried Leibniz
German, 1646–1716
Eminent philosopher as
well as mathematician
Contemporarily
disgraced by the
calculus priority dispute

96. . . . . . .
Outline
Rates of Change
Tangent Lines
Velocity
Population growth
Marginal costs
The derivative, defined
Derivatives of (some) power functions
What does f tell you about f′
?
How can a function fail to be differentiable?
Other notations
The second derivative

97. . . . . . .
The second derivative
If f is a function, so is f′
, and we can seek its derivative.
f′′
= (f′
)′
It measures the rate of change of the rate of change!

98. . . . . . .
The second derivative
If f is a function, so is f′
, and we can seek its derivative.
f′′
= (f′
)′
It measures the rate of change of the rate of change! Leibnizian
notation:
d2
y
dx2
d2
dx2
f(x)
d2
f
dx2

99. . . . . . .
function, derivative, second derivative
. .x
.y
.f(x) = x2
.f′
(x) = 2x
.f′′
(x) = 2