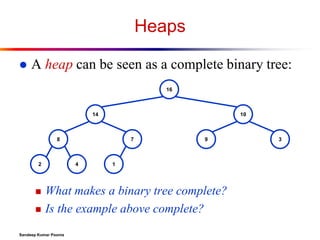
The document discusses algorithms and data structures. It begins with an introduction to merge sort, solving recurrences, and the master theorem for analyzing divide-and-conquer algorithms. It then covers quicksort and heaps. The last part discusses heaps in more detail and provides an example heap representation as a complete binary tree.

1. Algorithms
Sandeep Kumar Poonia
Head Of Dept. CS/IT
B.E., M.Tech., UGC-NET
LM-IAENG, LM-IACSIT,LM-CSTA, LM-AIRCC, LM-SCIEI, AM-UACEE

2. Algorithms
Merge Sort
Solving Recurrences
The Master Theorem
Introduction to heapsort
Quicksort
Sandeep Kumar Poonia

3. Merge Sort
MergeSort(A, left, right) {
if (left < right) {
mid = floor((left + right) / 2);
MergeSort(A, left, mid);
MergeSort(A, mid+1, right);
Merge(A, left, mid, right);
}
}
// Merge() takes two sorted subarrays of A and
// merges them into a single sorted subarray of A
//
(how long should this take?)
Sandeep Kumar Poonia

4. Merge Sort: Example

Show MergeSort() running on the array
A = {10, 5, 7, 6, 1, 4, 8, 3, 2, 9};
Sandeep Kumar Poonia

5. Analysis of Merge Sort
Statement
Effort
MergeSort(A, left, right) {
if (left < right) {
mid = floor((left + right) / 2);
MergeSort(A, left, mid);
MergeSort(A, mid+1, right);
Merge(A, left, mid, right);
}
}
 So T(n) = (1) when n = 1, and
2T(n/2) + (n) when n > 1

So what (more succinctly) is T(n)?
Sandeep Kumar Poonia
T(n)
(1)
(1)
T(n/2)
T(n/2)
(n)

6. Recurrences

The expression:
c
n 1



T ( n)  
n
2T    cn n  1
 2

is a recurrence.

Recurrence: an equation that describes a function
in terms of its value on smaller functions
Sandeep Kumar Poonia

7. Recurrence Examples
0
n0

s ( n)  
c  s(n  1) n  0
0
n0

s ( n)  
n  s(n  1) n  0
c
n 1



T ( n)  
n
2T    c n  1
 2



c
n 1

T ( n)  
 n
aT    cn n  1
 b
Sandeep Kumar Poonia

8. Solving Recurrences
Substitution method
 Iteration method
 Master method

Sandeep Kumar Poonia

9. Solving Recurrences

The substitution method



A.k.a. the “making a good guess method”
Guess the form of the answer, then use induction
to find the constants and show that solution works
Examples:
= 2T(n/2) + (n)  T(n) = (n lg n)
 T(n) = 2T(n/2) + n  ???
 T(n)
Sandeep Kumar Poonia

10. Solving Recurrences

The substitution method



A.k.a. the “making a good guess method”
Guess the form of the answer, then use induction
to find the constants and show that solution works
Examples:
= 2T(n/2) + (n)  T(n) = (n lg n)
 T(n) = 2T(n/2) + n  T(n) = (n lg n)
 T(n) = 2T(n/2 )+ 17) + n  ???
 T(n)
Sandeep Kumar Poonia

11. Solving Recurrences

The substitution method



A.k.a. the “making a good guess method”
Guess the form of the answer, then use induction
to find the constants and show that solution works
Examples:
= 2T(n/2) + (n)  T(n) = (n lg n)
 T(n) = 2T(n/2) + n  T(n) = (n lg n)
 T(n) = 2T(n/2+ 17) + n  (n lg n)
 T(n)
Sandeep Kumar Poonia

12. Solving Recurrences

Another option is the “iteration method”




Expand the recurrence
Work some algebra to express as a summation
Evaluate the summation
We will show several examples
Sandeep Kumar Poonia

13. 0
n0

s ( n)  
c  s(n  1) n  0

s(n) =
c + s(n-1)
c + c + s(n-2)
2c + s(n-2)
2c + c + s(n-3)
3c + s(n-3)
…
kc + s(n-k) = ck + s(n-k)
Sandeep Kumar Poonia

14. 0
n0

s ( n)  
c  s(n  1) n  0

So far for n >= k we have


s(n) = ck + s(n-k)
What if k = n?

s(n) = cn + s(0) = cn
Sandeep Kumar Poonia

15. 0
n0

s ( n)  
c  s(n  1) n  0

So far for n >= k we have


s(n) = ck + s(n-k)
What if k = n?

s(n) = cn + s(0) = cn
0
n0

s ( n)  
c  s(n  1) n  0

So

Thus in general

s(n) = cn
Sandeep Kumar Poonia

16. 0
n0

s ( n)  
n  s(n  1) n  0

=
=
=
=
=
=
s(n)
n + s(n-1)
n + n-1 + s(n-2)
n + n-1 + n-2 + s(n-3)
n + n-1 + n-2 + n-3 + s(n-4)
…
n + n-1 + n-2 + n-3 + … + n-(k-1) + s(n-k)
Sandeep Kumar Poonia

17. 0
n0

s ( n)  
n  s(n  1) n  0

=
=
=
=
=
=
s(n)
n + s(n-1)
n + n-1 + s(n-2)
n + n-1 + n-2 + s(n-3)
n + n-1 + n-2 + n-3 + s(n-4)
…
n + n-1 + n-2 + n-3 + … + n-(k-1) + s(n-k)
n
=
i
i  n  k 1
Sandeep Kumar Poonia
 s(n  k )

18. 0
n0

s ( n)  
n  s(n  1) n  0

So far for n >= k we have
n
i
i  n  k 1
Sandeep Kumar Poonia
 s(n  k )

19. 0
n0

s ( n)  
n  s(n  1) n  0

So far for n >= k we have
n
i
 s(n  k )
i  n  k 1

What if k = n?
Sandeep Kumar Poonia

20. 0
n0

s ( n)  
n  s(n  1) n  0

So far for n >= k we have
n
i
 s(n  k )
i  n  k 1

What if k = n?
n 1
 i  s(0)   i  0  n 2
i 1
i 1
n
Sandeep Kumar Poonia
n

21. 0
n0

s ( n)  
n  s(n  1) n  0

So far for n >= k we have
n
i
 s(n  k )
i  n  k 1

What if k = n?
n 1
 i  s(0)   i  0  n 2
i 1
i 1
n

Thus in general
n 1
s ( n)  n
2
Sandeep Kumar Poonia
n

22. c
n 1

 n
T (n)  2T
   c n 1
 2


T(n) =
2T(n/2) + c
2(2T(n/2/2) + c) + c
22T(n/22) + 2c + c
22(2T(n/22/2) + c) + 3c
23T(n/23) + 4c + 3c
23T(n/23) + 7c
23(2T(n/23/2) + c) + 7c
24T(n/24) + 15c
…
2kT(n/2k) + (2k - 1)c
Sandeep Kumar Poonia

23. c
n 1

 n
T (n)  2T
   c n 1
 2


So far for n > 2k we have


T(n) = 2kT(n/2k) + (2k - 1)c
What if k = lg n?

T(n) = 2lg n T(n/2lg n) + (2lg n - 1)c
= n T(n/n) + (n - 1)c
= n T(1) + (n-1)c
= nc + (n-1)c = (2n - 1)c
Sandeep Kumar Poonia

24. The Master Theorem

Given: a divide and conquer algorithm



An algorithm that divides the problem of size n
into a subproblems, each of size n/b
Let the cost of each stage (i.e., the work to divide
the problem + combine solved subproblems) be
described by the function f(n)
Then, the Master Theorem gives us a
cookbook for the algorithm’s running time:
Sandeep Kumar Poonia

25. The Master Theorem

if T(n) = aT(n/b) + f(n) then


 n logb a




logb a
T (n)   n
log n


 f (n) 





Sandeep Kumar Poonia



f (n)  O n logb a 


  0
logb a
f ( n)   n

 c 1


f (n)   n logb a  AND

af (n / b)  cf (n) for large n








26. Using The Master Method

T(n) = 9T(n/3) + n



a=9, b=3, f(n) = n
nlog a = nlog 9 = (n2)
Since f(n) = O(nlog 9 - ), where =1, case 1 applies:
b
3
3



T (n)   nlogb a when f (n)  O nlogb a 

Thus the solution is T(n) = (n2)
Sandeep Kumar Poonia


27. Sorting Revisited

So far we’ve talked about two algorithms to
sort an array of numbers



What is the advantage of merge sort?
What is the advantage of insertion sort?
Next on the agenda: Heapsort

Combines advantages of both previous algorithms
Sandeep Kumar Poonia

28. Heaps

A heap can be seen as a complete binary tree:
16
14
10
8
2


7
4
9
1
What makes a binary tree complete?
Is the example above complete?
Sandeep Kumar Poonia
3

29. Heaps

A heap can be seen as a complete binary tree:
16
14
10
8
2

7
4
1
9
1
1
3
1
1
The book calls them “nearly complete” binary
trees; can think of unfilled slots as null pointers
Sandeep Kumar Poonia
1

30. Heaps

In practice, heaps are usually implemented as
arrays:
16
14
A = 16 14 10 8
7
9
3
2
4
8
1 =
2
Sandeep Kumar Poonia
10
7
4
1
9
3

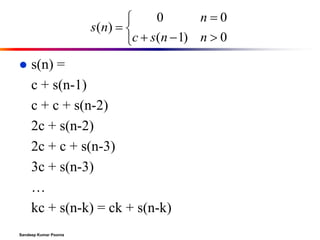
31. Heaps

To represent a complete binary tree as an array:





The root node is A[1]
Node i is A[i]
The parent of node i is A[i/2] (note: integer divide)
The left child of node i is A[2i]
The right child of node i is A[2i + 1]
16
14
A = 16 14 10 8
7
9
3
2
4
8
1 =
2
Sandeep Kumar Poonia
10
7
4
1
9
3

32. Referencing Heap Elements

So…
Parent(i) { return i/2; }
Left(i) { return 2*i; }
right(i) { return 2*i + 1; }
An aside: How would you implement this
most efficiently?
 Another aside: Really?

Sandeep Kumar Poonia

33. The Heap Property

Heaps also satisfy the heap property:
A[Parent(i)]  A[i]
for all nodes i > 1



In other words, the value of a node is at most the
value of its parent
Where is the largest element in a heap stored?
Definitions:


The height of a node in the tree = the number of
edges on the longest downward path to a leaf
The height of a tree = the height of its root
Sandeep Kumar Poonia

34. Heap Height
What is the height of an n-element heap? Why?
 This is nice: basic heap operations take at most
time proportional to the height of the heap

Sandeep Kumar Poonia

35. Heap Operations: Heapify()

Heapify(): maintain the heap property




Given: a node i in the heap with children l and r
Given: two subtrees rooted at l and r, assumed to
be heaps
Problem: The subtree rooted at i may violate the
heap property (How?)
Action: let the value of the parent node “float
down” so subtree at i satisfies the heap property
 What
do you suppose will be the basic operation
between i, l, and r?
Sandeep Kumar Poonia

36. Heap Operations: Heapify()
Heapify(A, i)
{
l = Left(i); r = Right(i);
if (l <= heap_size(A) && A[l] > A[i])
largest = l;
else
largest = i;
if (r <= heap_size(A) && A[r] > A[largest])
largest = r;
if (largest != i)
Swap(A, i, largest);
Heapify(A, largest);
}
Sandeep Kumar Poonia

37. Heapify() Example
16
4
10
14
2
7
8
3
1
A = 16 4 10 14 7
Sandeep Kumar Poonia
9
9
3
2
8
1

38. Heapify() Example
16
4
10
14
2
7
8
3
1
A = 16 4 10 14 7
Sandeep Kumar Poonia
9
9
3
2
8
1

39. Heapify() Example
16
4
10
14
2
7
8
3
1
A = 16 4 10 14 7
Sandeep Kumar Poonia
9
9
3
2
8
1

40. Heapify() Example
16
14
10
4
2
7
8
3
1
A = 16 14 10 4
Sandeep Kumar Poonia
9
7
9
3
2
8
1

41. Heapify() Example
16
14
10
4
2
7
8
3
1
A = 16 14 10 4
Sandeep Kumar Poonia
9
7
9
3
2
8
1

42. Heapify() Example
16
14
10
4
2
7
8
3
1
A = 16 14 10 4
Sandeep Kumar Poonia
9
7
9
3
2
8
1

43. Heapify() Example
16
14
10
8
2
7
4
3
1
A = 16 14 10 8
Sandeep Kumar Poonia
9
7
9
3
2
4
1

44. Heapify() Example
16
14
10
8
2
7
4
3
1
A = 16 14 10 8
Sandeep Kumar Poonia
9
7
9
3
2
4
1

45. Heapify() Example
16
14
10
8
2
7
4
3
1
A = 16 14 10 8
Sandeep Kumar Poonia
9
7
9
3
2
4
1

46. Analyzing Heapify(): Informal
Aside from the recursive call, what is the
running time of Heapify()?
 How many times can Heapify() recursively
call itself?
 What is the worst-case running time of
Heapify() on a heap of size n?

Sandeep Kumar Poonia

47. Analyzing Heapify(): Formal
Fixing up relationships between i, l, and r
takes (1) time
 If the heap at i has n elements, how many
elements can the subtrees at l or r have?


Draw it
Answer: 2n/3 (worst case: bottom row 1/2 full)
 So time taken by Heapify() is given by

T(n)  T(2n/3) + (1)
Sandeep Kumar Poonia

48. Analyzing Heapify(): Formal
So we have
T(n)  T(2n/3) + (1)
 By case 2 of the Master Theorem,
T(n) = O(lg n)
 Thus, Heapify() takes linear time

Sandeep Kumar Poonia

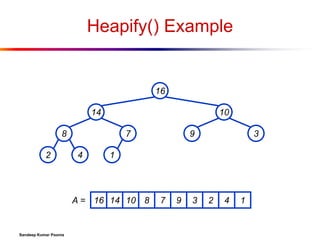
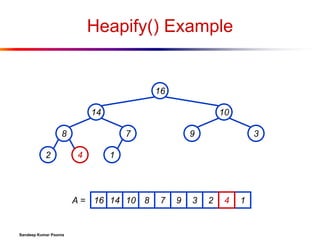
49. Heap Operations: BuildHeap()

We can build a heap in a bottom-up manner by
running Heapify() on successive subarrays


Fact: for array of length n, all elements in range
A[n/2 + 1 .. n] are heaps (Why?)
So:
 Walk
backwards through the array from n/2 to 1, calling
Heapify() on each node.
 Order
of processing guarantees that the children of node
i are heaps when i is processed
Sandeep Kumar Poonia

50. BuildHeap()
// given an unsorted array A, make A a heap
BuildHeap(A)
{
heap_size(A) = length(A);
for (i = length[A]/2 downto 1)
Heapify(A, i);
}
Sandeep Kumar Poonia

51. BuildHeap() Example

Work through example
A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}
4
1
3
2
14
Sandeep Kumar Poonia
16
8
7
9
10

52. Analyzing BuildHeap()

Each call to Heapify() takes O(lg n) time
There are O(n) such calls (specifically, n/2)
 Thus the running time is O(n lg n)




Is this a correct asymptotic upper bound?
Is this an asymptotically tight bound?
A tighter bound is O(n)

How can this be? Is there a flaw in the above
reasoning?
Sandeep Kumar Poonia

53. Analyzing BuildHeap(): Tight

To Heapify() a subtree takes O(h) time
where h is the height of the subtree


h = O(lg m), m = # nodes in subtree
The height of most subtrees is small
Fact: an n-element heap has at most n/2h+1
nodes of height h
 CLR 7.3 uses this fact to prove that
BuildHeap() takes O(n) time

Sandeep Kumar Poonia

54. Heapsort

Given BuildHeap(), an in-place sorting
algorithm is easily constructed:


Maximum element is at A[1]
Discard by swapping with element at A[n]
 Decrement
heap_size[A]
 A[n] now contains correct value

Restore heap property at A[1] by calling
Heapify()

Repeat, always swapping A[1] for A[heap_size(A)]
Sandeep Kumar Poonia

55. Heapsort
Heapsort(A)
{
BuildHeap(A);
for (i = length(A) downto 2)
{
Swap(A[1], A[i]);
heap_size(A) -= 1;
Heapify(A, 1);
}
}
Sandeep Kumar Poonia

56. Analyzing Heapsort
The call to BuildHeap() takes O(n) time
 Each of the n - 1 calls to Heapify() takes
O(lg n) time
 Thus the total time taken by HeapSort()
= O(n) + (n - 1) O(lg n)
= O(n) + O(n lg n)
= O(n lg n)

Sandeep Kumar Poonia

57. Priority Queues
Heapsort is a nice algorithm, but in practice
Quicksort (coming up) usually wins
 But the heap data structure is incredibly useful
for implementing priority queues




A data structure for maintaining a set S of
elements, each with an associated value or key
Supports the operations Insert(),
Maximum(), and ExtractMax()
What might a priority queue be useful for?
Sandeep Kumar Poonia

58. Priority Queue Operations
Insert(S, x) inserts the element x into set S
 Maximum(S) returns the element of S with
the maximum key
 ExtractMax(S) removes and returns the
element of S with the maximum key
 How could we implement these operations
using a heap?

Sandeep Kumar Poonia

59. Tying It Into The Real World

And now, a real-world example…
Sandeep Kumar Poonia

60. Tying It Into The “Real World”

And now, a real-world example…combat billiards






Sort of like pool...
Except you’re trying to
kill the other players…
And the table is the size
of a polo field…
And the balls are the
size of Suburbans...
And instead of a cue
you drive a vehicle
with a ram on it
Figure 1: boring traditional pool
Problem: how do you simulate the physics?
Sandeep Kumar Poonia

61. Combat Billiards:
Simulating The Physics

Simplifying assumptions:

G-rated version: No players
 Just

n balls bouncing around
No spin, no friction
 Easy
to calculate the positions of the balls at time Tn
from time Tn-1 if there are no collisions in between

Simple elastic collisions
Sandeep Kumar Poonia

62. Simulating The Physics

Assume we know how to compute when two
moving spheres will intersect


Given the state of the system, we can calculate
when the next collision will occur for each ball
At each collision Ci:
 Advance
the system to the time Ti of the collision
 Recompute the next collision for the ball(s) involved
 Find the next overall collision Ci+1 and repeat

How should we keep track of all these collisions
and when they occur?
Sandeep Kumar Poonia

63. Implementing Priority Queues
HeapInsert(A, key)
// what’s running time?
{
heap_size[A] ++;
i = heap_size[A];
while (i > 1 AND A[Parent(i)] < key)
{
A[i] = A[Parent(i)];
i = Parent(i);
}
A[i] = key;
}
Sandeep Kumar Poonia

64. Implementing Priority Queues
HeapMaximum(A)
{
// This one is really tricky:
return A[i];
}
Sandeep Kumar Poonia

65. Implementing Priority Queues
HeapExtractMax(A)
{
if (heap_size[A] < 1) { error; }
max = A[1];
A[1] = A[heap_size[A]]
heap_size[A] --;
Heapify(A, 1);
return max;
}
Sandeep Kumar Poonia

66. Back To Combat Billiards





Extract the next collision Ci from the queue
Advance the system to the time Ti of the collision
Recompute the next collision(s) for the ball(s)
involved
Insert collision(s) into the queue, using the time of
occurrence as the key
Find the next overall collision Ci+1 and repeat
Sandeep Kumar Poonia

67. Using A Priority Queue
For Event Simulation
More natural to use Minimum() and
ExtractMin()
 What if a player hits a ball?



Need to code up a Delete() operation
How? What will the running time be?
Sandeep Kumar Poonia

68. Quicksort
Sorts in place
 Sorts O(n lg n) in the average case
 Sorts O(n2) in the worst case
 So why would people use it instead of merge
sort?

Sandeep Kumar Poonia

69. Quicksort

Another divide-and-conquer algorithm

The array A[p..r] is partitioned into two nonempty subarrays A[p..q] and A[q+1..r]
 Invariant:
All elements in A[p..q] are less than all
elements in A[q+1..r]


The subarrays are recursively sorted by calls to
quicksort
Unlike merge sort, no combining step: two
subarrays form an already-sorted array
Sandeep Kumar Poonia

70. Quicksort Code
Quicksort(A, p, r)
{
if (p < r)
{
q = Partition(A, p, r);
Quicksort(A, p, q);
Quicksort(A, q+1, r);
}
}
Sandeep Kumar Poonia

71. Partition

Clearly, all the action takes place in the
partition() function


Rearranges the subarray in place
End result:
 Two
subarrays
 All values in first subarray  all values in second


Returns the index of the “pivot” element
separating the two subarrays
How do you suppose we implement this
function?
Sandeep Kumar Poonia

72. Partition In Words

Partition(A, p, r):


Select an element to act as the “pivot” (which?)
Grow two regions, A[p..i] and A[j..r]
 All
elements in A[p..i] <= pivot
 All elements in A[j..r] >= pivot





Increment i until A[i] >= pivot
Decrement j until A[j] <= pivot
Swap A[i] and A[j]
Repeat until i >= j
Return j
Sandeep Kumar Poonia

73. Partition Code
Partition(A, p, r)
x = A[p];
Illustrate on
i = p - 1;
A = {5, 3, 2, 6, 4, 1, 3, 7};
j = r + 1;
while (TRUE)
repeat
j--;
until A[j] <= x;
What is the running time of
repeat
partition()?
i++;
until A[i] >= x;
if (i < j)
Swap(A, i, j);
else
return j;
Sandeep Kumar Poonia

74. Review: Analyzing Quicksort

What will be the worst case for the algorithm?


What will be the best case for the algorithm?


Partition is balanced
Which is more likely?


Partition is always unbalanced
The latter, by far, except...
Will any particular input elicit the worst case?

Yes: Already-sorted input
Sandeep Kumar Poonia

75. Review: Analyzing Quicksort

In the worst case:
T(1) = (1)
T(n) = T(n - 1) + (n)

Works out to
T(n) = (n2)
Sandeep Kumar Poonia

76. Review: Analyzing Quicksort

In the best case:
T(n) = 2T(n/2) + (n)

What does this work out to?
T(n) = (n lg n)
Sandeep Kumar Poonia

77. Review: Analyzing Quicksort
(Average Case)

Intuitively, a real-life run of quicksort will
produce a mix of “bad” and “good” splits



Randomly distributed among the recursion tree
Pretend for intuition that they alternate between
best-case (n/2 : n/2) and worst-case (n-1 : 1)
What happens if we bad-split root node, then
good-split the resulting size (n-1) node?
Sandeep Kumar Poonia

78. Review: Analyzing Quicksort
(Average Case)

Intuitively, a real-life run of quicksort will
produce a mix of “bad” and “good” splits



Randomly distributed among the recursion tree
Pretend for intuition that they alternate between
best-case (n/2 : n/2) and worst-case (n-1 : 1)
What happens if we bad-split root node, then
good-split the resulting size (n-1) node?
 We
end up with three subarrays, size 1, (n-1)/2, (n-1)/2
 Combined cost of splits = n + n -1 = 2n -1 = O(n)
 No worse than if we had good-split the root node!
Sandeep Kumar Poonia

79. Review: Analyzing Quicksort
(Average Case)
Intuitively, the O(n) cost of a bad split
(or 2 or 3 bad splits) can be absorbed
into the O(n) cost of each good split
 Thus running time of alternating bad and good
splits is still O(n lg n), with slightly higher
constants
 How can we be more rigorous?

Sandeep Kumar Poonia

80. Analyzing Quicksort: Average Case

For simplicity, assume:


All inputs distinct (no repeats)
Slightly different partition() procedure
 partition
around a random element, which is not
included in subarrays
 all splits (0:n-1, 1:n-2, 2:n-3, … , n-1:0) equally likely
What is the probability of a particular split
happening?
 Answer: 1/n

Sandeep Kumar Poonia

81. Analyzing Quicksort: Average Case
So partition generates splits
(0:n-1, 1:n-2, 2:n-3, … , n-2:1, n-1:0)
each with probability 1/n
 If T(n) is the expected running time,

1 n1
T n    T k   T n  1  k   n 
n k 0
What is each term under the summation for?
 What is the (n) term for?

Sandeep Kumar Poonia

82. Analyzing Quicksort: Average Case

So…
1 n 1
T n    T k   T n  1  k   n 
n k 0
2 n 1
  T k   n 
n k 0
Sandeep Kumar Poonia
Write it on
the board

83. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method




Guess the answer
Assume that the inductive hypothesis holds
Substitute it in for some value < n
Prove that it follows for n
Sandeep Kumar Poonia

84. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 What’s



the answer?
Assume that the inductive hypothesis holds
Substitute it in for some value < n
Prove that it follows for n
Sandeep Kumar Poonia

85. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)



= O(n lg n)
Assume that the inductive hypothesis holds
Substitute it in for some value < n
Prove that it follows for n
Sandeep Kumar Poonia

86. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)

= O(n lg n)
Assume that the inductive hypothesis holds
 What’s


the inductive hypothesis?
Substitute it in for some value < n
Prove that it follows for n
Sandeep Kumar Poonia

87. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)

Assume that the inductive hypothesis holds
 T(n)


= O(n lg n)
 an lg n + b for some constants a and b
Substitute it in for some value < n
Prove that it follows for n
Sandeep Kumar Poonia

88. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)

Assume that the inductive hypothesis holds
 T(n)

= O(n lg n)
 an lg n + b for some constants a and b
Substitute it in for some value < n
 What

value?
Prove that it follows for n
Sandeep Kumar Poonia

89. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)

Assume that the inductive hypothesis holds
 T(n)

 an lg n + b for some constants a and b
Substitute it in for some value < n
 The

= O(n lg n)
value k in the recurrence
Prove that it follows for n
Sandeep Kumar Poonia

90. Analyzing Quicksort: Average Case

We can solve this recurrence using the dreaded
substitution method

Guess the answer
 T(n)

Assume that the inductive hypothesis holds
 T(n)

 an lg n + b for some constants a and b
Substitute it in for some value < n
 The

= O(n lg n)
value k in the recurrence
Prove that it follows for n
 Grind
Sandeep Kumar Poonia
through it…

91. Analyzing Quicksort: Average Case
2 n 1
T n    T k   n 
n k 0
2 n 1
  ak lg k  b   n 
n k 0
The recurrence to be solved
Plug in inductive hypothesis
What are we doing here?
2  n 1

What are we doing here?
 b   ak lg k  b   n  Expand out the k=0 case
n  k 1

2 n 1
2b
  ak lg k  b  
 n 
n k 1
n
2b/n is just a constant,
What are we doing here?
so fold it into (n)
2 n 1
  ak lg k  b   n 
n k 1
Note: leaving the same
recurrence as the book
Sandeep Kumar Poonia

92. Analyzing Quicksort: Average Case
2 n 1
T n    ak lg k  b   n 
n k 1
2 n 1
2 n 1
  ak lg k   b  n 
n k 1
n k 1
The recurrence to be solved
Distribute the summation
What are we doing here?
2a n 1
2b
the summation:

k lg k  (n  1)  n  Evaluateare we doing here?
What

b+b+…+b = b (n-1)
n k 1
n
2a n 1

 k lg k  2b  n 
n k 1
This summation gets its own set of slides later
Sandeep Kumar Poonia
Since n-1<n,we doing here?
What are 2b(n-1)/n < 2b

93. Analyzing Quicksort: Average Case
2a n 1
T n  
 k lg k  2b  n 
n k 1




The recurrence to be solved
2a  1 2
1 2
We’ll prove this
 n lg n  n   2b  n  What the hell? later
n 2
8 
a
an lg n  n  2b  n 
Distribute the (2a/n) term
What are we doing here?
4
a  Remember, our goal is to get

an lg n  b   n   b  n 
What are we doing here?
T(n)  an lg n + b
4 

Pick a large enough that
an lg n  b
How did we do this?
an/4 dominates (n)+b
Sandeep Kumar Poonia

94. Analyzing Quicksort: Average Case

So T(n)  an lg n + b for certain a and b




Thus the induction holds
Thus T(n) = O(n lg n)
Thus quicksort runs in O(n lg n) time on average
(phew!)
Oh yeah, the summation…
Sandeep Kumar Poonia

95. Tightly Bounding
The Key Summation
n 1
n 2 1
n 1
k 1
k 1
k  n 2 
n 2 1
n 1
k 1
k  n 2 
 k lg k   k lg k   k lg k

 k lg k   k lg n
Sandeep Kumar Poonia
n 1
k 1

n 2 1
k  n 2 
 k lg k  lg n  k
Split the summation for a
What are we doing here?
tighter bound
The lg k in the second term
What are we doing here?
is bounded by lg n
Move the lg n outside the
What are we doing here?
summation

96. Tightly Bounding
The Key Summation
n 1
 k lg k 
k 1
n 2 1
 k lg k  lg n
k 1
n 1
k
The summation bound so far
k  n 2 

n 1
k 1

n 2 1
k  n 2 
 k lgn 2  lg n  k
n 2 1
 k lg n  1  lg n
k 1
n 1
k
n 1
k 1
Sandeep Kumar Poonia
lg n/2 = lg n we doing here?
What are - 1
k  n 2 
n 2 1
k  n 2 
 lg n  1
The lg k in the first term is
What are we doing here?
bounded by lg n/2
 k  lg n  k
Move (lg n - 1) outside the
What are we doing here?
summation

97. Tightly Bounding
The Key Summation
n 2 1
n 1
 k lg k  lg n  1
k 1
 lg n
 k  lg n
k 1
n 2 1
k 
k 1
k
 k  lg n
k 1
n 1
k
Distribute the (lg n - 1)
What are we doing here?
k  n 2 
n 2 1
k 1
The summation bound so far
k  n 2 
n 2 1
n 1
k 1
 lg n k 
k
 n  1(n) 
 lg n

2


Sandeep Kumar Poonia
n 1
The summations overlap in
What are we doing here?
range; combine them
n 2 1
k
k 1
The Guassian series here?
What are we doing

98. Tightly Bounding
The Key Summation
 n  1(n) 
 k lg k   2  lg n   k


k 1
k 1
n 2 1
1
 nn  1lg n   k
2
k 1
n 2 1
n 1
The summation bound so far
Rearrange first term, place
What are we doing here?
upper bound on second
1
1  n  n 
 nn  1lg n     1
2
2  2  2 
1 2
1 2 n
 n lg n  n lg n  n 
2
8
4

Sandeep Kumar Poonia

X Guassian series
What are we doing?
Multiply it
What are we doing?
all out

99. Tightly Bounding
The Key Summation

n 1

1 2
1 2 n
 k lg k  2 n lg n  n lg n  8 n  4
k 1
1 2
1 2
 n lg n  n when n  2
2
8
Done!!!
Sandeep Kumar Poonia