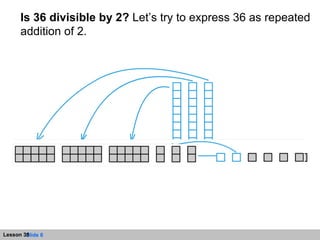
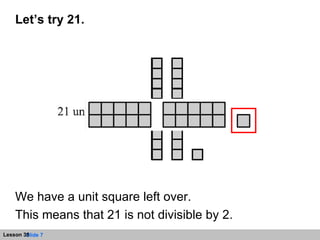
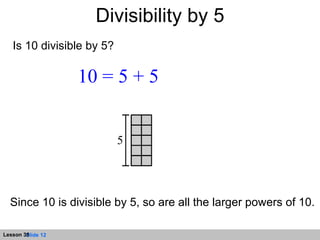
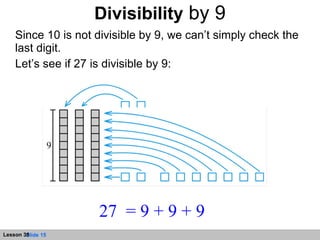
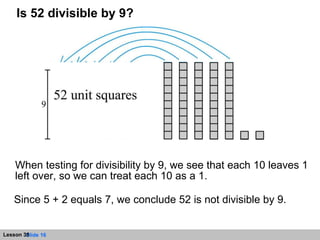
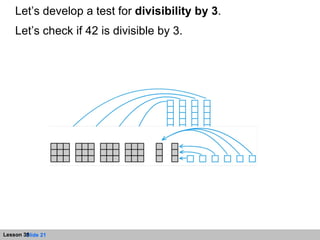
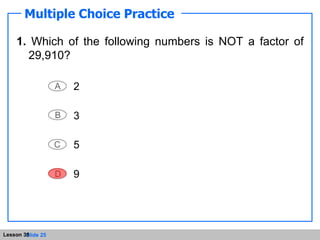
The document discusses divisibility rules for determining if a number is divisible by 2, 3, 5, or 9. It provides explanations and examples of applying the rules. The rules are: - Divisible by 2 if the number ends in 0, 2, 4, 6, or 8 - Divisible by 5 if the number ends in 0 or 5 - Divisible by 9 if the sum of its digits is divisible by 9 - Divisible by 3 if the sum of its digits is divisible by 3 The document includes examples of applying the rules and checking for understanding questions.

1. Chapter 7 Lesson 35 Testing for Divisibility WO.17 Use long division to determine if one number is divisible by another. WO.23 Use divisibility rules to determine if a number is divisible by 2, 3, 5, or 9 and understand the justification for these rules.

2. Objectives Understand and use the divisibility rules for 2, 3, 5 and 9.

3. Remember from Before What is a factor? What is a multiple? How are multiples and factors related?

4. Get Your Brain in Gear 1. Use mental math to divide 369 by 9. 2. Use mental math to divide 85 by 5. 41 17

5. Multiples of 2 . All multiples of 2 can be expressed as the repeated addition of 2. 10 = 2 + 2 + 2 + 2 + 2

6. Is 36 divisible by 2? Let’s try to express 36 as repeated addition of 2.

7. Let’s try 21. We have a unit square left over. This means that 21 is not divisible by 2.

8. What about larger powers of 10? 100 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 100 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 Since all the powers of ten are multiples of 10, they also are all multiples of 2.

9. Divisible by 2 rule: If a whole number ends in 0, 2, 4, 6 or 8, then the number is divisible by 2. Otherwise it is not divisible by 2.

10. Applying the rule, is the following number divisible by 2? 47,297,59 3 The digit in the 10 0 place is 3, and 3 is not divisible by 2.

11. Check for Understanding 1. Determine whether the number is divisible by 2. a. 23 b. 78 c. 504 d. 8,241 e. 6,794 Not divisible by 2. Divisible by 2. Not divisible by 2. Divisible by 2. Divisible by 2.

12. Divisibility by 5 Is 10 divisible by 5? 10 = 5 + 5 Since 10 is divisible by 5, so are all the larger powers of 10.

13. Divisibility by 5 rule: If a whole number ends in 0 or 5, then the number is divisible by 5. Otherwise it is not divisible by 5. According to this rule, would 36 5 be divisible by 5?

14. Check for Understanding 2. Determine if the number is divisible by 5. a. 70 b. 553 d. 72865 c. 10003 e. 8003000 Divisible by 5. Divisible by 5. Divisible by 5. Not divisible by 5. Not divisible by 5.

15. Divisibility by 9 Since 10 is not divisible by 9, we can’t simply check the last digit. Let’s see if 27 is divisible by 9: 27 = 9 + 9 + 9

16. When testing for divisibility by 9, we see that each 10 leaves 1 left over, so we can treat each 10 as a 1. Is 52 divisible by 9? Since 5 + 2 equals 7, we conclude 52 is not divisible by 9.

17. Is 63 divisible by 9? Remember, each 10 is treated as a 1. Since 6 + 3 equals 9, this means 63 is divisible by 9. Is 85 divisible by 9? How do you know?

18. 7 + 5 + 6 = 18 Since 18 is divisible by 9, we conclude that 756 is also divisible by 9. What about larger numbers? Is 756 divisible by 9?

19. If the digits of a whole number add up to a multiple of 9, then the number is divisible by 9. Otherwise it is not divisible by 9.

20. Check for Understanding 3. Determine whether the number is divisible by 9. a. 73 b. 108 c. 7812 d. 6873 e. 98016 Not divisible by 9. Not divisible by 9. Not divisible by 9. Divisible by 9. Divisible by 9.

21. Let’s develop a test for divisibility by 3 . Let’s check if 42 is divisible by 3.

22. If the digits of a whole number add up to a multiple of 3, then the number is divisible by 3. Otherwise it is not divisible by 3. Is 592 divisible by 3? 5 + 9 + 2 = 16 1 + 6 = 7

23. We can verify that 592 is not divisible by 3 using long division:

24. Check for Understanding 4. Test whether the number is divisible by 3. Verify the result using long division. 5. Using what you learned in this lesson, how can you quickly determine if 1,335 is divisible by 15? Is it? 6. What is the smallest number you can add to 7,120 to make it divisible by 3? 7. When you divide 2,349,684 by 5, will there be a remainder? What will the remainder be? a. 84 b. 275 c. 1086 d. 23938 e. 62505 Yes Yes Yes No No You check to see if it is divisible by 3 and divisible by 5. Thus 1,335 is divisible by 15. Add 2. 7,122 is divisible by 3. Yes; 4

25. Multiple Choice Practice 1. Which of the following numbers is NOT a factor of 29,910? 2 3 5 9

26. A student made the following claims about divisibility. What is the student misunderstanding? What would you tell this student to correct their understanding? Find the Errors The student was able to correctly determine if a number is divisible by 2 or 5, but misunderstood how to test for divisibility of 3. You cannot in general look at the last digit to determine if it is divisible by 3, you must add all the digits together and check if the number is a multiple of 3. 5 + 2 + 3 = 10, which is not a multiple of 3. Therefore, 523 is not divisible by 3.