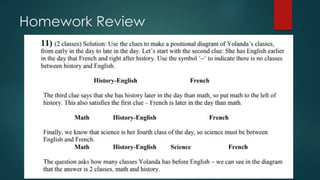
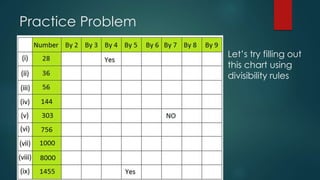
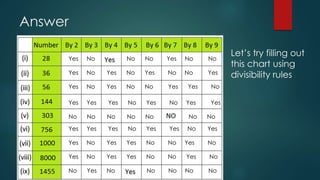
The document provides an overview of divisibility, defining it as a number's ability to be evenly divided by another number without a remainder. It outlines specific rules for determining divisibility by numbers 2 through 10, including examples and practice problems. The content emphasizes the practical utility of these rules for simplifying division, particularly for larger numbers.