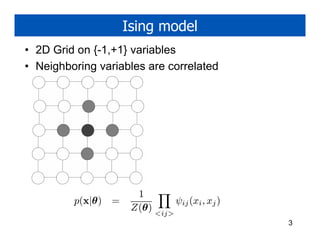
1. Gibbs sampling is a technique for drawing samples from probability distributions by iteratively sampling each variable conditioned on the current values of the other variables. It can be used to sample from Markov random fields and Bayesian networks. 2. An Ising model is a Markov random field with binary variables on a grid that are correlated with their neighbors. Gibbs sampling in an Ising model samples each variable based on its neighbors' current values. 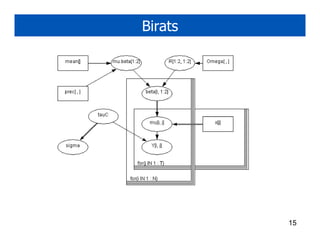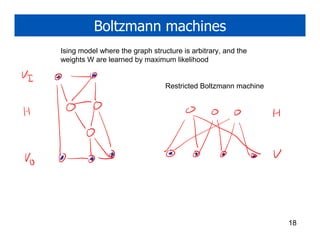3. Boltzmann machines generalize the Ising model to arbitrary graph structures between variables. Restricted Boltzmann machines and Hopfield networks are specific types of Boltzmann machines.

1. CS340 Machine learning
Gibbs sampling in Markov random fields
1

2. Image denoising
x y
ˆ
x = E[x|y, θ]
2

3. Ising model
• 2D Grid on {-1,+1} variables
• Neighboring variables are correlated
1
p(x|θ) = ψij (xi , xj )
Z(θ) <ij>
3

4. Ising model
eW e−W
ψij (xi , xj ) =
e−W eW
W > 0: ferro magnet
W < 0: anti ferro magnet (frustrated system)
1
p(x|θ) = exp[−βH(x|θ)]
Z(θ)
H(x) = −xT Wx = − Wij xi xj
<ij>
β=1/T = inverse temperature
4

5. Samples from an Ising model
W=1
Cold T=2 Hot T=5
Mackay fig 31.2 5

6. Boltzmann distribution
• Prob distribution in terms of clique potentials
1
p(x|θ) = ψc (xc |θ c )
Z(θ)
c∈C
• In terms of energy functions
ψc (xc ) = exp[−Hc (xc )]
log p(x) = −[ Hc (xc ) + log Z]
c∈C
6

7. Ising model
• 2D Grid on {-1,+1} variables
• Neighboring variables are correlated
Wij −Wij
Hij =
−Wij Wij
W > 0: ferro magnet
W < 0: anti ferro magnet (frustrated)
H(x) = −xT Wx = − Wij xi xj
<ij>
1
p(x|θ ) = exp[−βH(x|θ )]
Z(θ )
β=1/T = inverse temperature 7

8. Local evidence
 
1
p(x, y) = p(x)p(y|x) =  ψij (xi , xj ) p(yi |xi )
Z <ij> i
p(yi |xi ) = N (yi |xi , σ 2 )
8

9. Gibbs sampling
• A way to draw samples from p(x1:d|y,θ) one variable
at a time, ie. p(xi|x-i)
1. xs+1 ∼ p(x1 |xs , . . . , xs )
1 2 D
2. xs+1 ∼ p(x2 |xs+1 , xs , . . . , xs )
2 1 3 D
3. xs+1 ∼ p(xi |xs+1 , xs
i 1:i−1 i+1:D )
4. xs+1 ∼ p(xD |xs+1 , . . . , xs+1 )
D 1 D−1
9

10. Gibbs sampling from a 2d Gaussian
Mackay 29.13 10

11. Gibbs sampling in an MRF
• Full conditional depends only on Markov blanket
p(xi = ℓ, x−i )
p(Xi = ℓ|x−i ) = ′
ℓ′ p(Xi = ℓ , x−i )
(1/Z)[ j∈Ni ψij (Xi = ℓ, xj )][ <jk>:j,k∈Fi ψjk (xj , xk )]
=
(1/Z) ℓ′ [ j∈Ni ψij (Xi = ℓ′ , xj )][ <j,k>:j,k∈Fi ψjk (xj , xk )]
j∈Ni ψij (Xi = ℓ, xj )
=
ℓ′ j∈Ni ψij (Xi = ℓ′ , xj )
11

12. Gibbs sampling in an Ising model
• Let ψ(xi,xj) = exp(W xi xj), xi = +1,-1.
j∈Ni ψij (Xi = +1, xj )
p(Xi = +1|x−i ) =
j∈Ni ψij (Xi = +1, xj ) + j∈Ni ψij (Xi = −1, xj )
exp[J j∈Ni xj ]
=
exp[J j∈Ni xj ] + exp[−J j∈Ni xj ]
exp[Jwi ]
=
exp[Jwi ] + exp[−Jwi ]
= σ(2J wi )
wi = xj
j∈Ni
σ(u) = 1/(1 + e−u )
12

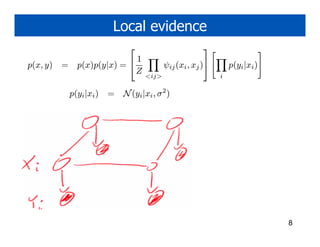
13. Adding in local evidence
• Final form is
exp[J wi ]φi (+1, yi )
p(Xi = +1|x−i , y) =
exp[Jwi ]φi (+1, yi ) + exp[−Jwi ]φi (−1, yi )
Run demo
13

14. Gibbs sampling for DAGs
• The Markov blanket of a node is the set that
renders it independent of the rest of the graph.
• This is the parents, children and co-parents.
p(Xi , X−i )
p(Xi |X−i ) =
x p(Xi , X−i )
p(Xi , U1:n , Y1:m , Z1:m , R)
=
x p(x, U1:n , Y1:m , Z1:m , R)
p(Xi |U1:n )[ j p(Yj |Xi , Zj )]P (U1:n , Z1:m , R)
=
x p(Xi = x|U1:n )[ j p(Yj |Xi = x, Zj )]P (U1:n , Z1:m , R)
p(Xi |U1:n )[ j p(Yj |Xi , Zj )]
=
x p(Xi = x|U1:n )[ j p(Yj |Xi = x, Zj )]
p(Xi |X−i ) ∝ p(Xi |P a(Xi )) p(Yj |P a(Yj )
Yj ∈ch(Xi )
14

15. Birats
15

16. Samples
16

17. Posterior predictive check
17

18. Boltzmann machines
Ising model where the graph structure is arbitrary, and the
weights W are learned by maximum likelihood
Restricted Boltzmann machine
18

19. Hopfield network
Boltzmann machine with no hidden nodes (fully connected Ising model)
19