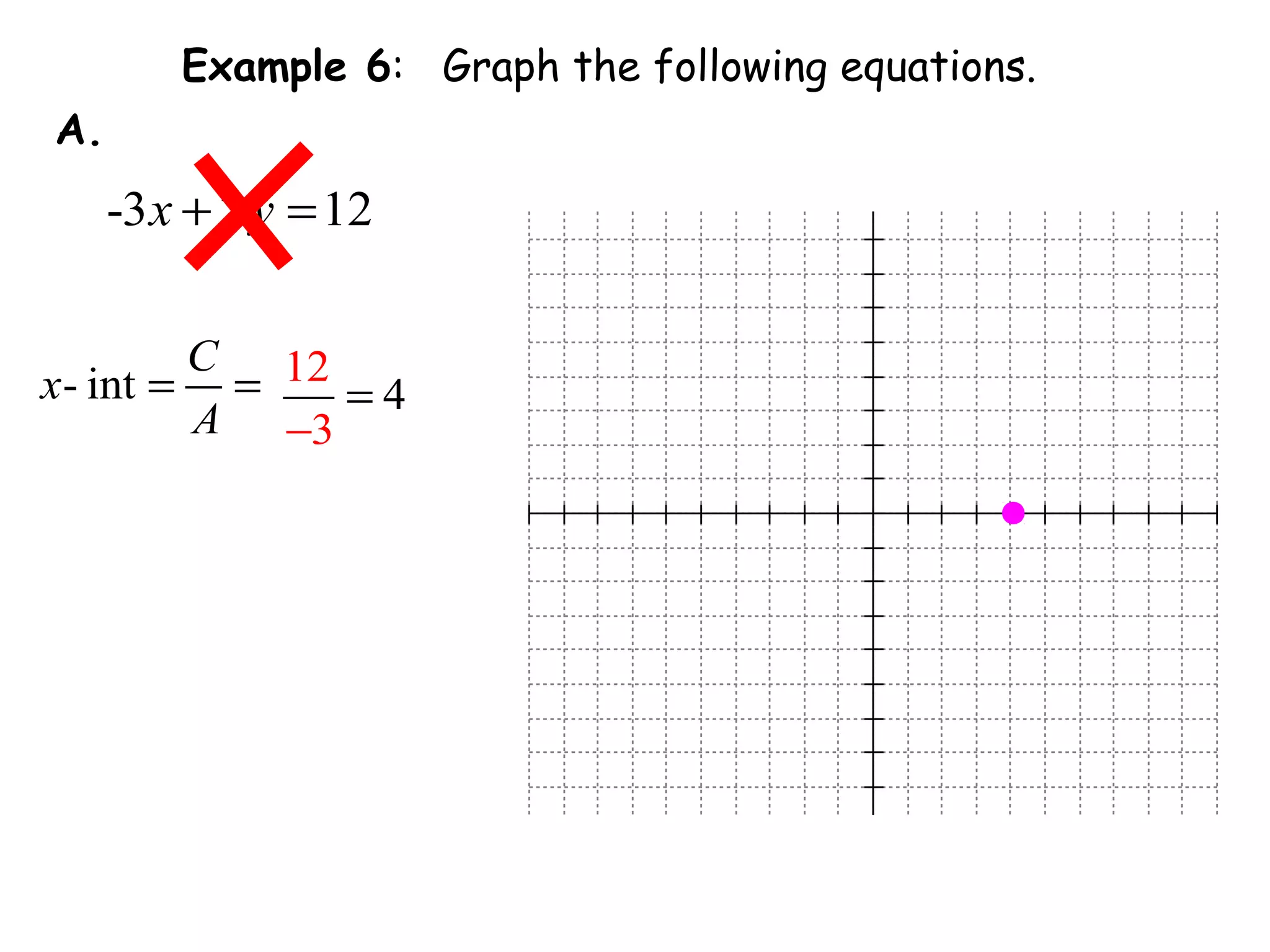
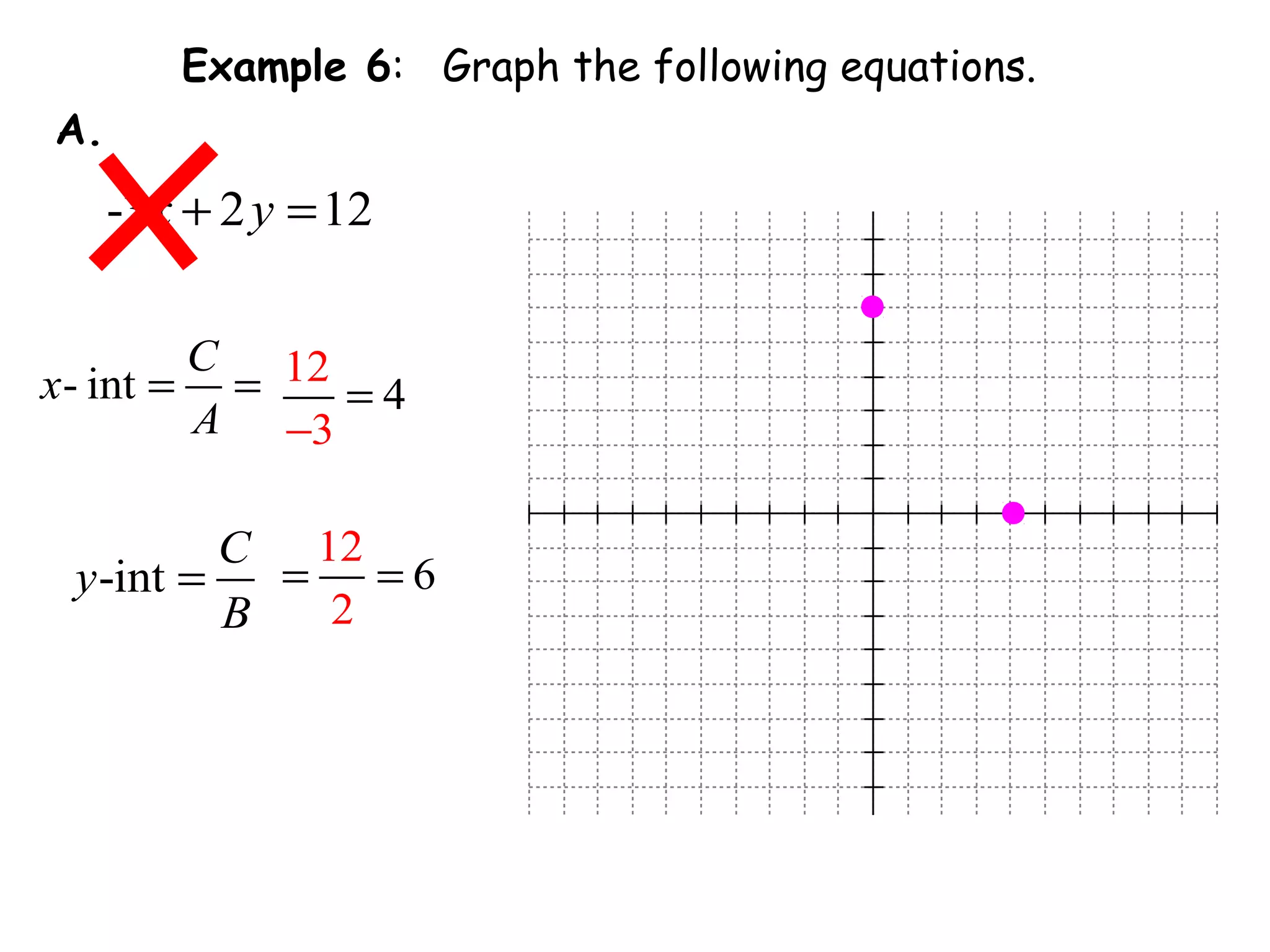
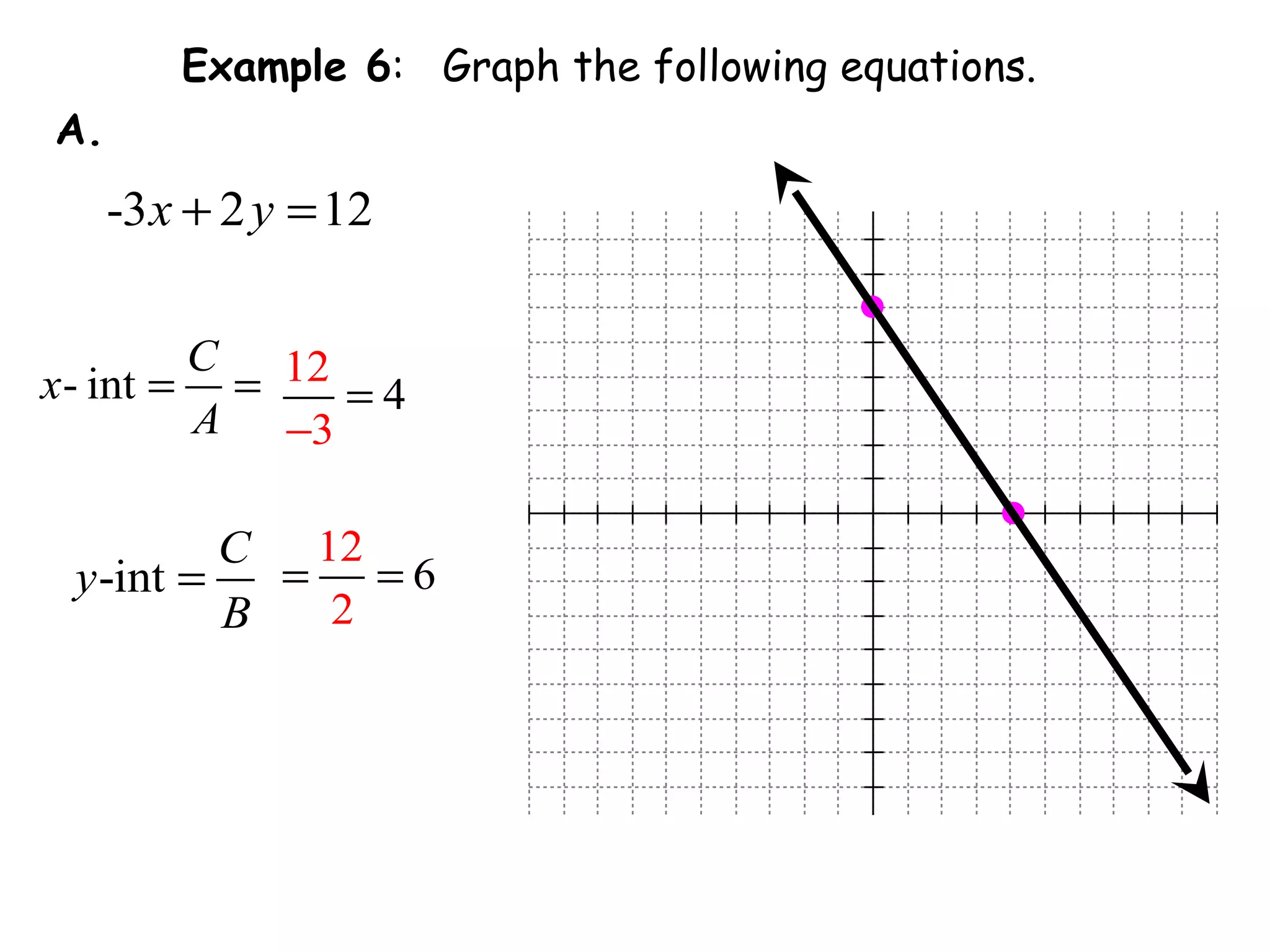
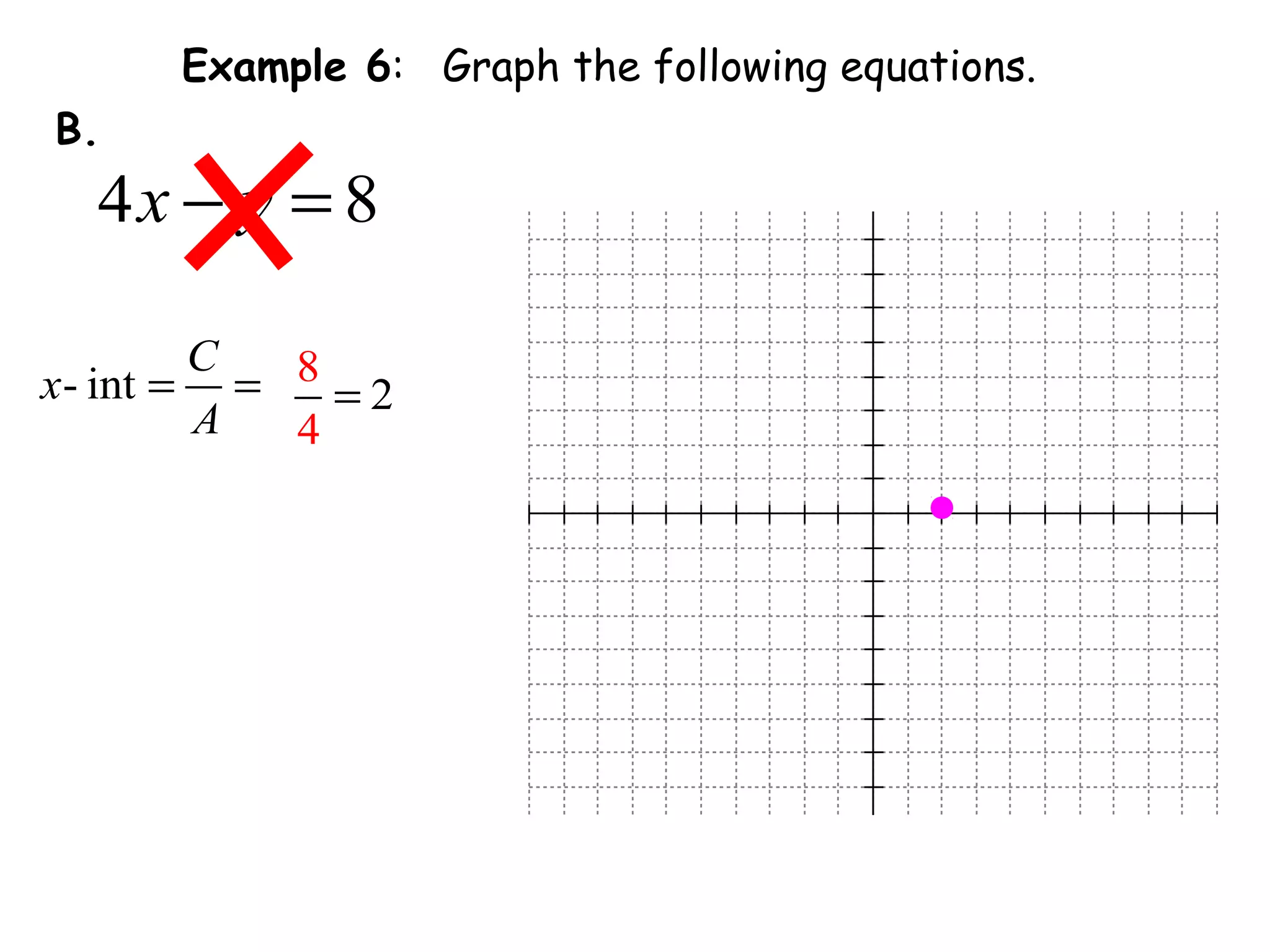
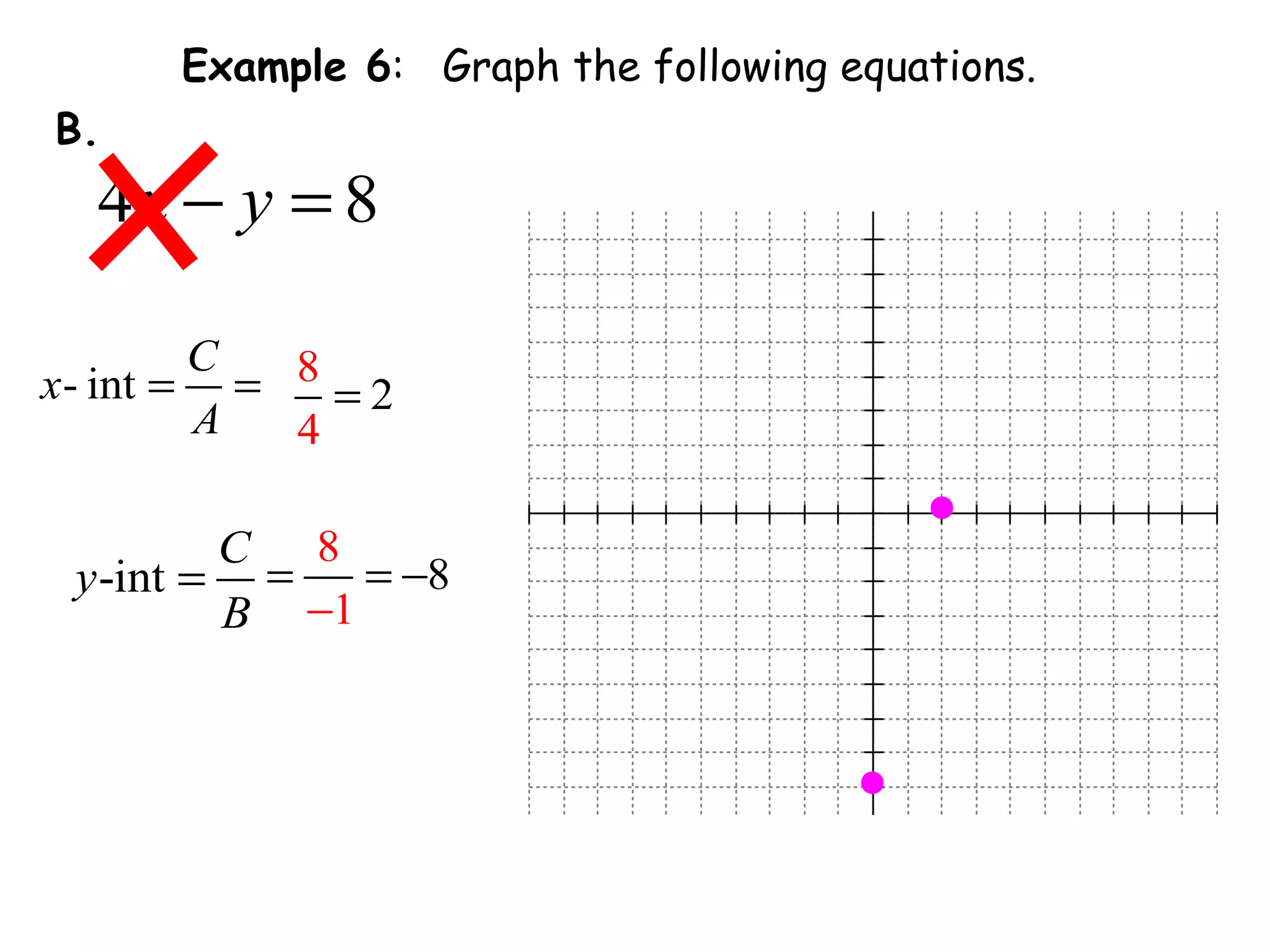
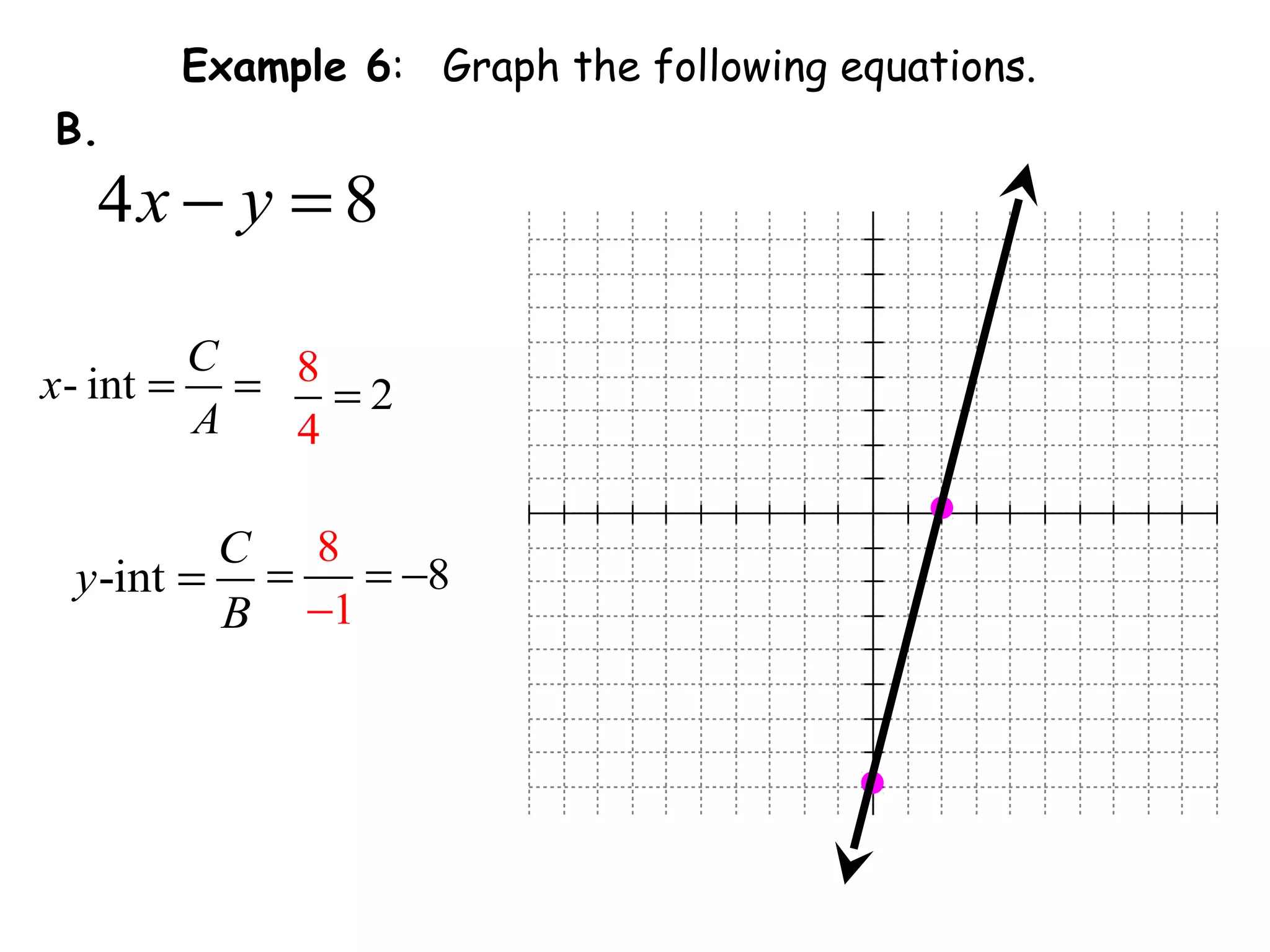
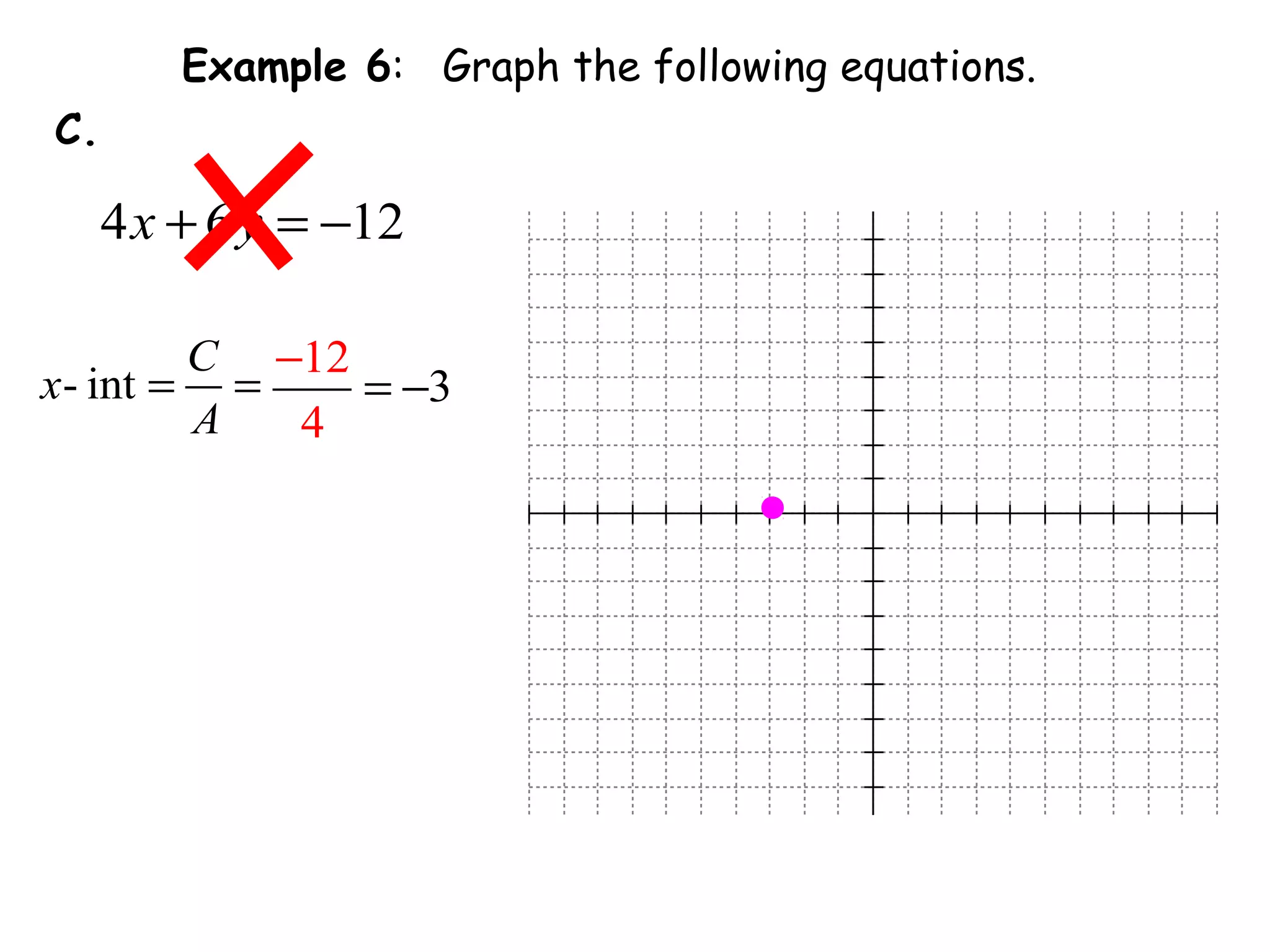
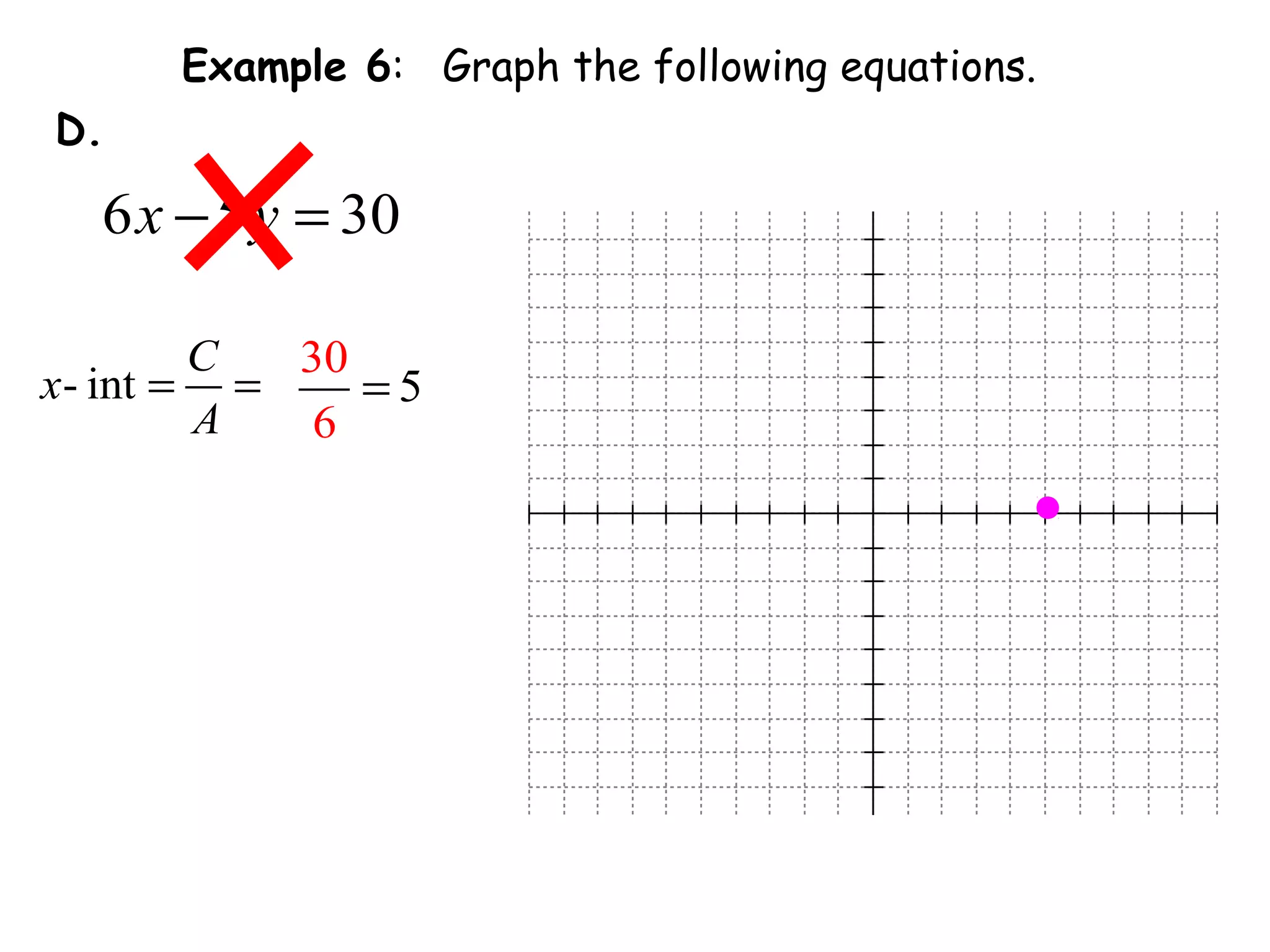
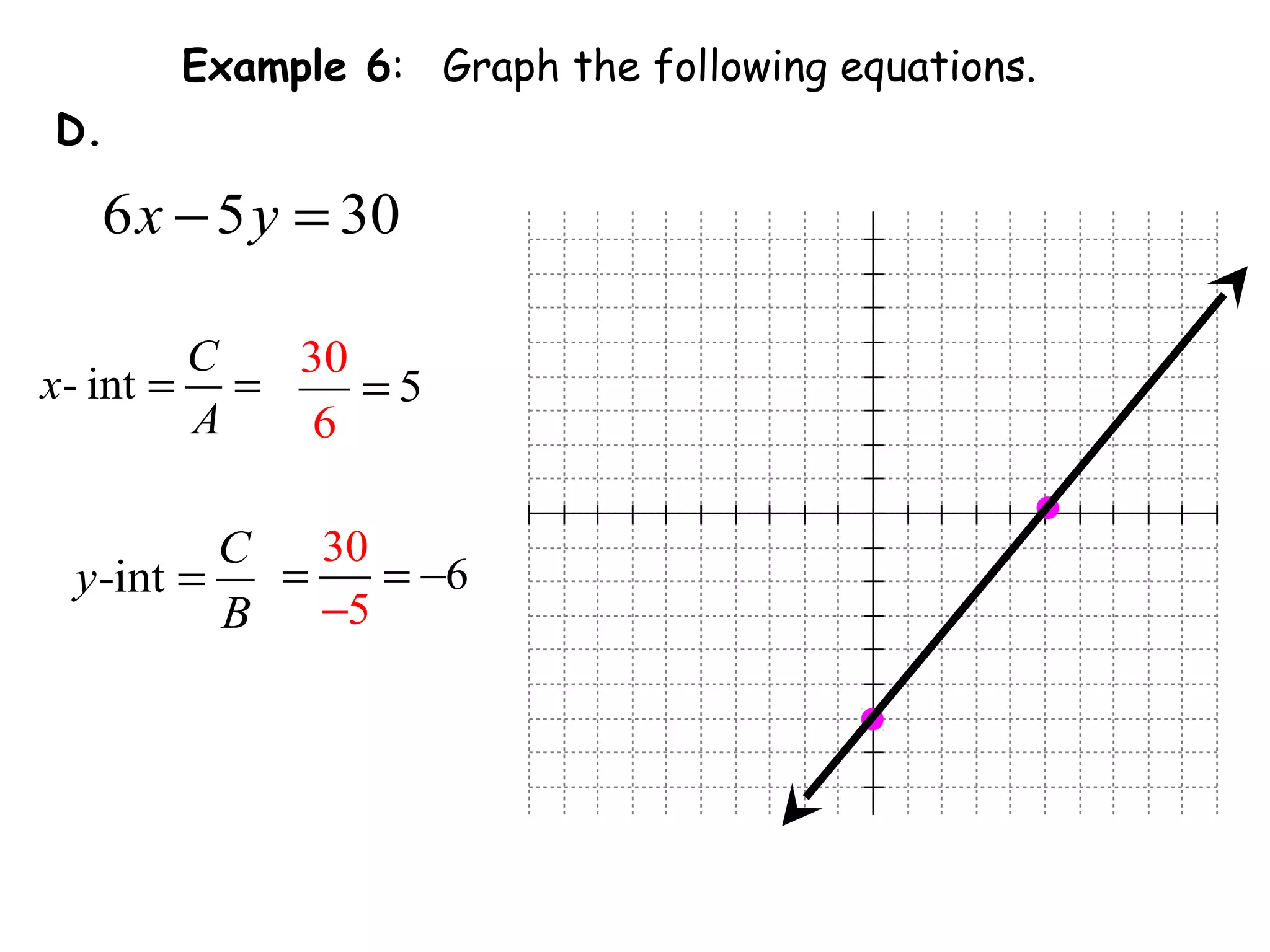
This document discusses linear equations in standard form. It begins by defining standard form as Ax + By = C, where A, B, and C are integers. It provides examples of writing equations in standard form and moving terms to standard form. The document also discusses finding the x-intercept, y-intercept, and slope of equations written in standard form. It provides examples of using the intercepts to graph linear equations written in standard form.

1. FORMS OF A
LINEAR EQUATION

2. OBJECTIVE

3. Activity:
1. Close your eyes and imagine
yourself 10 years from now
applying for a job.
2. The company you are applying
for set a standard that all
applicants who meet the
standards will be hired.

4. How will you set yourself in order to
meet the standard of the company?
Explain

5. Do you think you will be accepted as
an employee? Why? How?

6. What is Standard? How will you
relate this in the standard form in
linear equations.

7. The equation 2 3y x= − +
is written _______________ form.
If we move “ 2x−
we have _______________________.
” to the other side of the equation,
2 3y x= − +
slope intercept
2x+
2 3x y+ =
2 3x y+ =

8. If we move “ 2x−
we have _______________________.
” to the other side of the equation,
2 3x y+ =
This is still a ________ equation, but it is written
in a different form.
linear
A linear equation in the form _______________
is in ______________, where A, B, and C are
integers.
Ax By C+ =
standard form

9. A linear equation in the form _______________
is in ______________, where A, B, and C are
integers.
Ax By C+ =
standard form
Remember the set of integers is
 
 
 
.
... 4, 3, 2, 1, 0,1, 2, 3, 4...− − − −
NO FRACTIONS!!!
NO DECIMALS !!!

10. Example 1:
A. Jackie is in charge of selling tickets for the ONHS Rondalla
concert at Php2.00 for students and Php4.00 for adults. She
hopes that the total ticket sales will be about Php600 in order to
cover expenses and make a modest profit.
Write a linear equation in standard form to model this
situation.
Let x =
y =
# student tickets
# adult tickets
Php2.00
Php4.00
2.00 4.00 600x y+ =
2 4 600x y+ =

11. B. A donation of Php300 was make to the Waray Waray Music Club
for the purpose of building their collection of CDs. At the local
music store, some waray waray CDs cost Php10 and other cost
Php15. The club wants to know how many of each type can buy
with the Php300.
(Do not consider sales tax.)
Write an equation in standard form to model this
situation.
Let x =
y =
# waray waray CDs
# other CDs
Php10.00
Php15.00
10.00 15.00 300x y+ =
10 15 300x y+ =

12. 5 2 4y x− =
x-term + y-term = constant
No fractions, no decimals !4 2 2x y+ = −
5
8
7
y x= − +
2
5
3
x y+ = −
7 3 5x y− + = −
7.5 4.3x y+ =
A
B
C
D
E
F
Example 2: Tell whether the equations below are in standard form.
NO
YES
NO
NO
YES
NO
FRACTIONS
DECIMALS

13. If an equation is not written in standard form, we can
rewrite the equation so that it is in standard form.
Example 3: Write each linear equation in standard form.
A. 57 2 4y x− = B. 3
8
7
y x= − +2y+
57 4 2x y= +
4 2 57x y+ =
7 7 7
7 3 56y x= − +
3x+
3 7 56x y+ =
3 7 56x y+ =4 2 57x y+ =

14. C.
57 2 4y x− =D.
53+
57 40 53x y+ =
57 4 2x y= +
2y+
4 2 57x y+ =
4 2 57x y+ =
57 40 53x y+ =
5.7 5.3 4x y− =
10 10 10
57 53 40x y− =
40y+

15. We can find the ___& ___ intercepts and the ________
when the equation is written in standard form.
x y slope
x-intercept is at
y =
y-intercept is at
x =
( 2,0)−
0
(0,3)
0

16. x-intercept is
at
y =
y-intercept is
at
x =
( 2,0)−
0
(0,3)
0
We know that y = 0 at the ____ intercept,
so we can plug in 0 for ___ to find the _____ intercept.
We know that x = 0 at the ____ intercept,
so we can plug in 0 for ___ to find the _____ intercept.
x
y x
y
yx

17. Example 4: Find the x & y intercepts of the following equations.
A. 4 2 12x y+ = −
x- intercept y-intercept
Plug in 0
for y
Plug in 0
for x
( )04 2 12x + = −
4 12x = −
4 4
3x = −
( )intercept 3,0x → −
( )4 10 2 2y+ = −
2 12y = −
2 2
6y = −
( )intercept 0, 6y → −

18. Example 4: Find the x & y intercepts of the following equations.
B.
x- intercept y-intercept
Plug in 0
for y
Plug in 0
for x
( )2 3 180x − =
2 18x =
2 2
9x =
( )intercept 9,0x →
( )2 3 10 8y− =
3 18y− =
3 3− −
6y = −
( )intercept 0, 6y → −
2 3 18x y− =

19. Example 4: Find the x & y intercepts of the following equations.
C.
x- intercept y-intercept
Plug in 0
for y
Plug in 0
for x
( )0Ax B C+ =
Ax C=
A A
C
x
A
=
intercept ,0
C
x
A
 
→ ÷
 
( )0A By C+ =
By C=
B B
C
y
B
=
intercept 0,
C
y
B
 
→ ÷
 
Ax By C+ =

20. x- intercept y-intercept
C
x
A
=
intercept ,0
C
x
A
 
→ ÷
 
C
y
B
=
intercept 0,
C
y
B
 
→ ÷
 
Ax By C+ =
Write in slope-intercept form to find the slope.Ax By C+ =

21. Ax By C+ =
Ax−
By Ax C= − +
B B B
A C
y x
B B
= − +
x- intercept y-intercept
C
x
A
=
intercept ,0
C
x
A
 
→ ÷
 
C
y
B
=
intercept 0,
C
y
B
 
→ ÷
 
Ax By C+ =
A
m
B
= −

22. x - intercept =
y - intercept =Slope =
Ax CBy+ =
B
A−

23. x - intercept =
y - intercept =Slope =
C
A
Ax CBy+ =
To find the x-intercept, cross out the y-term…
B
A−

24. x - intercept =
y - intercept =Slope =
C
A
Ax CBy+ =
B
A−
To find the y-intercept, cross out the x-term…
C
B

25. -3 2 12x y+ =
Example 5: Find the slope and x & y intercepts of the
following equations.
A.
A =
B =
C =
3−
2+
12
Slope x- intercept y-intercept
A
m
B
−
=
( )3
2
m
−
=
−
3
2
m =

26. Example 5: Find the slope and x & y intercepts of the
following equations.
A. -3 2 12x y+ =
A =
B =
C =
3−
2+
12
Slope x- intercept y-intercept
A
m
B
−
= - int
C
x
A
=
( )3
2
m
−
=
−
3
2
m =
3
- int
12
x =
−
- int 4x = −

27. Example 5: Find the slope and x & y intercepts of the
following equations.
A. -3 2 12x y+ =
A =
B =
C =
3−
2+
12
Slope x- intercept y-intercept
A
m
B
−
= - int
C
x
A
= -int
C
y
B
=
( )3
2
m
−
=
−
3
2
m =
3
- int
12
x =
−
- int 4x = −
- int
12
2
y =
- int 6y =

28. Example 5: Find the slope and x & y intercepts of the
following equations.
A. -3 2 12x y+ =
A =
B =
C =
3−
2+
12
Slope x- intercept y-intercept
A
m
B
−
= - int
C
x
A
= -int
C
y
B
=
( )3
2
m
−
=
−
3
2
m =
3
- int
12
x =
−
- int 4x = −
- int
12
2
y =
- int 6y =

29. Example 5: Find the slope and x & y intercepts of the
following equations.
B.
A =
B =
C =
5
3−
30
Slope x- intercept y-intercept
A
m
B
−
=
( )5
3
m
−
=
−
5
3
m =
5 3 30x y− =

30. Example 5: Find the slope and x & y intercepts of the
following equations.
B.
A =
B =
C =
5
3−
30
Slope x- intercept y-intercept
A
m
B
−
=
( )5
3
m
−
=
−
5
3
m =
5 3 30x y− =
- int
C
x
A
=
- int
30
5
x =
- int 6x =

31. Example 5: Find the slope and x & y intercepts of the
following equations.
B.
A =
B =
C =
5
3−
30
Slope x- intercept y-intercept
A
m
B
−
=
( )5
3
m
−
=
−
5
3
m =
5 3 30x y− =
- int
C
x
A
=
- int
30
5
x =
- int 6x =
-int
C
y
B
=
3
- int
30
y =
−
- int 10y = −

32. Example 5: Find the slope and x & y intercepts of the
following equations.
B.
A =
B =
C =
5
3−
30
Slope x- intercept y-intercept
A
m
B
−
=
( )5
3
m
−
=
−
5
3
m =
5 3 30x y− =
- int
C
x
A
=
- int
30
5
x =
- int 6x =
-int
C
y
B
=
3
- int
30
y =
−
- int 10y = −

33. 4 6 12x y+ = −
Example 5: Find the slope and x & y intercepts of the
following equations.
C.
A =
B =
C =
4
6
12−
Slope x- intercept y-intercept
A
m
B
−
=
( )4
6
m
−
=
2
3
m = −

34. 4 6 12x y+ = −
Example 5: Find the slope and x & y intercepts of the
following equations.
C.
A =
B =
C =
4
6
12−
Slope x- intercept y-intercept
A
m
B
−
=
( )4
6
m
−
=
2
3
m = −
- int
C
x
A
=
2
- int
1
4
x =
−
- int 3x = −

35. 4 6 12x y+ = −
Example 5: Find the slope and x & y intercepts of the
following equations.
C.
A =
B =
C =
4
6
12−
Slope x- intercept y-intercept
A
m
B
−
=
( )4
6
m
−
=
2
3
m = −
- int
C
x
A
=
2
- int
1
4
x =
−
- int 3x = −
-int
C
y
B
=
2
- int
1
6
y =
−
- int 2y = −

36. 4 6 12x y+ = −
Example 5: Find the slope and x & y intercepts of the
following equations.
C.
A =
B =
C =
4
6
12−
Slope x- intercept y-intercept
A
m
B
−
=
( )4
6
m
−
=
2
3
m = −
- int
C
x
A
=
2
- int
1
4
x =
−
- int 3x = −
-int
C
y
B
=
2
- int
1
6
y =
−
- int 2y = −

37. If an equation is written in standard form, you can
use the _______________ to graph the equation
quickly.
Ax By C+ =
x & y intercepts

38. Example 6: Graph the following equations.
-3 2 12x y+ =
A.
- int
C
x
A
= = 12
4
3−
=

39. Example 6: Graph the following equations.
-3 2 12x y+ =
A.
- int
C
x
A
= = 12
4
3−
=
-int
C
y
B
= 6
12
2
= =

40. Example 6: Graph the following equations.
-3 2 12x y+ =
A.
- int
C
x
A
= = 12
4
3−
=
-int
C
y
B
= 6
12
2
= =

41. 4 8x y− =
Example 6: Graph the following equations.
B.
- int
C
x
A
= = 8
4
2=

42. 4 8x y− =
Example 6: Graph the following equations.
B.
- int
C
x
A
= = 8
4
2=
-int
C
y
B
=
8
1
8=
−
= −

43. 4 8x y− =
Example 6: Graph the following equations.
B.
- int
C
x
A
= = 8
4
2=
-int
C
y
B
=
8
1
8=
−
= −

44. 4 6 12x y+ = −
Example 6: Graph the following equations.
C.
- int
C
x
A
= = 3
12
4
−
= −

45. 4 6 12x y+ = −
Example 6: Graph the following equations.
C.
- int
C
x
A
= = 3
12
4
−
= −
-int
C
y
B
=
6
2
12
=
−
= −

46. 4 6 12x y+ = −
Example 6: Graph the following equations.
C.
- int
C
x
A
= = 3
12
4
−
= −
-int
C
y
B
=
6
2
12
=
−
= −

47. 6 5 30x y− =
Example 6: Graph the following equations.
D.
- int
C
x
A
= =
30
6
5=

48. 6 5 30x y− =
Example 6: Graph the following equations.
D.
- int
C
x
A
= =
30
6
5=
-int
C
y
B
=
30
5
6=
−
= −

49. 6 5 30x y− =
Example 6: Graph the following equations.
D.
- int
C
x
A
= =
30
6
5=
-int
C
y
B
=
30
5
6=
−
= −