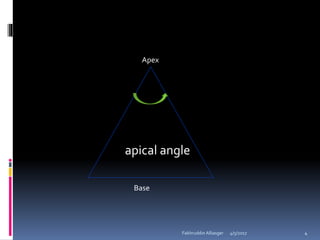
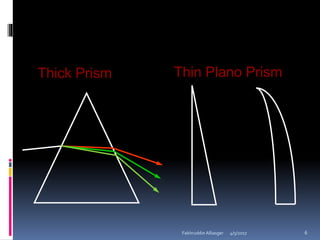
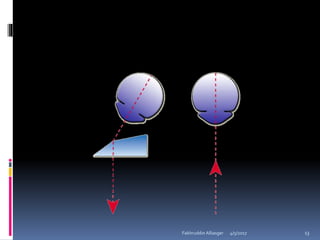
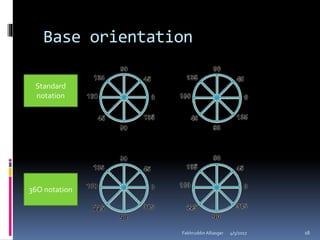
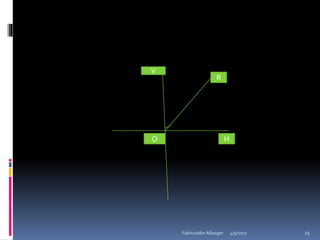
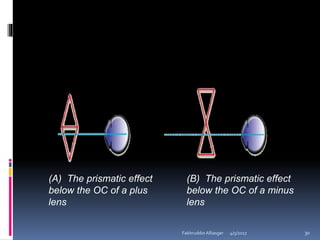
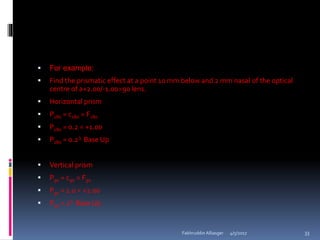
Ophthalmic prisms are thin prisms with an apical angle of less than 10-15 degrees. They are used in refractive corrections and can be prescribed for conditions like strabismus. The orientation of a prism, whether base-in or base-out, affects how the eye perceives an object through the prism. Prism power can be calculated using formulas like Prentice's rule and decompounded or recombined as needed for a prescription.

1. OPHTHALMIC PRISMS
Fakhruddin Aliasger
Lecturer, SPIO (a unit of Dr. Agarwal’s Eye Hospital)
4/5/2017Fakhruddin Alliasger 1

2. Prism
 A prism consists of two angled refracting
surfaces
 The simplest form of prism is two flat
surfaces coming together at an angle at the
top
 The point is called Apex of the prism
 The wider bottom of the prism is called the
base
4/5/2017Fakhruddin Alliasger 2

3.  The base of all prisms are thicker than the
apex
 The angle between the two refracting surface
of the prism is known as apical angle
4/5/2017Fakhruddin Alliasger 3

4. apical angle
Base
Apex
4/5/2017Fakhruddin Alliasger 4

5. Ophthalmic Prisms
 Ophthalmic prisms are, generally, thin
prisms.They have an apical angle of less than
10º to 15.
 Thin prism have no dioptric power but can be
combined with dioptric lenses in a refractive
correction.
 A curved thin prism of Plano dioptric power
has a front and back surface of equal and
opposite power.
4/5/2017Fakhruddin Alliasger 5

6. Thick Prism Thin Plano Prism
4/5/2017Fakhruddin Alliasger 6

7.  The orientation of the prism in front of the
eye will affect the position at which the eye
perceives any object to be viewed through
the prism. It is, therefore, important to
specify accurately the orientation of the
prism so that its effect on the eyes is known
when incorporated into a refractive
correction.
4/5/2017Fakhruddin Alliasger 7

8.  The orientation of a prism is specified in
terms of the position of the base and axis.
4/5/2017Fakhruddin Alliasger 8

9. Properties of prism
 The position of an object will appear to change
when viewed through a prism.
 White light incident on a thick prism will appear
to be dispersed into the colour spectrum when
emergent from the second surface.
 A prism displaying this phenomenon is often
known as a Newton prism.
 Dispersion is usually seen in thick prism i.e.. a
prism whose apical angle is greater than 15º to
20º.
4/5/2017Fakhruddin Alliasger 9

10. UNITS OF PRISM POWER
 The apical angle and the refractive index of the
prism determine its deviating power.
 Angular Units
 The deviation produced by the prism is
expressed in degrees or radians.
 Prism Dioptres
 One prism dioptre produces a deviation of one
unit at a plane 100 units from the prism
 The unit of prism dioptres is denoted  .Three
prism dioptres would be written as 3 
4/5/2017Fakhruddin Alliasger 10

11.  Centrads
 One Centrad produces a deviation of one unit
of arc at a distance of 100 units from the
prism
 The unit of Centrads is denoted .Thus,
three Centrads would be written as 3 .
4/5/2017Fakhruddin Alliasger 11

12. Prism in spectacles
 Prism is prescribed for various reasons,
strabismus (the most common reason),
convergence problems, hemianopia etc. Its
purpose is to deviate the path of the incident
light so that it corresponds with the visual
axes of the eyes. So, for example, if one eye
(the right in the side) has an exotropia base in
prism can be prescribed to bring the path of
light from the object being viewed back along
the visual axis.
4/5/2017Fakhruddin Alliasger 12

13. 4/5/2017Fakhruddin Alliasger 13

14. Orientation of prism
 The orientation of prism(s) in front of the eye(s) is
given by the position of the base.
 When facing the patient, the patient’s right eye is
on the examiner’s left side.
 Base out is denoted when the base is positioned
on the temporal side.When, a base out prism is
positioned in front of each eye, each prism will
have their base orientated at the temples of each
eye and the apices of the prisms will be pointing
towards the nose.
4/5/2017Fakhruddin Alliasger 14

15. L UPR UP
R OUT R & L
IN
L OUTR
DO
WN
L
DO
WN
4/5/2017Fakhruddin Alliasger 15

16.  Similarly, base in prism is denoted when the
base of the prism is orientated on the nasal
side of the eye and the apex is pointing
towards the temple
4/5/2017Fakhruddin Alliasger 16

17. Base orientation
 When prescribing prism it is, of course,
necessary to indicate the direction of the
prism base. While most cases will involve
prism in one of the four main directions, up,
down, in and out, oblique prism may also be
ordered.There are two accepted methods for
indicating the direction of an oblique prism.
4/5/2017Fakhruddin Alliasger 17

18. Base orientation
Standard
notation
36O notation
4/5/2017Fakhruddin Alliasger 18

19.  Standard notation:
 This is the same axis notation as used for the
axis of astigmatic lenses.This notation
requires further indication of the direction of
the base. For example, it is not sufficient to
order RE: 4  at 135.This could be either up
and out at 135 or down and in. So the
prescription needs the direction as well as the
angle.
4/5/2017Fakhruddin Alliasger 19

20.  360° notation:This system of notation is the
same as standard notation in the top two
quadrants but continues to 360 ° in the
bottom quadrants.This system requires no
other notation that the angle. So,
 RE: 4  at 135 would mean up and out, there is
no other possibility since down and in would
be RE: 4 at 315.
4/5/2017Fakhruddin Alliasger 20

21. Clinical consideration
 Due to the difference in thickness between the
base and the apex of a prism, refractive
corrections incorporating prism power for one
eye only, the spectacles may be dispensed with
the prism power split between the two eyes.This
is usually due to a noticeable and cosmetically
unacceptable difference in thickness between
the spectacle lenses if they were made up as
prescribed.
4/5/2017Fakhruddin Alliasger 21

22.  It is important that the effect on the eyes as a
pair is maintained when the prism power is
split between the spectacle lenses.This can
be achieved using the following rules.
 If the prismatic power is prescribed
monocularly in a refractive correction that is
similar between the two eyes, the prismatic
power should be split evenly.
4/5/2017Fakhruddin Alliasger 22

23.  Prism power with horizontal base direction
should have the same base direction in both
eyes
 Prism power with a vertical direction should
have opposite base directions in each eye,
with the base direction for the eye in which the
prism was originally prescribed remaining the
same.
4/5/2017Fakhruddin Alliasger 23

24. Compounding prism power
 The following correction is prescribed:
 R Plano 3  UP 4  IN
 L Plano
 The two prisms could be compounded i.e..
replaced by a single oblique prism.The resultant
prism would be positioned with its base between
the base directions of the two prescribed prisms.
The exact orientation of the single resultant
prism is determined by the power of the two
prescribed prisms.
 In the figure, OV represents the vertical prism,
OH the horizontal prism and OR the resultant
prism when the vertical and horizontal prisms
are compounded.
4/5/2017Fakhruddin Alliasger 24

25. HO
R
V
H
4/5/2017Fakhruddin Alliasger 25

26.  The exact position of the resultant prism can be
determined using Pythagoras’Theorem:
 (OR)2 = (OV)2 + (OH)2
 (OR)2 =( 3)2 + (4)2 = 25
 OR = 5 
 tan (ROH)= 3/4
 Angle ROH = tan-1(3/4) = 36.87º
 The resultant prism power is 5  orientated at
37 d
 R Plano 5  UP @ 37 L Plano
4/5/2017Fakhruddin Alliasger 26

27. Resolving prism power
 We have seen that a horizontal and vertical
prism prescribed in one eye can be compounded
to a single oblique prism. In the same way, a
single oblique prism can be simplified to two
orthogonal prisms.
 The following correction is prescribed:
 R Plano 4  UP @ 030
 L Plano
 Since the position of the single oblique prism is
known, simple trigonometry can be used to
simplify the prism to a horizontal and vertical
prism component:
4/5/2017Fakhruddin Alliasger 27

28.  sin 30 = (OV) / (OR)
 OV = 4.sin 30
 OV = 2  UP
 cos 30 = (OH) / (OR)
 OH = 4.cos 30
 OH = 3.46  OUT = 3.5  IN
 The final result would be written
 R Plano 2  UP 3.5  IN L Plano
4/5/2017Fakhruddin Alliasger 28

29. Prentice’s rule
 Prentice’s rule is the formula used to calculate
the decentration needed to create prism or
the prismatic effect of a lens at a given point.
For example, if we are required to find the
prismatic effect of a +5.00 D lens at a point 4
mm below the optical centre we use
Prentice’s rule. So,
 P = cF = 0.45 = 2  base up
4/5/2017Fakhruddin Alliasger 29

30. (A) The prismatic effect
below the OC of a plus
lens
(B) The prismatic effect
below the OC of a minus
lens
4/5/2017Fakhruddin Alliasger 30

31.  the prismatic effect at a point 4 mm below
the optical centre of a -4.00 D lens.
 P = cF = 0.44 = 1.6  base down
 Calculation of the prismatic effect for sphero-
cylinder lenses is the same if the prismatic
effect is required in a principal meridian. It is a
little more complex for oblique axes.
4/5/2017Fakhruddin Alliasger 31

32.  Axes of 90 and 180
 The decentration required to create prism
or the prismatic effect at any point on
cylinders and sphero-cylinders can be
determined using Prentice’s Rule, where:
 c is the distance from the optical centre for
each of the vertical and horizontal
meridians
4/5/2017Fakhruddin Alliasger 32

33.  For example:
 Find the prismatic effect at a point 10 mm below and 2 mm nasal of the optical
centre of a+2.00/-1.0090 lens.
 Horizontal prism
 P180 = c180  F180
 P180 = 0.2  +1.00
 P180 = 0.2 Base Up
 Vertical prism
 P90 = c90  F90
 P90 = 1.0  +2.00
 P90 = 2 Base Up
4/5/2017Fakhruddin Alliasger 33

34. Calculation of prismatic
effect in oblique cylinder
• The calculation of prismatic effect in oblique
cylinders requires a more complex set of
formulae. Before these formulae can be
applied certain notation and conventions
need to be established.
4/5/2017Fakhruddin Alliasger 34

35.  The notation:
 P is the point at which the prismatic effect is to be found
 x is the horizontal distance from optical centre in cm
 y is the vertical distance from optical centre in cm
 S is the sphere power of the prescription
 C is the cyl power
  is 180 - axis for the right eye and the axis for the left eye
 A,B and D are values used in the calculations of the prismatic
effect
 H is the horizontal prismatic effect
 V is the vertical prismatic effect
 It is H andV that we are aiming to find.That is, the horizontal and
vertical prismatic effects. 4/5/2017Fakhruddin Alliasger 35

36. Calculation of prismatic
effect in oblique cylinder
 The convention and condition are
 P is the position of measurement
 x is positive if P is in from the Optical centre
 x is negative if P is out from the Optical centre
 y is positive if P is up from the Optical centre
 y is negative if P is down from the Optical
centre.
4/5/2017Fakhruddin Alliasger 36

37.  Prismatic effect at p
 If H is positive the prismatic effect is base out
 If H is negative the prismatic effect is base in
 If V is positive the prismatic effect is base
down
 If V is negative the prismatic effect is base up.
4/5/2017Fakhruddin Alliasger 37

38.  Example: Calculate the prismatic effect
 8 mm down and 5 mm in from theOC of a
 RE:+5.00/-2.00 60
 The formulae are:
 A = S + Csin² = 5+ -2.00sin²120 = +3.5
 B =Csincos = -2.00sin120cos120 = 0.866
 D = S + Ccos² = 5+ -2.00cos²120 = +4.5
 H =Ax + By = 3.50.5 + 0.866 -0.8 = 1.057
 V = Bx + Dy = 0.8660.5 + 4.5 -0.8 = -3.167
 Therefore the prismatic effect at P is:
 1.057  base out
 3.167  base up
 Following from the conventions given in the previous slide, since H is positive the prism direction
is base out andV is negative so the direction is base up.
4/5/2017Fakhruddin Alliasger 38