This document is a beginner's guide to understanding spherical and cylindrical lenses, covering definitions, types, and characteristics of various lens forms. It details how to identify, mark, and write prescriptions for these lenses, as well as the effects of lens tilt on astigmatism and power calculations. Additionally, it provides examples and equations related to lens power adjustments.

1. Beginner’s Guide:
Spherical & Cylindrical Lenses
Rabindra Adhikary
ravinems@iom.edu.np

2. Lens: Definition
• A refracting media
enclosed by two
refracting surfaces
– At least one curved
surface

3. Types of Lens
• Contour of Lens Surface
– Depends upon the surfaces of revolution, which are formed
by rotating a plane curve about an axis with in its plane
• Lens Types
• Flat or plano
• Spherical
– Generated by rotating a circle or an arc about one of its diameter as an
axis of rotation
• Astigmatic Lenses
– Generated by rotating a straight line about another straight line that is
parallel to axis of rotation.
– Types
» Cross Cylinders
» Spherocylindrical
» Toric, Toroidal,
• Aspheric

4. Spherical (or Flat) lens -Spherical (or Flat) lens -
constant curvature at all meridiansconstant curvature at all meridians
Spherical (or Flat) lens -Spherical (or Flat) lens -
constant curvature at all meridiansconstant curvature at all meridians
CC

5. Cylindrical lens- constant curvatureCylindrical lens- constant curvature alongalong each meridian; varyingeach meridian; varying
curvaturescurvatures betweenbetween meridiansmeridians
Cylindrical lens- constant curvatureCylindrical lens- constant curvature alongalong each meridian; varyingeach meridian; varying
curvaturescurvatures betweenbetween meridiansmeridians
CC
Principal meridians -Principal meridians - axisaxis andand powerpower
Oblique meridian - “power”:Oblique meridian - “power”:
FFαα == FFCC sinsin22
αα
αα

6. Aspheric lens- varying curvatureAspheric lens- varying curvature alongalong each meridianeach meridian

7. Spherical Lens Forms
– Plano-concave
• often used for high minus Rx
– Plano-convex
• not used for ophthalmic
lenses

8. Spherical lens forms
– Bi-convex
• often used for high plus
Rx
– Bi-concave
• used rarely for very
high minus Rx

9. Spherical lens forms
– Periscopic (rarely used today)
• One of the first bent lenses
(convex front surface, concave
back surface)
• Plus Rx:
– -1.25 D base curve on back
• Minus Rx:
– +1.25 D base curve on front

10. Spherical lens forms
– Meniscus
• More Bent with +/- 6.00D BC
• Plus Rx:
– Base Curve = -6.00 Ds on the back
• Minus Rx:
– Base Curve = + 6.00 Ds on the front
• minus Rx
BC = -6.00
BC = +6.00

11. Optical Axis v. Optical Center of
a Lens
• Optical Axis
– Imaginary line connecting the
centers of curvature of 2 lens
surfaces
• Optical Center
– Point on the optical axis
intersected by the path of a
ray of light between the 2
surfaces
• (Essentially the point of no
prism)
– For any bent ophthalmic lens,
the optical center will fall
outside the lens

12. Optic
Axis
Plus Lens Minus Lens
Optical Center Optical Center

13. Optical CenterOptical CenterOptical CenterOptical Center
Optic AxisOptic AxisOptic AxisOptic Axis
Optical Pole;Optical Pole;
VertexVertex
Optical Pole;Optical Pole;
VertexVertex
Bent Ophthalmic Lens

14. Spherical Lens Identification &
Marking
• Straight edge test:
– Place the lens on straight surface.
– If lens is plano-
• Equal amount of light escapes beneath the edges
– If lens is cylindrical –
• Unequal light escape from the lens edge.
– At the Edge : ? Plus & Minus Lenses
• Cylindrical Lenses??

15. Spherical Lens Identification

16. Power measurement:
Neutralization
Foci meter

17. Cylindrical Lenses
• Cross Cylinders
• Spherocylinders
• Toric Lenses
Axis meridian = the meridian of least curvature
Power meridian = the meridian of maximum curvature

18. Types
Plano Cylinder Spherocylinder
Toric

19. Crossed-Cylinder Lenses
• Has plus cylinder ground on the front
surface and minus cylinder ground on the
back surface, with the axis 90° apart
• Available: +/- 0.25, 0.50, 0.75, 1.00

20. Spherocylindrical LensSpherocylindrical LensSpherocylindrical LensSpherocylindrical Lens

21. Astigmatic Lenses
• Example : +3.50 –150 x 180
– Astigmatic : No point focus
• Forms Line focuses
– Interval of Sturm
+3.50 D+3.50 D
+2.00 D+2.00 D
28.5 cm
28.5 cm
50 cm50 cm

22. Astigmatic Lenses
• Plano-cylinder
– one plano surface, one
cylindrical surface
plpl
plpl
FrontFront
plpl
-3-3
BackBack
plpl
-3-3
Compound:Compound:
pl -3.00 x090pl -3.00 x090

23. Astigmatic Lenses
• Toric
– one spherical surface, one cylindrical surface
with no plano meridian
+5+5
+5+5
FrontFront
-1-1
-4-4
BackBack
+4+4
+1+1
Compound:Compound:
+4.00 -3.00 x090+4.00 -3.00 x090

24. Astigmatic Lenses
• Bi-toric
– two cylindrical surfaces
– used in CL’s, but not spectacles
+5+5
+4+4
FrontFront
-3-3
-2-2
BackBack
+2+2
+2+2
Compound:Compound:
+2.00 sph!+2.00 sph!

25. Astigmatic Lenses
• Obliquely crossed cylinders
– Cylinders that are NOT 0 or 90 deg apart
require special solutions

26. Crossed-Cylinder Lenses
• Has plus cylinder ground on the front
surface and minus cylinder ground on the
back surface, with the axis 90° apart

27. Identifying Major Meridians &
Neutralization

28. Meridian - line along lens surfaceMeridian - line along lens surface
90 90
180 180
CCW
0
Specification of Cylinder AxisSpecification of Cylinder Axis

29. Specification of Cylinder Axis
• With the Rule –
– the minus axis is within 30° of the 180°
meridian
• Against the Rule –
– the minus axis is within of the 90° meridian
• Oblique cylinder –
– the minus axis is between 30° and 60° or
120° and 150°

30. Prescription Writing
• Spherical power first,
– then cylinder power, then the cylinder axis
– Eg: + 3.50 Ds / -1.50 Dc @ 1800
• Can be written in
– ? plus-cylinder or minus-cylinder
• Optical cross can help with visualization
Example +2.00Ds /+1.50 Dc x 090

31. Astigmatic Lenses
• Optical cross diagrams
FrontFront BackBack
Total PowerTotal Power
((ApproximateApproximate))
Example +2.00 +1.50 x 090

32. Three-Step Rule for Transposition
1. Add the sphere and cylinder power
algebraically
2. Change the sign of the cylinder
3. Rotate the cylinder axis 090°
–Eg:
–Minus Cylinder : + 3.50 Ds / -1.50 Dc @ 1800
–Plus Cylinder : +2.00 Ds/ +1.50 Dc x 0900

33. Pearls of Writing Standard Prescription
1. Right eye (OD) always first
2. Dioptric values always carried to 2nd
decimal point
3. Axis specified in three digits (x 016)
4. Fill in SPH or DS if no cylinder
• ? ? Do not use the degree ( ° ) symbol

34. 34
Astigmatism From Lens Tilt
• Tilting a lens
– new sphere becomes stronger than old
sphere
• minus lens becomes more minus
• plus lens becomes more plus
– cylinder will be induced
• same sign as the sphere
• axis equal to meridian of rotation

35. 35
Pantoscopic TiltPantoscopic Tilt
180180

36. 36
FaceformFaceform
(a.k.a. wrap, goggle effect)(a.k.a. wrap, goggle effect)
9090 9090

37. 37
Astigmatism From Lens Tilt
• Tilting a spherical lens
– new sphere power given by
FIC = FNS tan2
α
FNS = FOS (1 + )
sin2
α
2n
induced cylinder power given by

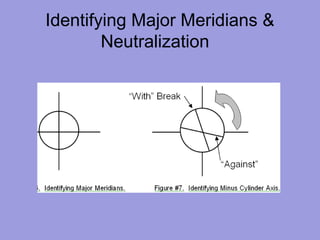
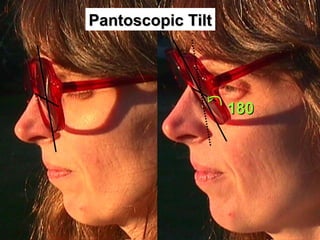
38. 38
Problem 3aProblem 3a
A +8.00 D lens has 20 degA +8.00 D lens has 20 deg
pantoscopicpantoscopic tilt. What is the newtilt. What is the new
power?power?
F = F
n
= +
N S O S (
s in
)
( ) (
s in
[ . ]
)
1
2
8 0 0 1
2 0
2 1 5 2 3
2
2
+
+
α
.
= +8.31 D

39. 39
Problem 3aProblem 3a (cont’d)(cont’d)
F = F
= + 8 . 3 1
I C N S t a n
( ) t a n
2
2
2 0
α
= +1.10 D
New lens power:
+8.31 +1.10 x180

40. 40
Problem 3bProblem 3b
A -10.00 D lens has 10 degA -10.00 D lens has 10 deg
faceformfaceform tilt. What is the newtilt. What is the new
power?power?
F = F
n
=
N S O S (
s in
)
( ) (
s in
[ . ]
)
1
2
1 0 0 0 1
1 0
2 1 5 2 3
2
2
+
− +
α
.
= -10.10 D

41. 41
Problem 3bProblem 3b (cont’d)(cont’d)
F = F
= 1 0 . 1 0
I C N S t a n
( ) t a n
2
2
1 0
α
−
= -0.31 D
New lens power:
-10.10 -0.31 x090

42. 42
9090 9090
180180
Astigmatism From Lens Tilt
• Tilting a cylindrical lens
– MUST have original cylinder power in
meridian of rotation
Transpose to:Transpose to:
x090x090
Transpose to:Transpose to:
x180x180

43. Spherical Equivalent
• “Average” power of an ophthalmic lens
– Determined by combining one-half the cylindrical
power with the spherical power
• EG: + 4.50 Ds/ -1.50 Dc x 040
• ?? Spherical Equivalent = ??

44. Spherical Equivalent:
Significance
• Adjusting the cylinder and sphere to
ease patient adaptation to a new
spectacle Rx
• Determining the total plus at near
– when a prebyope’s spectacle Rx is
changing