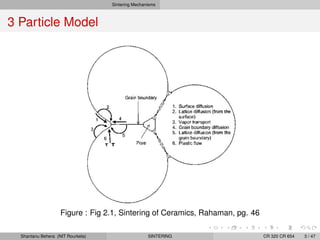
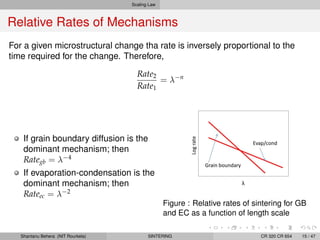
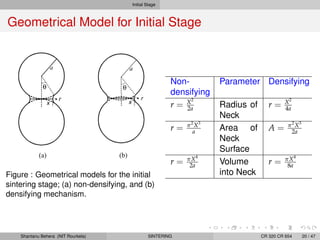
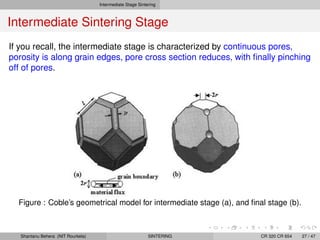
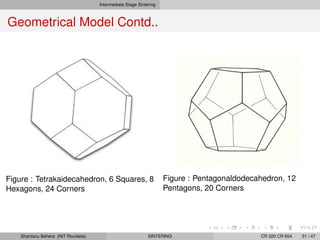
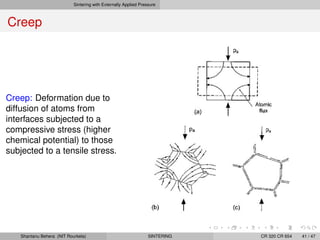
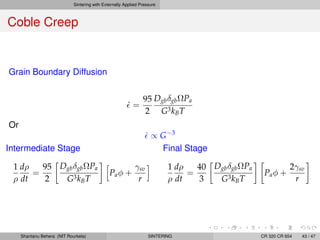
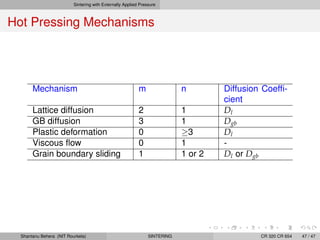
The document discusses the process of solid state sintering. It covers various sintering mechanisms like surface diffusion, lattice diffusion, and grain boundary diffusion. It describes the three stages of sintering - initial, intermediate and final. The initial stage involves rapid neck growth between particles through different mechanisms. The intermediate stage involves the development of continuous porosity along grain edges. During the final stage, isolated pores form at grain corners and gradually disappear. The document also presents kinetic equations to model neck growth and densification during the different sintering stages. It provides scaling laws relating sintering rates with particle size based on the dominant diffusion mechanism. Geometrical models are used to represent the microstructural changes during intermediate and final