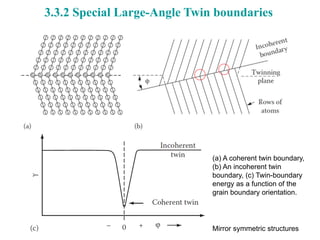
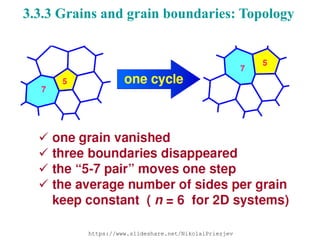
The document focuses on the phase transformations in metals and alloys, highlighting interfacial free energy, grain boundaries, and the kinetics of migration within crystal structures. It discusses various boundary types, including low-angle, high-angle, twist, and special boundaries, and their implications on microstructure and grain growth. Additionally, it covers interphase interfaces and coherency strains, providing insights into the behavior of different phases within metallic systems.

1. Textbook: Phase transformations in metals and alloys
(Third Edition), By: Porter, Easterling, and Sherif (CRC
Press, 2009).
Diffusion and Kinetics
Lecture: Crystal Interfaces and Microstructure
Nikolai V. Priezjev

2. Crystal Interfaces and Microstructure
► Interfacial Free Energy
► Solid-Vapor Interfaces
► Boundaries in Single-Phase Solids
(1) Low- & High-Angle Boundaries (2) Special Boundaries (3) Kinetics
► Interphase Interfaces in Solids
► Interface Migration
Reading: Chapter 3 of Porter, Easterling, Sherif
https://www.slideshare.net/NikolaiPriezjev

3. Basic Interface Types
https://www.slideshare.net/NikolaiPriezjev

4. 3.1 Interfacial Free Energy
Force per unit length!

5. 3.2 Solid - Vapor Interfaces
https://www.slideshare.net/NikolaiPriezjev

6. 3.2 Solid - Vapor Interfaces
https://www.slideshare.net/NikolaiPriezjev

7. High-indexed surface
2
2/|)|sin(cos aEsv  
Variation of surface energy as a function of 

8. High-indexed surface:  - plot

9. Equilibrium Crystal Surfaces
Heating up to the roughening transition.
A salt crystal (NaCl),
at 710 C. The six faces
along the crystal lattice
directions are flat
A gold crystal
at about 1000 C

10. 3.3 Boundaries in Single-Phase Solids: Tilt boundaries
https://www.slideshare.net/NikolaiPriezjev

11. 3.3 Low-angle tilt boundaries
Top view:
https://www.slideshare.net/NikolaiPriezjev

12. 3.3 Boundaries in Single-Phase Solids: Twist boundaries
https://www.slideshare.net/NikolaiPriezjev

13. 3.3 Low-Angle Twist boundaries
low-angle twist boundary:
⚬ atoms in crystal below
boundary, • atoms in
crystal above boundary.
Screw dislocation

14. Large-angle grain boundaries
Disordered grain boundary structure (schematic).

15. Large- & low-angle boundaries
Rafts of soap bubbles showing several grains of varying misorientation. Note that the boundary with the
smallest misorientation is made up of a row of dislocations, whereas the high-angle boundaries have a
disordered structure in which individual dislocations cannot be identified.

16. 3.3 Misorientation and boundary energy
Variation of grain boundary energy with misorientation (schematic).
random high-angle GBs
for low-angle
grain
boundaries
~ density of
dislocations
1/D~

17. 3.3.2 Special Large-Angle Twin boundaries
Twinned pyrite crystal group
Mirror symmetric structures

18. Nanotwin-governed toughening mechanism in hierarchically
structured biological materials. Shin et al. Nature 2016

19. Nanotwin-governed toughening mechanism in hierarchically
structured biological materials. Shin et al. Nature 2016
crack tip
opening
displacement
(CTOD)
transmission
electron
microscope
(TEM) images
aragonite
single crystal:
CaCO3

20. 3.3.2 Special Large-Angle Twin boundaries
(a) A coherent twin boundary,
(b) An incoherent twin
boundary, (c) Twin-boundary
energy as a function of the
grain boundary orientation.
Mirror symmetric structures

21. 3.3.2 Special Large-Angle Twin boundaries
Measured grain boundary energies for symmetric tilt boundaries in Al FCC (a) when
the rotation axis is parallel to 〈100〉, (b) when the rotation axis is parallel to 〈110〉.

22. 3.3.3 Equilibrium in Polycrystalline Materials
Microstructure of an annealed crystal of austenitic stainless steel (fcc)

23. 3.3.3 Grains and grain boundaries
https://www.slideshare.net/NikolaiPriezjev

24. 3.3.3 Grains and grain boundaries
https://www.slideshare.net/NikolaiPriezjev

25. 3.3.3 Grains and grain boundaries
https://www.slideshare.net/NikolaiPriezjev

26. 3.3.3 Grains and grain boundaries

27. 3.3.3 Grains and grain boundaries: Curvature
Two-dimensional grain boundary configurations. The arrows indicate the
directions boundaries will migrate during grain growth. Grain coarsening.
R
P
4

 = const
 = 120

28. 3.3.3 Grains and grain boundaries: Curvature
Two-dimensional cells of a soap solution illustrating the process of grain growth.
Air molecules in smaller cells diffuse through film into the larger cells. Numbers
are time in minutes.

29. 3.3.3 Grains and grain boundaries: Topology
https://www.slideshare.net/NikolaiPriezjev

30. 3.3.3 Grains and grain boundaries: Topology
https://www.slideshare.net/NikolaiPriezjev

31. 3.3.4 Thermally Activated Migration of GB
The atomic mechanism of boundary migration.
The boundary migrates to the left if the jump
rate from grain 1 → 2 is greater than 2 → 1.
Note that the free volume within the boundary
has been exaggerated for clarity.
The free energy of an atom during the
process of jumping from one grain to the
other.
r
V
G m

2

Gibbs-Thomson effect
mVGMv /

32. 3.3.5 Kinetics of Grain Growth
https://www.slideshare.net/NikolaiPriezjev

33. 3.3.5 Kinetics of Grain Growth
https://www.slideshare.net/NikolaiPriezjev

34. 3.3.5 Kinetics of Grain Growth
Pure Me, high T

35. 3.3.5 Kinetics of Grain Growth (in the presence of a second phase)
The effect of spherical particles on grain boundary migration.
Effect of second-phase particles on grain growth
Force from particle:
)45(sin)cos2( o
  rr
Dr
f
r
r
f
P



2
2
3
2
3
2

f
r
D
3
4
max 
particlesof
fractionvolumef
f
r
r
3
34
211
#




36. 3.4 Interphase Interfaces in Solids
Strain-free coherent interfaces. (a) Each crystal has a different chemical composition
but the same crystal structure. (b) The two phases have different lattices. Interfacial
plane has the same atomic configuration in both phases, e.g., (111) fcc & (0001) hcp.
ch (coherent) A-B bonds

37. 3.4 Interphase Interfaces in Solids
A coherent interface with slight mismatch
leads to coherency strains (or lattice
distortions) in the adjoining
lattices.
A semicoherent interface. The misfit
parallel to the interface is
accommodated by a series of edge
dislocations.



d
dd 


d
D 
mmJ500-200~
energylInterfacia
2-
A-B bonds
stch  ent)(semicoher
misfit dislocation
  Dst /1Interfacial energy:

38. 3.4 Interphase Interfaces in Solids
An incoherent interface. Interfacial plane has very different atomic configurations:
Two randomly oriented crystals. High interfacial energy ~500-1000 mJ/m2

39. 3.4.2 Fully Coherent Precipitates
(a) A zone with no misfit (O Al, • Ag, for example), (b) Electron micrograph of Ag-rich
zones in an Al-4 atomic % Ag alloy (× 300 000), (After R.B. Nicholson, G. Thomas and
J. Nutting, Journal of the Institute of Metals, 87 (1958-1959) 431.)
Ag rich ~10nm fcc regions
https://www.slideshare.net/NikolaiPriezjev

40. 3.4.2 Interphase Interfaces
A precipitate at a grain boundary triple point in an - Cu-In
alloy. Interfaces A and B are incoherent while C is semicoherent
(× 310). (After G.A. Chadwick, Metallography of Phase
Transformations, Butterworths, London, 1972.)

41. 3.4.3 Second Phase Shape: Misfit Strain Effects
The origin of coherency strains. The number of lattice points in the hole is conserved..
minimum sii GA
Fully coherent precipitates
Elastic strain energy
Condition for mechanical equilibrium
VGs  2
4 
shear modulus of matrix unconstrained misfit
Interfacial energy

42. 3.4.3 Second Phase Shape: Misfit Strain Effects
incoherent precipitates =
no coherency strains
The origin of misfit strain for an incoherent inclusion (no
lattice matching).
Volume misfit:
V
V

)/(
3
2 2
acfVGs  
shear modulus of matrix
The variation of misfit strain energy with ellipsoid shape
a
c
minimum sii GA
No coherency strains

43. 3.4.3 Second Phase Shape: Coherency Loss
The total energy of matrix + precipitate versus
precipitate radius for spherical coherent and non-
coherent (semicoherent or incoherent) precipitates.
chs rrG   232
4
3
4
4
Coherent precipitates:
Non-coherent precipitates:
)(40 2
stchs rG  
Critical radius:
2
4
3

st
critr 
chemical
interfacial
energy
structural
interfacial
energy
(due to misfit
dislocations)
Assuming:  st

1
critr
coherency strains

44. 3.4.4 Coherency Loss: Dislocation loop
Coherency loss for a spherical precipitate, (a) Coherent, (b) Coherency strains replaced
by dislocation loop, (c) In perspective.
semicoherent interfacecoherent interface
https://www.slideshare.net/NikolaiPriezjev