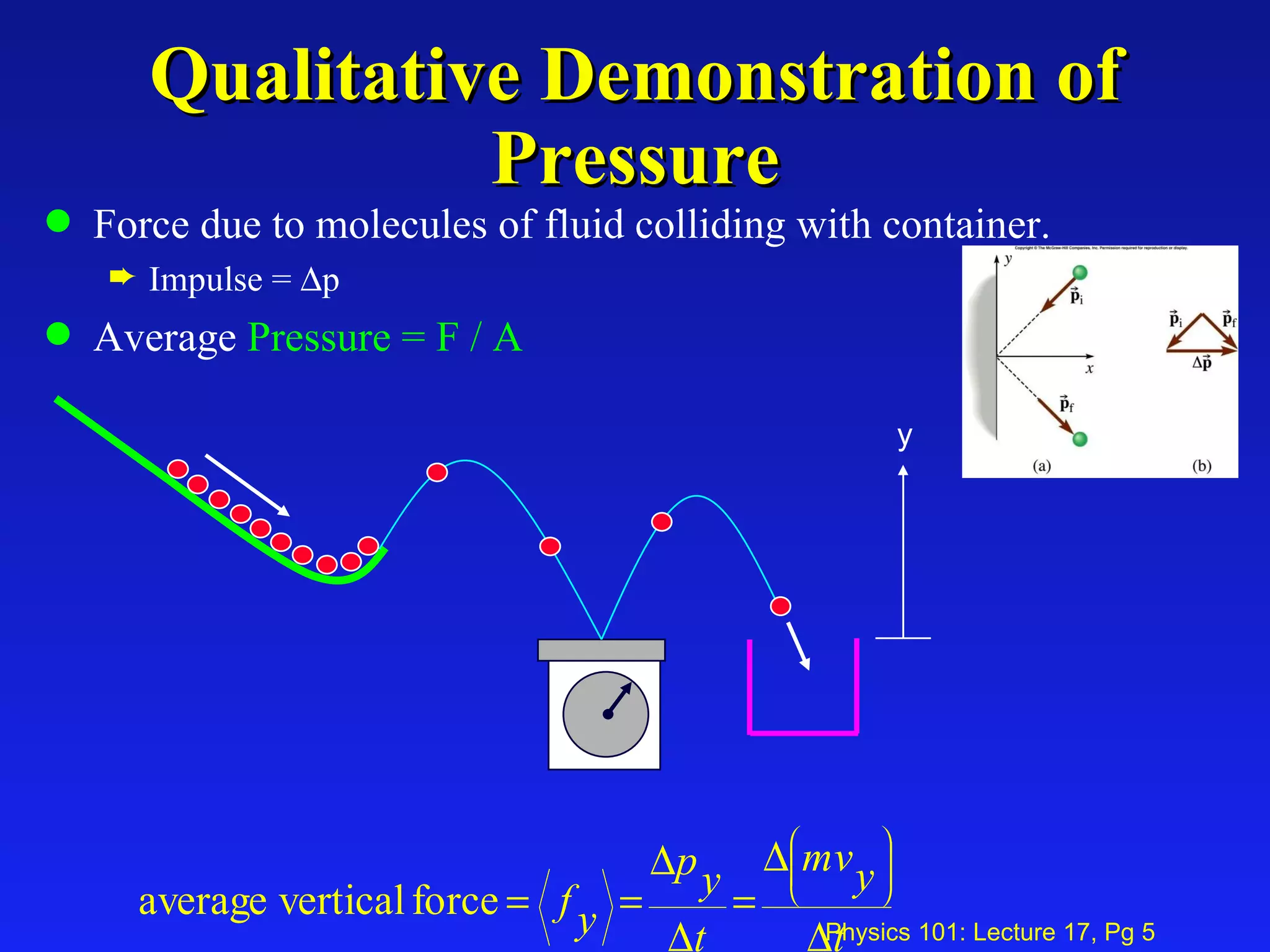
1) The document discusses fluid pressure and its relationship to depth, gravity, and buoyant forces. It explains that pressure is transmitted equally in all directions throughout a confined fluid. 2) Key concepts covered include Pascal's principle, how pressure depends on depth and density, and Archimedes' principle that the buoyant force equals the weight of fluid displaced. 3) Examples and demonstrations are provided to illustrate these fluid mechanics concepts.

1. Physics 101: Lecture 17 Fluids Exam III Exam 2 is Mon Oct. 25, 7pm Review is Sun Oct. 24, 8pm Sign up for conflict by tomorrow!

2. Homework 9 Help A block of mass M 1 = 3 kg rests on a table with which it has a coefficient of friction µ = 0.73 . A string attached to the block passes over a pulley to a block of mass M 3 = 5 kg . The pulley is a uniform disk of mass M 2 = 0.7 kg and radius 15 cm . As the mass M 3 falls, the string does not slip on the pulley. Newtons 2 nd Law 1) T 1 – f = M 1 a 1 T 1 R – T 3 R = I   T 3 – M 3 g = M 3 a 3 x y Notes: f =  M 1 g   = -a 1 / R I = ½ M R 2 a 1 = -a 3 Rewrite (a = a 1 ) T 1 = M 1 (a+  g) T 3 – T 1 = ½ M 2 a T 3 = M 3 (g – a) M 3 T 3 M 3 g M 2 T 3 T 1 M 1 N M 1 g T 1 f

3. Overview  F = m a  F Δ x = Change in Kinetic Energy  F Δ t = Change in momentum  = I   oday: apply these ideas to molecules in fluids

4. States of Matter Solid Hold Volume Hold Shape Liquid Hold Volume Adapt Shape Gas Adapt Volume Adapt Shape Fluids

5. Qualitative Demonstration of Pressure y Force due to molecules of fluid colliding with container. Impulse =  p Average Pressure = F / A

6. Atmospheric Pressure Basically weight of atmosphere! Air molecules are colliding with you right now! Pressure = 1x10 5 N/m 2 = 14.7 lbs/in 2 ! Example: Sphere w/ r = 0.1 m Spheres demo A = 4  r 2 = .125 m 2 F = 12,000 Newtons (over 2,500 lbs)! Can demo

7. Pascal’s Principle A change in pressure at any point in a confined fluid is transmitted everywhere in the fluid. Hydraulic Lift  P 1 =  P 2 F 1 /A 1 = F 2 / A 2 F 1 = F 2 (A 1 /A 2 ) lift demo Compare the work done by F 1 with the work done by F 2 A) W 1 > W 2 B) W 1 = W 2 C) W 1 < W 2 W = F d cos  W 1 = F 1 d 1 = F 2 (A 1 / A 2 ) d 1 but: A 1 d 1 = V 1 = V 2 = A 2 d 2 = F 2 V 1 / A 2 = F 2 d 2 = W 2

8. Gravity and Pressure Two identical “light” containers are filled with water. The first is completely full of water, the second container is filled only ½ way. Compare the pressure each container exerts on the table. A) P 1 > P 2 B) P 1 = P 2 C) P 1 < P 2 Under water P = P atmosphere +  g h 1 2 P = F/A = mg / A Cup 1 has greater mass, but same area

9. Pascal’s Principle (Restated) 1. Without gravity: Pressure of a confined fluid is everywhere the same. 2. With gravity: P = P atm +  g h Pressure of a fluid is everywhere the same at the same depth . [vases demo] In general: in a confined fluid, change in pressure is everywhere the same.

10. Dam ACT Two dams of equal height prevent water from entering the basin. Compare the net force due to the water on the two dams. A) F A > F B B) F A =F B C) F A < F B F = P A, and pressure is  gh. Same pressure, same area same force even though more water in B! B A A

11. Pressure and Depth Barometer: a way to measure atmospheric pressure p 2 = p 1 +  gh P atm - 0 =  gh Measure h, determine p atm example--Mercury  = 13,600 kg/m 3 p atm = 1.05 x 10 5 Pa  h = 0.757 m = 757 mm = 29.80” (for 1 atm) For non-moving fluids, pressure depends only on depth. h p 2 =p atm p 1 =0

12. Preflight Is it possible to stand on the roof of a five story (50 foot) tall house and drink, using a straw, from a glass on the ground? 70% 1. No 30% 2. Yes h p a p=0 The atmospheric pressure applied to the liquid will only be able to lift the liquid to a limited height no matter how hard you suck on the straw. Certainly trees have developed some mechanism to transport water from ground level, through their vascular tissues, and to their leaves (which can be higher that 50 feet) [interesting topic for a James Scholar paper…] Only Superman . . . or Kobe Bryant can do that. [demo]

13. Archimedes’ Principle Determine force of fluid on immersed cube Draw FBD F B = F 2 – F 1 = P 2 A – P 1 A = (P 2 – P 1 )A =  g d A =  g V Buoyant force is weight of displaced fluid!

14. Archimedes Example A cube of plastic 4.0 cm on a side with density = 0.8 g/cm 3 is floating in the water. When a 9 gram coin is placed on the block, how much does it sink below the water surface?  F = m a F b – Mg – mg = 0  g V disp = (M+m) g V disp = (M+m) /  h A = (M+m) /  h = (M + m)/ (  A) = (51.2+9)/(1 x 4 x 4) = 3.76 cm [coke demo] M =  plastic V cube = 4x4x4x0.8 = 51.2 g h mg F b Mg

15. Summary Pressure is force exerted by molecules “bouncing” off container P = F/A Gravity/weight affects pressure P = P 0 +  gd Buoyant force is “weight” of displaced fluid. F =  g V