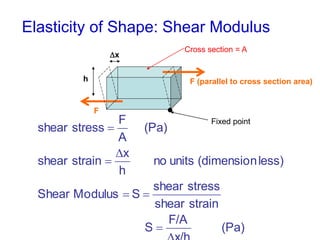
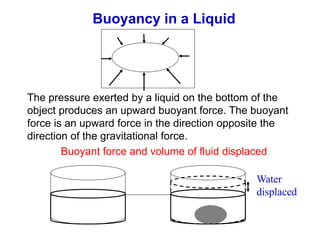
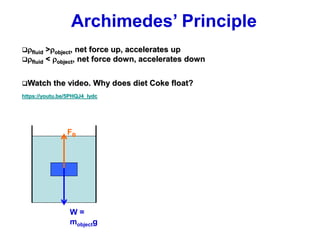
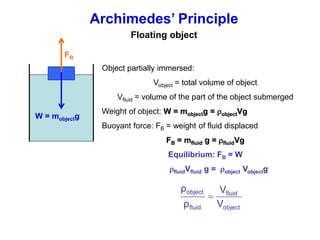
This document discusses key concepts about states of matter, properties of solids and fluids, and fluid dynamics. It defines solids, liquids, and gases, and explains how solids maintain a fixed shape and volume while liquids have a definite volume but not shape. It also covers elastic properties of solids including Young's modulus, shear modulus, and bulk modulus. Other topics include density, pressure, buoyancy, Archimedes' principle, fluid flow, Bernoulli's equation, and continuity equation.

1. Chapter 11: Solids (part1 of chap 11)
Chapter 13: Fluids

2. Properties of Solids
Properties of Fluids (Liquids and Gases)

3. States of Matter
Solid fixed shape and volume
Liquid definite volume, but not a definite shape
Gas neither shapes nor fixed volumes
Plasma (Highly ionized substance of positive
and negative charges- stars)
http://intro.chem.okstate.edu/1225/Lecture/Chapter13/State.html
http://intro.chem.okstate.edu/1225/Lecture/Chapter13/Microstates.html

4. Deformation of Solids
Solids have definite shape and volume, but are deformable. To change the
shape or size, one can apply a force. When force is removed, the object tends
to return to its original shape and size: Elastic behavior
Stress: force causing the deformation
Strain: measure of the degree of deformation
For small stresses, stress and strain are proportional. The proportionality
constant is called the elastic modulus and measure the stiffness of a material.
strain
stress
ModulusElastic 

5. Elasticity in Length: Young’s Modulus:
2
0
0
22
N/m
L/L
F/A
Y
straintensile
stresstensile
YModulussYoung'
less)(dimensionunitsno
L
L
straintensile
N/m1(pascal)1PaN/m
A
F
stresstensile






F (perpendicular to
cross section area)
Cross section = ALL0

6. Elasticity in Length: Young’s Modulus:
Pa20x10YSteel
Pa35x10YTungsten:9.1Table
stretchtodifficultareYlargewithmaterials
L/L
F/A
Y
10
10
0




Stress
(MPa)
strain
Elastic behavior
(straight line)
Elastic limit
Breaking point

7. Elasticity of Shape: Shear Modulus
Fixed point
h
x
Cross section = A
F (parallel to cross section area)
F
(Pa)
F/A
S
strainshear
stressshear
SModulusShear
less)(dimensionunitsno
h
x
strainshear
Pa)(
A
F
stressshear






8. Elasticity of Shape: Shear Modulus
Fixed point
h
x
Cross section = A
F (parallel to cross section area)
F
Pa8.4x10SSteel
Pa14x10STungsten:9.1Table
bendtodifficultareSlargewithmaterials
x/h
F/A
S
10
10





9. Volume Elasticity: Bulk Modulus
F (perpendicular to surfaces)
(Pa)
V/V
P
B
strainvolume
stressvolume
BModulusBulk
less)(dimensionunitsno
V
V
strainvolume
(Pa)P
A
F
stressvolume










10. Volume Elasticity: Bulk Modulus
ilitycompressibthecalledis
B
1
easilycompressnotdoesmodulusbulklargewithMaterial
compressedbecanliquidsandSolids
0VsodecreasesVand0Pincreases,PWhen
positivealwaysiswaythisdefinedB
Pa
V/V
P
B





11. Density and Specific Gravity
One of the most important property of materials.
If a mass m of a substance occupies a volume V, then the mass
density of the substance is the mass per unit volume
density = mass
volume
ρ = m/V
Typical Units: kg/m3 or g/cm3
1 kg /m3 = 0.001 g/cm3
Densities of some materials on page 262: (STP)
Water has a density of 1 g/cm3 (1000 kg/m3)
Another quantity that is commonly used is
weight density = weight weight per unit volume
volume
Specific density:
Specific density = density of substance
density of water

12. Pressure
Pressure is defined as the force exerted
over a unit area
pressure = force
area
P = F/A
Typical Units: pascal (Pa), 1 Pa = 1 N/m2.

13. Atmospheric Pressure
Like water, the atmosphere exerts a pressure. Just as water
pressure is caused by the weight of water, atmospheric
pressure is caused by the weight of air.
The pressure at sea level is about 15 lb/in2 (101.3 kPa). We
are not aware about the 15 lb force pushing every square
inch of our bodies, simply because the pressure inside our
bodies equals that of the surrounding air.
There is not net force on us.
Units: 1 atm = 1.013x103 N/m2 = 101.3 kPa
1 bar = 1.00x103 N/m2 = 100 kPa

14. Variation of Pressure with Depth
Fluid at rest in a container. Fluid exert force on object
(perpendicular to surface area)
F1 = F2
P1A = P2A
P1 = P2
All points at the same depth must be at the same
pressure
F1 F2
Small block of fluid
Small column of fluid
h
Mg
P0A
PA
3 forces on the column of fluid of height h
•P0A = force exerted by atmosphere
•Mg = force of gravity
•PA = force exerted by liquid below
Equilibrium: PA – Mg – P0A = 0
Since M = V= Ah, then Mg = gAh
P = P0 + gh

15. Variation of Pressure with Depth
When you swim under water, you can feel the pressure acting
against your eardrums. The deeper you go, the greater the
pressure.
The pressure exerted by a liquid depends on the depth.
If you swam in a liquid denser than water, the pressure would
be greater also.
The pressure exerted by a liquid depends on depth and
density
Liquid pressure = weight density x depth
P = ρg h
Pressure does not depend on amount of liquid!

16. Pressure gauges register the pressure over and above atmospheric
pressure
Absolute pressure = atmospheric pressure + gauge pressure
If a tire gauge registers 220 kPa, the absolute pressure within the tire is
220 kPa + 101 kPa = 321 kPa
P = P0 + ρgh
ρgh is the gauge pressure
Variation of Pressure with Depth

17. Pascal’s Principle
Since pressure depends on
depth and on the atmospheric
pressure P0, any increase in
pressure at the surface must be
transmitted in the fluid
Example 9.4
Example: Hydraulic lift
in
in
out
out
out
out
in
in
outin
F
A
A
F
A
F
A
F
PP




18. Measuring Pressure
Atmospheric pressure are measured with
instruments called barometers.
A mercury barometer where the weight of the
mercury column is balanced by atmospheric
pressure.
1 atm = pressure equivalent of a column of
mercury 76 cm in height at 00C
Hg = 13.595x103 kg/m3
g = 9.806 m/s2
h = 0.76 m
P0 = gh = 1.013x105 Pa = 1 atm

19. Buoyancy in a Liquid
The pressure exerted by a liquid on the bottom of the
object produces an upward buoyant force. The buoyant
force is an upward force in the direction opposite the
direction of the gravitational force.
Buoyant force and volume of fluid displaced
Water
displaced

20. Archimedes’ Principle
Any object completely or partially
submerged in a fluid is buoyed up by a force
whose magnitude is equal to the weight of
the fluid displaced by the object
FB
W =
mobjectg
Object completely immersed: Vobject = Vfluid = V
Weight of object: W = mobjectg = objectVg
Buoyant force: FB = weight of fluid displaced
FB = mfluid g = fluidVg
Fnet = FB – W = (fluid - object )Vg
fluid = object, equilibrium
fluid >object, net force up, accelerates up
fluid < object, net force down, accelerates down

21. Archimedes’ Principle
FB
W =
mobjectg
fluid >object, net force up, accelerates up
fluid < object, net force down, accelerates down
Watch the video. Why does diet Coke float?
https://youtu.be/5PHQJ4_lydc

22. Archimedes’ Principle
Floating object
FB
W = mobjectg
Object partially immersed:
Vobject = total volume of object
Vfluid = volume of the part of the object submerged
Weight of object: W = mobjectg = objectVg
Buoyant force: FB = weight of fluid displaced
FB = mfluid g = fluidVg
Equilibrium: FB = W
fluidVfluid g = object Vobjectg
object
fluid
fluid
object
V
V
ρ
ρ


23. Fluids in Motion: Fluid Dynamics
Smooth flow: streamline or
laminar (layered) flow
Turbulent flow
Different kinds of flow

24. Fluids in Motion: Fluid Dynamics
IDEAL FLUID
 fluid is non viscous. No internal friction force
between adjacent layers
fluid is incompressible: density is constant
fluid motion is steady: velocity, density and
pressure at each point in the fluid do not change in
time
fluid moves without turbulence

25. Fluids in Motion
Conservation of mass:
Region1: m1 = ρV1 = ρA1l1= ρA1v1 t
Region 2: m2 = ρV2 = ρA2l2= ρA2v2 t
Steady flow m1 = m2
Equation of Continuity: A1 v1 = A2 v2
The amount of fluid that enters one end of
the tube in a given time interval equals the
amount of fluid leaving the tube in the
same interval. Liquid is incompressible
ρ constant
Steady laminar flow

26. Bernoulli’s Equation
When the speed of a fluid
increases, pressure in the fluid
decreases.
Bernoulli's principle holds only
for steady flow. If the speed is
too great, the flow may become
turbulent.
Examples:
•Atmospheric pressure
decreases in a tornado or
hurricane.
•A spinning ball curves up
Airplane wing
Ball in jet of air
Low pressure
High pressure
lift

27. Bernoulli’s Equation: conservation
of energy applied to an ideal fluid
P1 + ½ ρv1
2 + ρgy1 = P2 + ½ ρv2
2 + ρgy2
P + ½ ρv2 + ρgy = constant
Kinetic energy
Potential energy