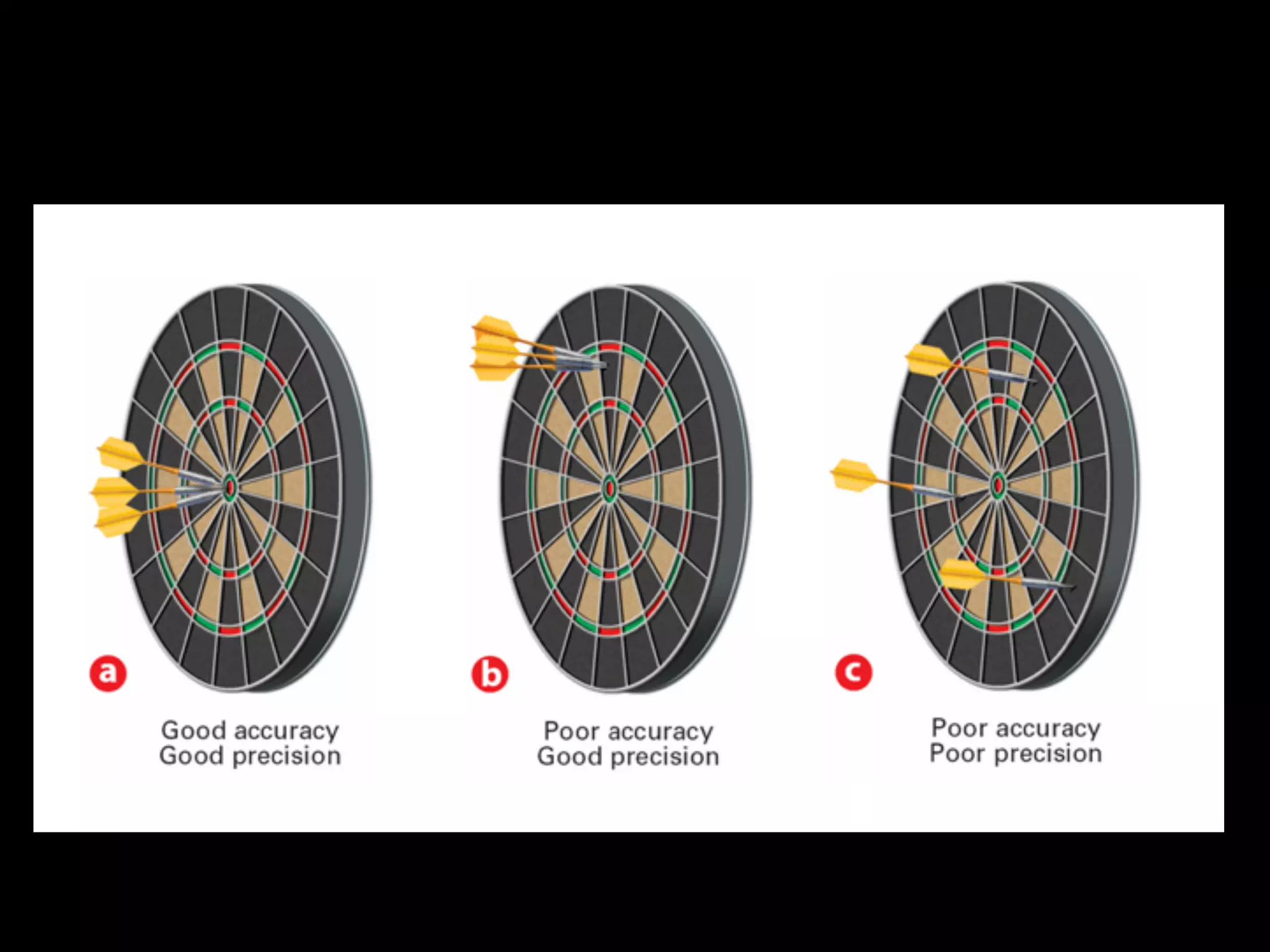
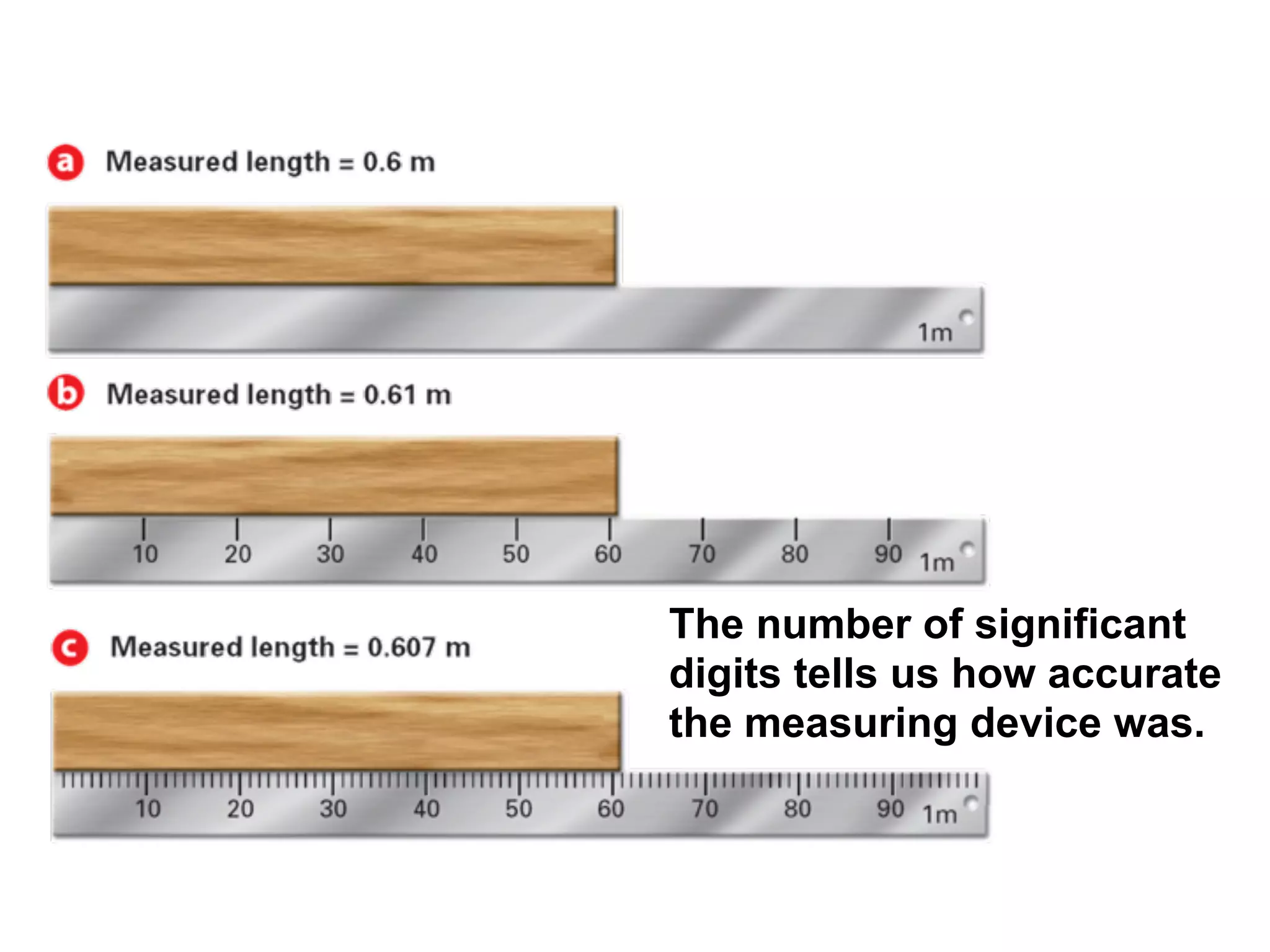
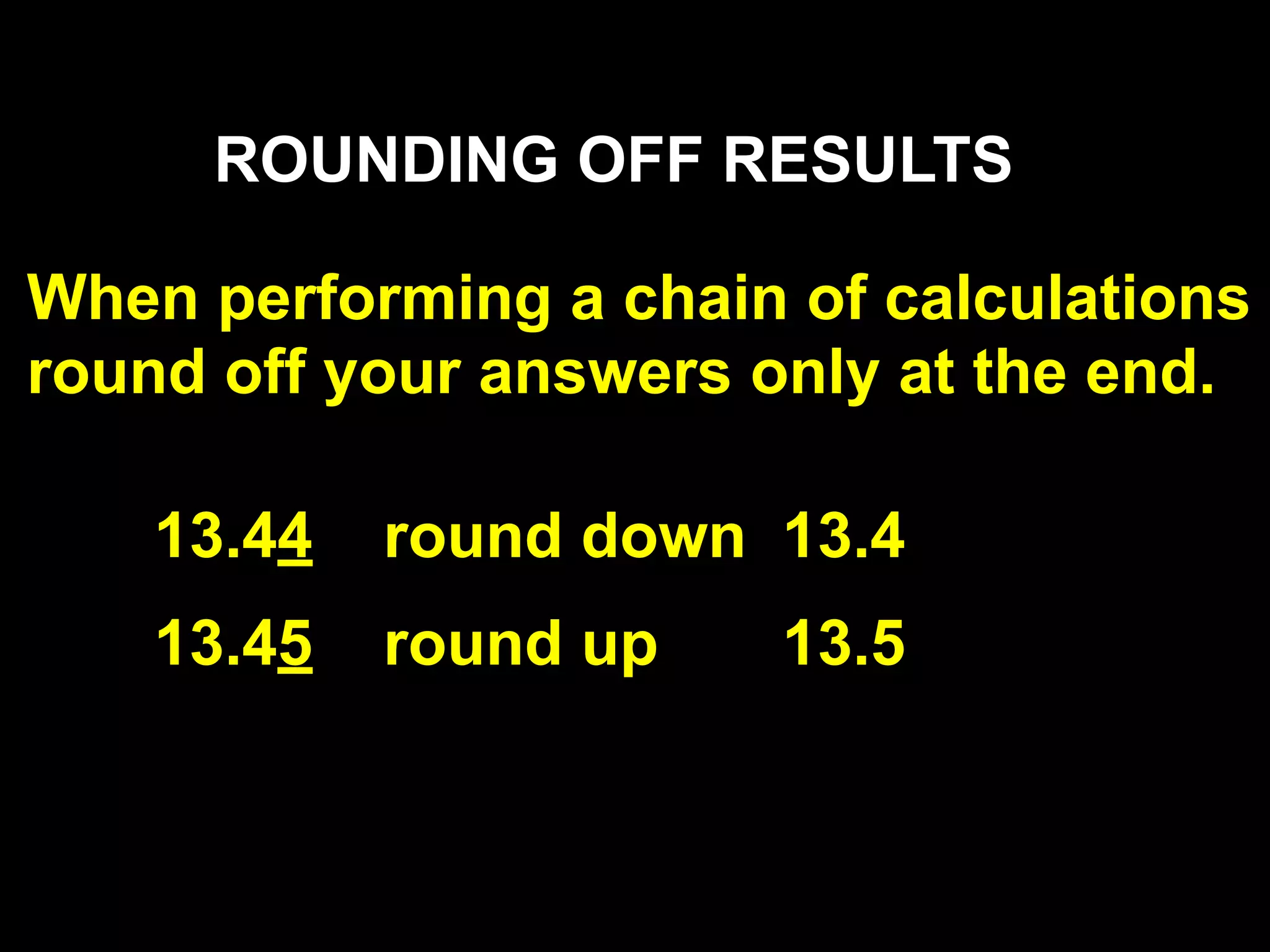
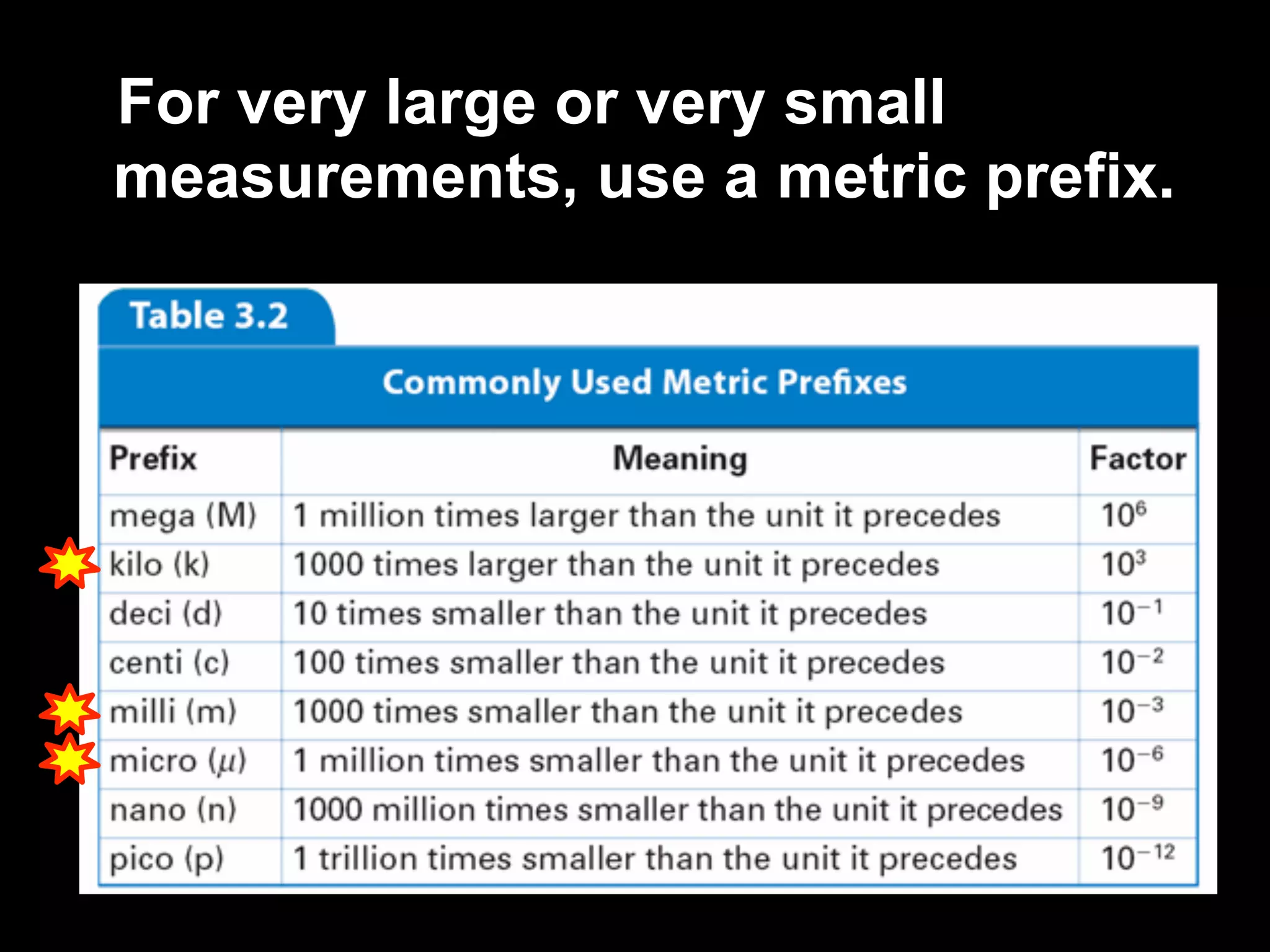
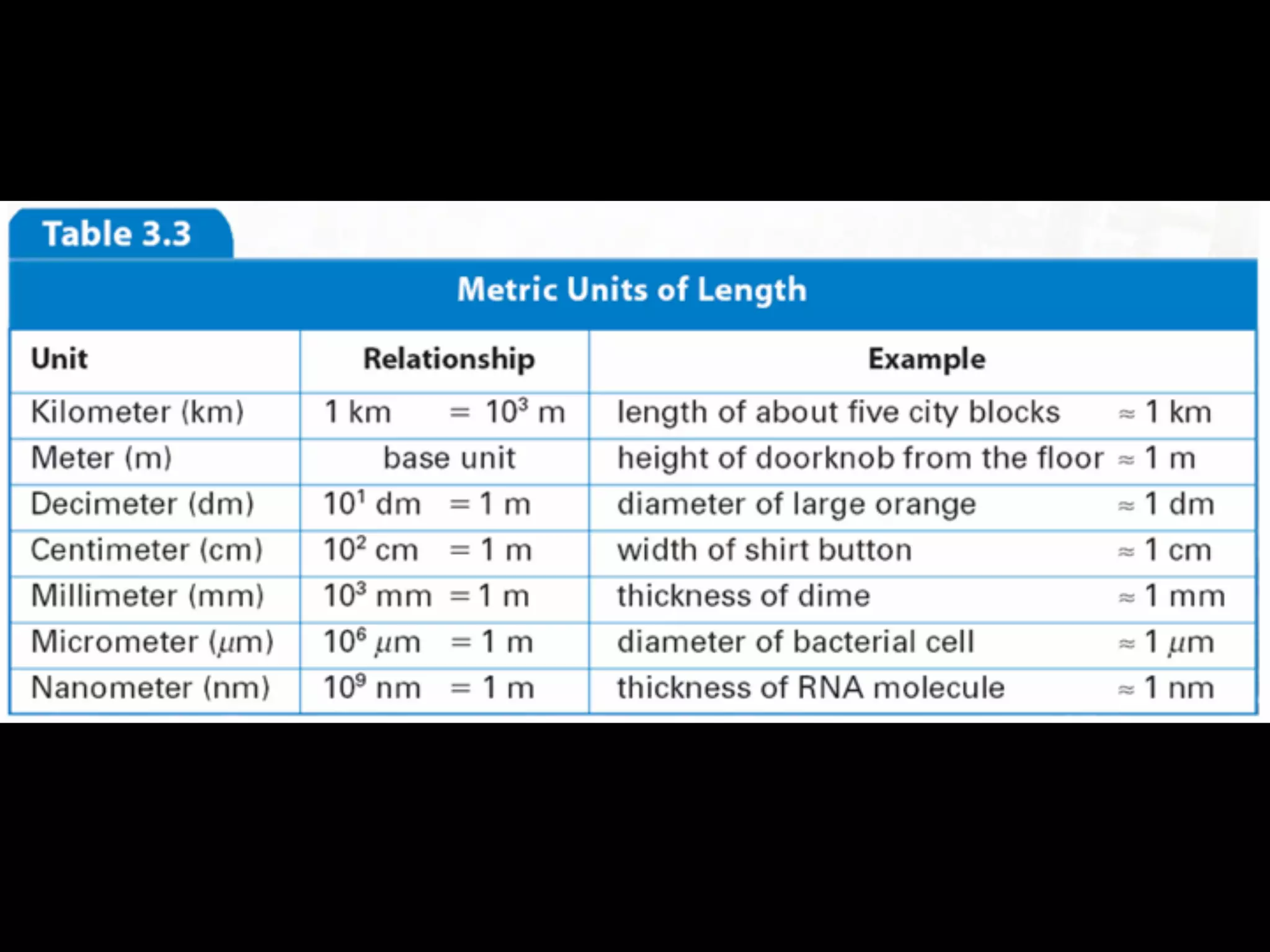
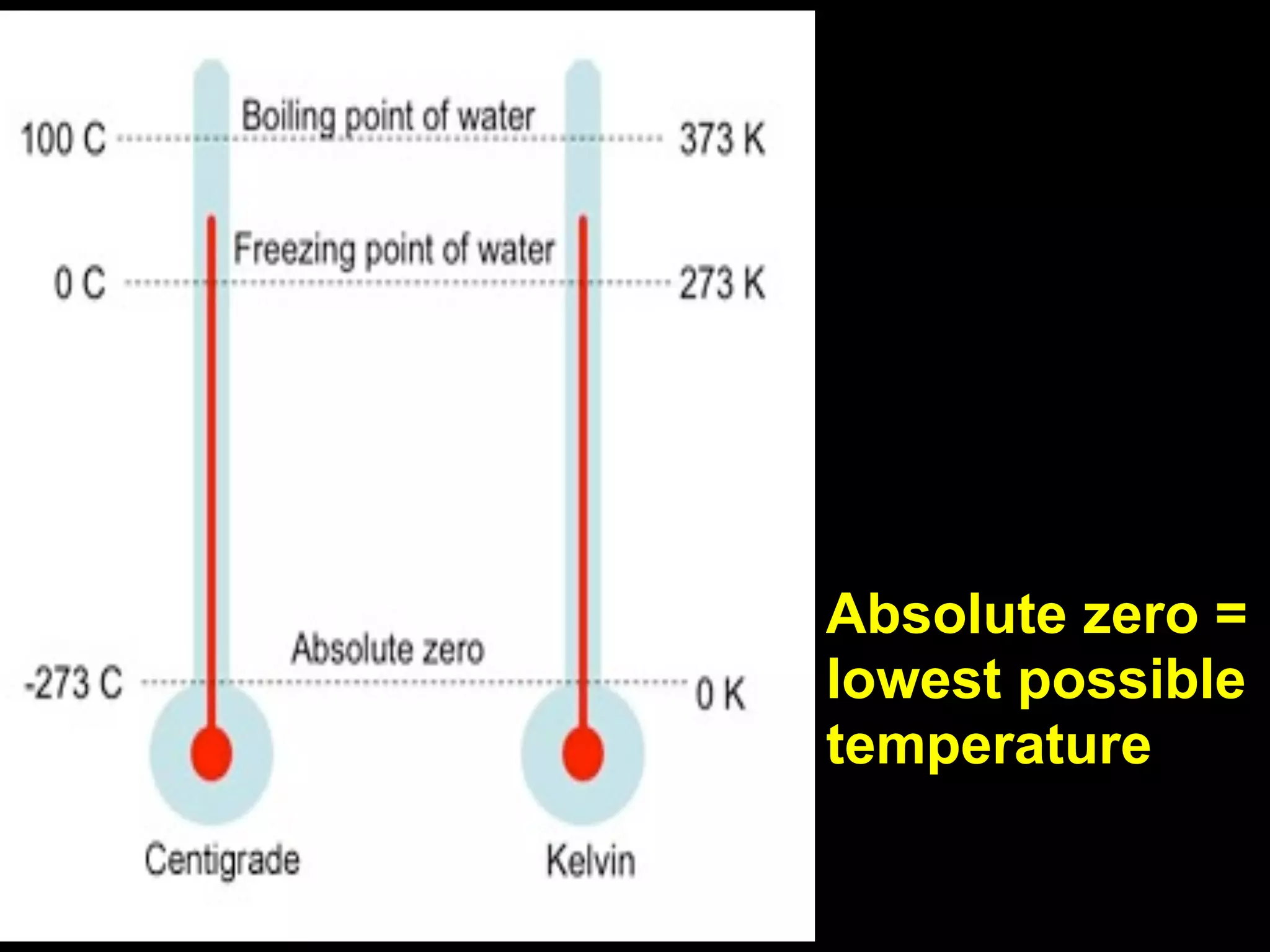
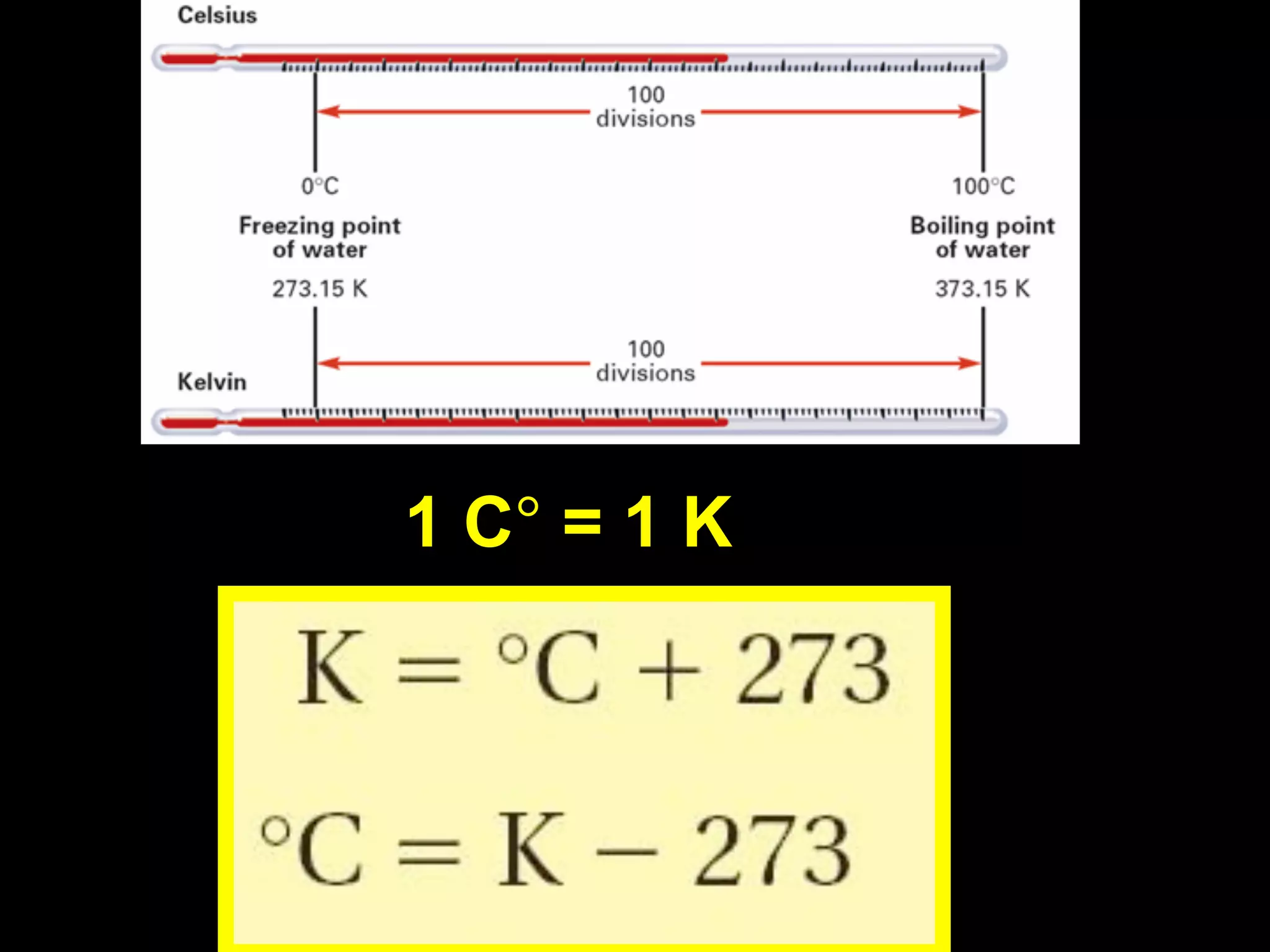
This document discusses scientific notation and units of measurement. It introduces scientific notation as a way to represent very large or small numbers between 1 and 10 with an exponent. Accuracy refers to how close a measurement is to the true value, while precision refers to the agreement between repeated measurements. Significant figures indicate the precision or number of digits known in a measurement. Calculations are only as precise as the least precise input measurement. Proper rounding of results is also covered. Standard International (SI) units for length, mass, temperature, time, and amount are defined. Common metric units for volume, mass, and temperature are also discussed.

1. Lecture 3.1 and 3.2-
Measurements

2. SCIENTIFIC NOTATION
is used to represent very large
or very small numbers

3. SCIENTIFIC NOTATION
6.02 x 1023

4. SCIENTIFIC NOTATION
6.02 x 1023
must be
between
1-10

5. SCIENTIFIC NOTATION
6.02 x 1023
must be The power of ten
between determines the size of
1-10 the number

6. SCIENTIFIC NOTATION
6.02 x 1023
must be The power of ten
between determines the size of
1-10 the number
Positive power = big number(greater than 10)
Negative power = small number(less than one)

7. SCIENTIFIC NOTATION
6.02 x 1023
must be The power of ten
between determines the size of
1-10 the number
Positive power = big number(greater than 10)
Negative power = small number(less than one)
EX. 0.00567g = 5.67 x 10-3g a small number
437,850g = 4.3785 x 105g a large number

8. To convert from standard notation to
scientific notation move the decimal point
to make a number between 1 and 10 then
count how many spaces you moved it.
positive
because it
is a big
number
negative
because it is a
small number

9. Accuracy and Precision
• Accuracy measures how close a
measurement comes to the actual
value.
• Precision measures how close a
series of measurements are to each
other.

10. 3.1

11. Just because a measuring device
works, you cannot assume it is
accurate.
The scale has not been properly zeroed,
so the reading obtained for the person’s
weight is inaccurate.

12. Significant digits
When measuring we record all
certain digits plus one uncertain
digit

13. Significant digits
When measuring we record all
certain digits plus one uncertain
digit, so there is always some
degree of uncertainty
in measurement.

14. Significant digits
When measuring we record all
certain digits plus one uncertain
digit, so there is always some
degree of uncertainty
in measurement.
In science we account
for this by using
significant digits or
significant figures

15. The more significant digits in a
measurement the more accurate the
measuring device was.

16. The more significant digits in a
measurement the more accurate the
measuring device was.

17. The more significant digits in a
measurement the more accurate the
measuring device was.

21. The number of significant
digits tells us how accurate
the measuring device was.

22. Reporting calculations with the
correct number of significant digits

23. Reporting calculations with the
correct number of significant digits
Our calculations are only as
precise as our least precise
measurement.

24. Our calculations are only as precise as
our least precise measurement

25. Our calculations are only as precise as
our least precise measurement
If 30 beans have a mass of
17.3g what is the average mass?

26. Our calculations are only as precise as
our least precise measurement
If 30 beans have a mass of
17.3g what is the average mass?
17.3g/30 =

27. Our calculations are only as precise as
our least precise measurement
If 30 beans have a mass of
17.3g what is the average mass?
17.3g/30 = 0.576666666666666666g

28. Our calculations are only as precise as
our least precise measurement
If 30 beans have a mass of
17.3g what is the average mass?
17.3g/30 = 0.576666666666666666g
Does it really make sense to claim
such precision when we only
measured out to one tenth of a gram?

29. 17.3g/30 = 0.576666666666666666g
The measurement has
three significant digits

30. 17.3g/30 = 0.576666666666666666g
The measurement has
three significant digits
The measurement only has
3 significant digits so the answer
should have only 3 significant
digits.

31. 17.3g/30 = 0.576666666666666666g
The measurement has
three significant digits
The measurement only has
3 significant digits so the answer
should have only 3 significant
digits.
0.577g

32. ROUNDING OFF RESULTS
When performing a chain of calculations
round off your answers only at the end.
13.44 round down 13.4
13.45 round up 13.5

33. 3.1 Using and Expressing
Measurements
A measurement is a quantity that
has both a number and a unit.

34. Measuring with SI Units
5 of the 7 S.I. base units are used by
chemists
m meter (length)
kg kilogram (mass)
K kelvin (temperature)
s second (time)
mol mole (quantity)

35. 3.2 Units and Quantities
For very large or very small
measurements, use a metric prefix.

36. 3.2 Units and Quantities

37. Units of Volume
3.2 Units and Quantities
The SI unit of volume is the cubic meter (m)3,
which is the amount of space occupied by a
cube that is 1 m along each edge.
A more convenient unit of volume for
everyday use is the liter, a non-SI unit.

38. Units of Volume
3.2 Units and Quantities
The SI unit of volume is the cubic meter (m)3,
which is the amount of space occupied by a
cube that is 1 m along each edge.
A more convenient unit of volume for
everyday use is the liter, a non-SI unit.
A liter (L) is the volume of a cube
that is 10 centimeters (10 cm)
along each edge.
10 cm × 10 cm × 10 cm = 1000 cm3 = 1 L

39. 3.2 Units and Quantities
Common metric units of volume
include the liter, milliliter (aka cubic
centimeter), and microliter.

40. 3.2 Units and Quantities
Common metric units of mass
include kilogram, gram, milligram,
and microgram.

41. 3.2 Units and Quantities
Scientists commonly use two
equivalent units of temperature,
the degree Celsius and the kelvin.

42. Absolute zero =
lowest possible
temperature

43. 3.2 Units and Quantities
1 C° = 1 K

46. 3.2 Units and Quantities

47. 3.2 Units and Quantities
Energy is the capacity to do
work or to produce heat.

48. 3.2 Units and Quantities
The joule (J) is the SI unit of
energy.
One calorie (cal) is the quantity
of heat that raises the
temperature of 1 g of pure water