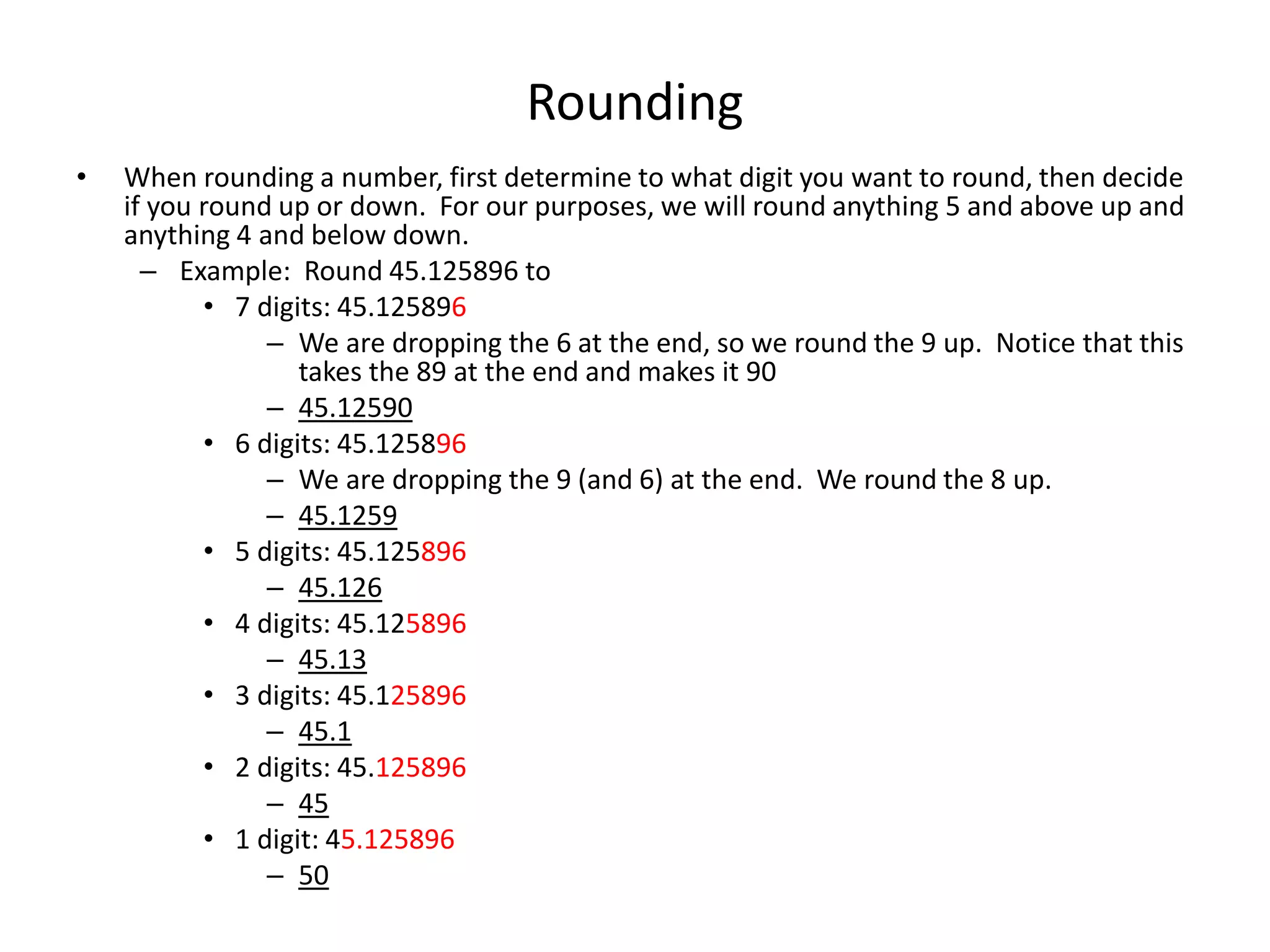
This document discusses significant digits and proper rounding techniques in calculations. It begins by explaining how to round numbers to various places and the rules for determining significant digits. It emphasizes that the accuracy of a calculation is limited by the least accurate initial value. For addition and subtraction, the answer should be rounded to the least number of decimal places. For multiplication and division, the answer should be rounded to the same number of significant digits as the least accurate factor or dividend. Examples are provided to demonstrate rounding calculations correctly according to these rules.

1. Significant Digits
or How and When to Round

2. Rounding
• When rounding a number, first determine to what digit you want to round, then decide
if you round up or down. For our purposes, we will round anything 5 and above up and
anything 4 and below down.
– Example: Round 45.125896 to
• 7 digits: 45.125896
– We are dropping the 6 at the end, so we round the 9 up. Notice that this
takes the 89 at the end and makes it 90
– 45.12590
• 6 digits: 45.125896
– We are dropping the 9 (and 6) at the end. We round the 8 up.
– 45.1259
• 5 digits: 45.125896
– 45.126
• 4 digits: 45.125896
– 45.13
• 3 digits: 45.125896
– 45.1
• 2 digits: 45.125896
– 45
• 1 digit: 45.125896
– 50

3. Misconception alert!
• Notice on the last example when rounding to one digit that the answer
was 50 and not 5. When rounding you can drop digits to the right of a
decimal, but cannot drop them to the left. You make the digits that you
are rounding off that are to the left of a decimal zeros.
– Round 654
• To 2 digits
– 650
• To 1 digit
– 700

4. Maintaining Accuracy is the Key when Choosing
to Round
• Let’s compare three different measurements of mass in grams (g) that are
made with three different balances:
– 2.5 g
– 2.53 g
– 2.528 g
• Notice how each successive measurement has more digits, which means that
the measurement is more accurate.
• Notice how for the first mass of 2.5, we do not know what comes after the 5
(without looking at the other masses). Do not think it is a zero. If it was a
zero, we would have written a zero there. Since it could be greater or less we
say the 5 has some uncertainty to it. All measurements (except counting) have
some uncertainty to them. If we had an even better balance, we would see
that the mass is 2.5276 g, though at no point can we say it is exact.

5. In calculations, you cannot give a result more
accurate than the measurements you began with.
• If the object measured on the previous slide has a volume of 2.345 mL we
can calculate the density with the different masses (mass divided by volume)
– With 2.5g: 𝐷 =
2.5𝑔
2.345𝑚𝐿
= 1.066098081 𝑔
𝑚𝐿 = 1.1 𝑔
𝑚𝐿
– With 2.53g: 𝐷 =
2.53𝑔
2.345𝑚𝐿
= 1.078891258 𝑔
𝑚𝐿 = 1.08 𝑔
𝑚𝐿
– With 2.528g: 𝐷 =
2.528𝑔
2.345𝑚𝐿
= 1.07803838 𝑔
𝑚𝐿 = 1.078 𝑔
𝑚𝐿
• Notice how we rounded the answers differently. This was done to reflect the
different accuracies of the masses used. Since the first mass was only
accurate to two digits, we rounded our answer to two digits. Our second
mass was accurate to three digits, so our calculation must be accurate to
three digits. In the fourth, both the mass and the volume have four digits, so
our density is accurate to four.
• The result of a calculation can be no more accurate than the least accurate
number you started with.

6. Counting accurate (significant) digits.
• The digits we count as accurate digits in a measurement are called significant
digits.
• Counting significant digits is easy:
– All non-zero numbers count as significant digits
– Zeros count unless they
• Are at the very beginning of a number
• Are at the end of a number that does not have a decimal
• Examples:
– 1.205 – all numbers are significant, so 4 significant digits
– 0.0010 – the zeros at the beginning are not significant, but he ones at the
end are since there is a decimal, so 2 significant digits
– 2050 – the zero at the end is not significant since there is no decimal. 3
significant digits
– 200. – since there is a decimal, the zeros at the end are significant. 3
significant digits

7. Pause and practice
• Underline the significant digits in the following numbers and indicate how
many significant digits they have.
– 1.00050
– 8500
– 0.000502
– 500.0

8. Pause and practice answers
• Underline the significant digits in the following numbers and indicate how
many significant digits they have.
– 1.00050
• 6 significant digits
– 8500
• 2 significant digits (zeros at the end with no decimal do not count)
– 0.000502
• 3 significant digits (zeros at the beginning do not count)
– 500.0
• 4 significant digits

9. Calculations with significant digits
• From the example with density, we saw that with division we round the
answer to the number of significant digits that our least accurate initial
number had – least significant digits. We do the same thing with
multiplication.
• More example:
–
0.0450 𝑔
0.23𝐿
= 0.195652174 𝑔
𝐿 = 0.20 𝑔
𝐿
• 0.0450 has 3 significant digits, 0.23 has 2 significant digits
• 2 is smaller than 3, so our answer must be rounded to 2 significant
digits.
– 2.03 𝑐𝑚 × 1.011 𝑐𝑚 = 2.05233 𝑐𝑚2 = 2.05𝑐𝑚2
• 2.03 has 3 significant digits, 1.011 has 4, our answer must be
rounded to 3.

10. Calculations Continued – Addition and
Subtractions
• With addition and subtraction, the rule for rounding is to round to the
decimal place of the number with the smaller number of decimal places.
– Example
• 2.5 + 3.451 = 5.951 = 6.0
– 2.5 has only 1 digit after the decimal and 3.451 has 3. 1 is less
than 3, so our answer can only have one digit after the
decimal
– Example
• 3.251 – 2.6 = 0.651 = 0.6
– 3.521 has 3 digits after the decimal. 2.6 has 1. Our answer
can have 1 digit after the decimal.

11. Misconception Alert
• Many students like to use one rule for everything. Do not! There are two
different rules.
• Do not mix up your rules. They are different.
– Multiplication and division give an answer with the least significant
digits.
– Addition and Subtraction give an answer with the least number of
decimal places. This rule does not care about total significant digits.

12. Pause and Practice
• What are the answers to the following rounded to the correct accuracy?
• 0.025 + 1.3 =
• 0.025 x 1.3 =
• 503 – 245.62 =
• 503 / 245.62 =

13. Pause and Practice
• What are the answers to the following rounded to the correct accuracy?
• 0.025 + 1.3 = 1.3
• 0.025 x 1.3 = 0.033
• 503 – 245.62 = 257
• 503 / 245.62 = 2.05

14. Try the exercises
A final note: In future exercises you will need to be mindful of significant
digits. While Blackboard will not grade based on significant digits, if you
round too much your answer will not be accepted.