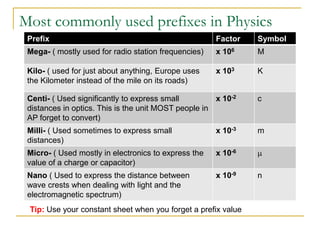
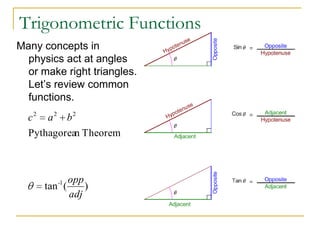
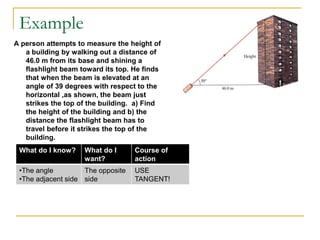
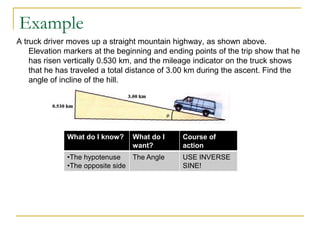
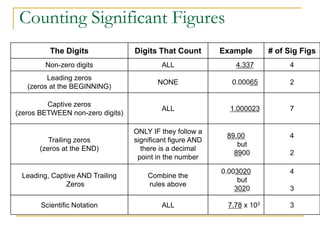
Measurement and units are important concepts in physics. The document discusses the SI system of units including fundamental units like meters, kilograms, and seconds. It also covers prefixes that are used with SI units to denote larger or smaller quantities. Derived units and dimensional analysis are introduced. The document also discusses measurement precision, significant figures, scientific notation, and estimating order of magnitude. Calculating with measurements and expressing uncertainty are also summarized.

1. Measurement in Physics
AP Physics C

2. SI units for Physics
The SI stands for "System International”. There are 3
fundamental SI quantities we will be using this
semester. They basically breakdown like this:
SI Quantity SI Unit
Length Meter
Mass Kilogram
Time Second
Of course there are many other units to consider. Many times, however, we
express these units with prefixes attached to the front. This will, of course,
make the number either larger or smaller. The nice thing about the prefix is
that you can write a couple of numbers down and have the unit signify
something larger.
Example: 1 Kilometer – The unit itself denotes that the number is actually
larger than "1" considering fundamental units. The fundamental unit would
be 1000 meters

3. Most commonly used prefixes in Physics
Prefix Factor Symbol
Mega- ( mostly used for radio station frequencies) x 106 M
Kilo- ( used for just about anything, Europe uses x 103 K
the Kilometer instead of the mile on its roads)
Centi- ( Used significantly to express small x 10-2 c
distances in optics. This is the unit MOST people in
AP forget to convert)
Milli- ( Used sometimes to express small x 10-3 m
distances)
Micro- ( Used mostly in electronics to express the x 10-6
value of a charge or capacitor)
Nano ( Used to express the distance between x 10-9 n
wave crests when dealing with light and the
electromagnetic spectrum)
Tip: Use your constant sheet when you forget a prefix value

4. The importance of the metric system prefixes

5. Example
If a capacitor is labeled 2.5 F(microFarads),
how would it be labeled in just Farads?
The FARAD is the fundamental unit used when discussed capacitors!
Notice that we just add the factor on the
2.5 x 10-6 F end and use the root unit.
The radio station XL106.7 transmits at a
frequency of 106.7 x 106 Hertz. How would it
be written in MHz (MegaHertz)?
A HERTZ is the fundamental unit used when discussed radio frequency!
Notice we simply drop the factor and add
106.7 MHz the prefix.

6. SI: Derived Units
 units that come from multiplying or dividing fundamental units
Physical Quantity Unit Name Symbol
area square meter m2
volume cubic meter m3
meter per
speed m/s
second
meter per
acceleration m/s2
second squared
weight, force newton N (kg·m/s²)
energy, work joule J (N·m)

7. Dimensional Analysis
Dimensional Analysis is simply a technique you can use to convert from one unit
to another. The main thing you have to remember is that the GIVEN UNIT MUST
CANCEL OUT.
Suppose we want to convert 65 mph to ft/s or
m/s.
miles 1hour 1 min 5280 ft 65 1 1 5280 ft
65 1 60 60 1
95
hour 60 min 60 sec 1mile s
ft 1meter 95 1
29 m / s
95 3.281 ft 1 3.281
s

8. Trigonometric Functions
Many concepts in
physics act at angles
or make right triangles.
Let’s review common
functions.
c2 a2 b2
Pythagorean Theorem
-1 opp
tan ( )
adj

9. Example
A person attempts to measure the height of
a building by walking out a distance of
46.0 m from its base and shining a
flashlight beam toward its top. He finds
that when the beam is elevated at an
angle of 39 degrees with respect to the
horizontal ,as shown, the beam just
strikes the top of the building. a) Find
the height of the building and b) the
distance the flashlight beam has to
travel before it strikes the top of the
building.
What do I know? What do I Course of
want? action
•The angle The opposite USE
•The adjacent side side TANGENT!

10. Example
A truck driver moves up a straight mountain highway, as shown above.
Elevation markers at the beginning and ending points of the trip show that he
has risen vertically 0.530 km, and the mileage indicator on the truck shows
that he has traveled a total distance of 3.00 km during the ascent. Find the
angle of incline of the hill.
What do I know? What do I Course of
want? action
•The hypotenuse The Angle USE INVERSE
•The opposite side SINE!

11. Measurement & Precision
 The precision of a measurement depends on the
instrument used to measure it.
 For example, how long is this block?

12. Measurement & Precision
 Imagine you have a piece of string that is
exactly 1 foot long.
 Now imagine you were to use that string to
measure the length of your pencil. How
precise could you be about the length of the
pencil?
 Since the pencil is less than 1 foot, we must
be dealing with a fraction of a foot. But what
fraction can we reliably estimate as the length
of the pencil?

13. Measurement & Precision
 Suppose the pencil is slightly over half the 1 foot
string. You guess, “Well it must be about 7 inches,
so I’ll say 7/12 of a foot.”
 Here’s the problem: If you convert 7/12 to a
decimal, you get 0.583.
 Can you reliably say, without a doubt, that the pencil
is 0.583 and not 0.584 or 0.582?
 You can’t. The string didn’t allow you to distinguish
between those lengths… you didn’t have enough
precision.
 So, what can you estimate, reliably?

14. Measurement & Precision
 Basically, you have one degree of freedom… one
decimal place of freedom.
 So, the only fractions you can use are tenths!
 You can only reliably estimate that the pencil is 0.6 ft
long. It’s definitely more than 0.5 ft long and definitely
less than 0.7 ft long.
 Thus, precision determines the number of
significant figures we use to report measurements.
 In order to increase the precision of their
measurements, physicists develop more-advanced
instruments.

15. How big is the beetle?
Measure between the head
and the tail!
Between 1.5 and 1.6 in
Measured length: 1.54 in
The 1 and 5 are known with
certainty
The last digit (4) is estimated
between the two nearest fine
division marks.
Copyright © 1997-2005 by Fred Senese

16. Significant Figures
 Indicate precision of a measured value
 1100 vs. 1100.0
 Which is more precise? How can you tell?
 How precise is each number?
 Determining significant figures can be tricky.
 There are some very basic rules you need to
know. Most importantly, you need to practice!

17. Counting Significant Figures
The Digits Digits That Count Example # of Sig Figs
Non-zero digits ALL 4.337 4
Leading zeros
NONE 0.00065 2
(zeros at the BEGINNING)
Captive zeros
ALL 1.000023 7
(zeros BETWEEN non-zero digits)
ONLY IF they follow a
89.00 4
Trailing zeros significant figure AND
but
(zeros at the END) there is a decimal
8900 2
point in the number
0.003020 4
Leading, Captive AND Trailing Combine the
but
Zeros rules above
3020 3
Scientific Notation ALL 7.78 x 103 3

18. Calculating With Sig Figs
Type of Problem Example
3.35 x 4.669 mL = 15.571115 mL
MULTIPLICATION OR DIVISION:
rounded to 15.6 mL
Find the number that has the fewest sig
3.35 has only 3 significant figures, so
figs. That's how many sig figs should
that's how many should be in the
be in your answer.
answer. Round it off to 15.6 mL
64.25 cm + 5.333 cm = 69.583 cm
ADDITION OR SUBTRACTION:
rounded to 69.58 cm
Find the number that has the fewest
64.25 has only two digits to the right of
digits to the right of the decimal point.
the decimal, so that's how many
The answer must contain no more
should be to the right of the decimal
digits to the RIGHT of the decimal
in the answer. Drop the last digit so
point than the number in the problem.
the answer is 69.58 cm.

19. Scientific Notation
 Number expressed as:
 Product of a number between 1 and 10 AND a power of 10
 5.63 x 104, meaning
 5.63 x 10 x 10 x 10 x 10
 or 5.63 x 10,000
 ALWAYS has only ONE nonzero digit to the left of the
decimal point
 ONLY significant numbers are used in the first number
 First number can be positive or negative
 Power of 10 can be positive or negative

20. When to Use Scientific Notation
 Astronomically Large Numbers
 mass of planets, distance between stars
 Infinitesimally Small Numbers
 size of atoms, protons, electrons
 A number with “ambiguous” zeros
 59,000
 HOW PRECISE IS IT?

21. Order of Magnitude
 Approximation based on a number of
assumptions
 may need to modify assumptions if more precise
results are needed
 Order of magnitude is the power of 10 that
applies

22. Order of Magnitude – Process
 Estimate a number and express it in scientific notation
 The multiplier of the power of 10 needs to be between 1 and
10
 Divide the number by the power of 10
 Compare the remaining value to 3.162 ( 10 )
 If the remainder is less than 3.162, the order of magnitude is
the power of 10 in the scientific notation
 If the remainder is greater than 3.162, the order of magnitude
is one more than the power of 10 in the scientific notation
 Easier – Find the logarithm (base 10) of the number,
round it to the nearest whole number, and use that as
the power of 10

23. Using Order of Magnitude
 Estimating too high for one number is often
canceled by estimating too low for another
number
 The resulting order of magnitude is generally
reliable within about a factor of 10
 Working the problem allows you to drop
digits, make reasonable approximations and
simplify approximations
 With practice, your results will become better
and better

24. Uncertainty in Measurements
 There is uncertainty in every measurement –
this uncertainty carries over through the
calculations
 May be due to the apparatus, the experimenter,
and/or the number of measurements made
 Need a technique to account for this uncertainty
 We will use rules for significant figures to
approximate the uncertainty in results of
calculations

25. Percent Error
experimental - theoretical
% Error
theoretical
 Experimental  what you do in class (lab)
 Theoretical  what you look up in a book
(internet)

26. Percent Difference
( x1 x2 )
% Difference * 100
( x1 x2 ) 2
 x1 and x2 are two experimental values
 Percent difference is comparing two experimental values,
whereas percent error compares one experimental value with the
actual/accepted value.