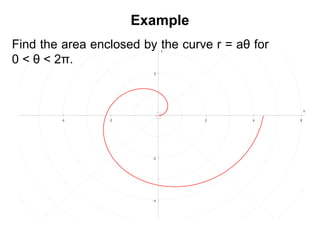
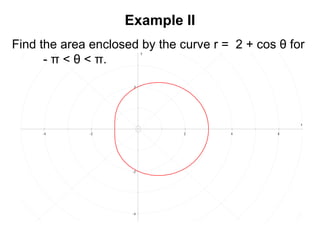
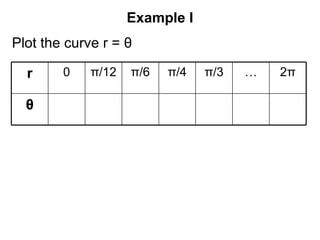
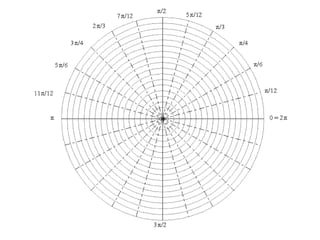
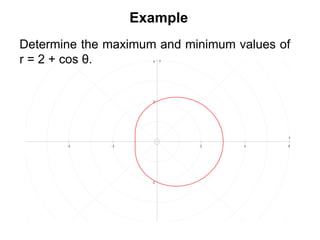
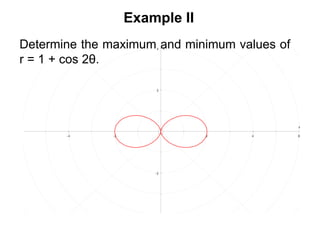
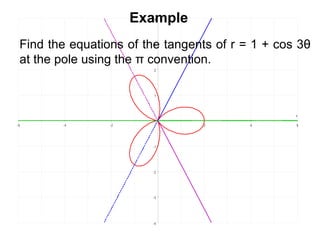
This document provides an overview of 8 lessons on polar coordinates. The lessons cover key concepts like plotting curves in polar form, converting between Cartesian and polar coordinates, determining maximum/minimum values of polar curves, and calculating areas bounded by polar curves. Example problems and practice questions are presented for each topic to help students learn the 'classic' polar curve shapes and how to work with polar coordinates.

1. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 1 -
Key Learning Points/Vocabulary:
● Plotting curves given in polar form.
● Investigating the shape of curves given in polar
form with a graphical calculator or computer.

2. Theory
An equation in polar form is given in the r = f(θ)
where θ is an angle measured anti-clockwise from
the origin/positive x-axis and r is the distance from
the origin.
e.g. If we are working with r = 2 + sin θ when θ = π/2,
r = 3.

3. Example I
Plot the curve r = θ
r 0 π/12 π/6 π/4 π/3 … 2π
θ

5. Example II
Plot the curve r = 2 sin(θ)
r 0 π/12 π/6 π/4 π/3 … 2π
θ

7. Practice
Construct tables showing value of θ between 0
and 2π in steps of π/12. Use these tables to
plot the following curves on polar paper.
• r = θ + sin (2θ)
• r = 2 + cos (θ)
• r = 3 sin (θ)
• r = 1 + sin (θ) + cos (θ)
• r = 1 + sin (θ) + cos (2θ)
• r = 2 + sin (θ) + cos (2θ)

8. Polar Co-ordinates
Experiment to learn the ‘classic’ curve shapes:
cos _( . ._ sin )
sin 2
(1 cos )
(1 2cos )
cos
sin cos
r a
r a c f r a
r a
r a
r a
r a
r a b
r a a
θ α
θ θ
θ
θ
θ
θ
θ
θ θ
=
=
= =
=
= +
= +
=
=
=

9. Polar Co-ordinates
Experiment to learn the ‘classic’ curve shapes:
cos _( . ._ sin )
sin 2
(1 cos )
(1 2cos )
cos
sin cos
r a
r a c f r a
r a
r a
r a
r a
r a b
r a a
θ α
θ θ
θ
θ
θ
θ
θ
θ θ
=
=
= =
=
= +
= +
=
=
=
Ray from origin
Circle, centred on the origin, radius a
Circle
Four-leafed clover
Cardioid
Limaçon
Spiral
Rose curve – see investigation
Lemniscate? Daisy

10. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 2 -
Key Learning Points/Vocabulary:
● Converting between Cartesian and Polar Co-
ordinates.

11. To start with …
Polar equations/graphs matching activity.

12. Theory
The 2π convention refers to when all angles are
given as a positive number between 0 and 2π e.g. all
angles are measured anti-clockwise from the
origin/positive x-axis.
The π convention refers to when all angles are
given as a positive or negative number between -π
and +π e.g. all angles are at most half a turn either
way from the origin/positive x-axis.

13. Examples
1.) Using a.) 2π and b.) π convention, express the
Cartesian point (3, -2) in polar form.
2.) Express the polar co-ordinate (2, 3π/4) in
Cartesian form.

14. Practice
1.) Using a.) 2π and b.) π convention, express the
Cartesian point (-2, -4) in polar form.
2.) Express the polar co-ordinate (3, -π/4) in
Cartesian form.
3.) Find the area of the triangle form by the origin and
the polar co-ordinates (2, π/4) and (4, 3π/8).
4.) FP2&3, page 96, questions 7 and 8.

15. Homework
See ‘Homework 1’ posted online.

16. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 3 -
Key Learning Points/Vocabulary:
● Polar co-ordinates and the use of symmetry.

17. - 4 - 2 2 4 6
- 2
2
4
x
y
r = 2 + cos θ
If f(θ) = f(-θ) for all values of θ, the graph with polar
equation r = f(θ) is symmetrical about the line θ = 0.

18. Theory
More generally if f(2α – θ) = f(θ) for all values of θ,
then graph with equations r = f(θ) is symmetrical
about the line θ = α.

19. Example
Plot the graph r = 2 sin 2θ for 0 ≤ θ ≤ π/2. Prove that
the graph is symmetrical about the line θ = π/4.

21. Practice
Further Pure Mathematics 2 and 3
Exercise 6C
Questions 1, 3 and 4

22. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 4 -
Key Learning Points/Vocabulary:
● Determining the maximum and minimum values of
curves given in Polar form.

23. Derivates from Core 4
Function Derivative
sin (ax) a cos (ax)
cos (ax) - a sin (ax)
tan (ax) a sec2
(ax)
sec (ax) a sec (ax) tan (ax)

24. - 4 - 2 2 4 6
- 2
2
4
x
y
Example
Determine the maximum and minimum values of
r = 2 + cos θ.

25. Example II
- 4 - 2 2 4 6
-2
2
4
x
yDetermine the maximum and minimum values of
r = 1 + cos 2θ.

26. Practice
Further Pure Mathematics 2 and 3
Exercise 6D
Questions 2 – part ii.) of each question only

27. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 5 -
Key Learning Points/Vocabulary:
● Finding the equations of tangents at the pole
(origin).

28. Theory
If f(α) = 0 but f(α) > 0 in an interval α < θ < … or
… < θ < α then the line θ = α is a tangent to the graph
r = f(θ) at the pole (origin)

29. - 6 - 4 - 2 2 4 6
- 4
- 3
- 2
- 1
1
2
3
4
x
yExample
Find the equations of the tangents of r = 1 + cos 3θ
at the pole using the π convention.

30. Practice
Further Pure Mathematics 2 and 3
Exercise 6D
Questions 2 – part iii.) of each question only

31. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 6 -
Key Learning Points/Vocabulary:
● Converting between Cartesian and Polar
Equations.

32. sin θ = y/r
→ y = r sin θ
cos θ = x/r
→ x = r cos θ
x2
+ y2
= r2
Theory

33. Examples
Convert the following equations into polar form:
i.) y = x2
ii.) (x2
+ y2
)2
= 4xy

34. Examples (continued)
Convert the following equations into Cartesian form:
iii.) r = 2a cos θ
iv.) r2
= a2
sin 2θ

35. Practice
Further Pure Mathematics 2 and 3
Exercise 6E
Questions 1 and 2

36. Homework
See ‘Homework 2’ posted online.

37. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 7 -
Key Learning Points/Vocabulary:
● Review of Double Angle Formulae from Core 3:
e.g. cos2
θ = … and sin2
θ = …
● Finding areas using Polar co-ordinates.

38. Integrals from Core 4
Function Derivative
sin (ax) - (1/a) . cos (ax)
cos (ax) (1/a) . sin (ax)
… see next slide for more detail …

39. [ ]
[ ]
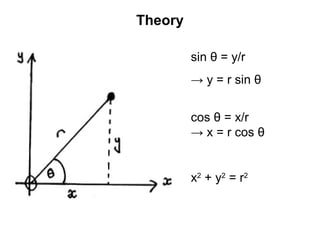
2
2
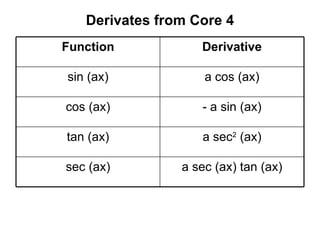
cos sin sin sin
sin cos cos cos
1
cos2 sin 2
2
1
cos 1 cos2
2
1
sin 1 cos2
2
bb
a a
bb
a a
b
b
a
a
b b
a a
b b
a a
d b a
d a b
d
d d
d d
θ θ θ
θ θ θ
θ θ θ
θ θ θ θ
θ θ θ θ
= = −
= − = −
 
=   
= +
= −
∫
∫
∫
∫ ∫
∫ ∫

40. Theory
The area of the region bounded by the graph r = f(θ)
and the radii θ = α and θ = β is given by
θθθ
β
α
β
α
dfdr 22
)]([
2
1
2
1
∫∫ =

41. Example
- 4 - 2 2 4 6
- 4
- 2
2
x
y
Find the area enclosed by the curve r = aθ for
0 < θ < 2π.

42. Example II
- 4 - 2 2 4 6
- 4
- 2
2
x
y
Find the area enclosed by the curve r = 2 + cos θ for
- π < θ < π.

43. Practice
Further Pure Mathematics 2 and 3
Exercise 6F
Questions 1 onwards

44. Homework
See ‘Homework 3’ posted online.

45. Further Pure Mathematics II
Polar Co-ordinates
- Lesson 8 -
Key Learning Points/Vocabulary:
● End of Topic Test based on FMN OCR FP2
materials.
● Learning Summary.
● Past Exam Questions.