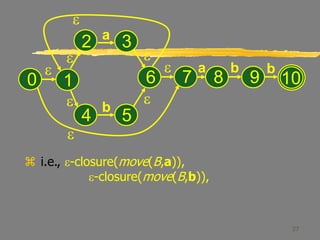
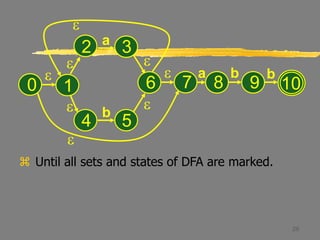
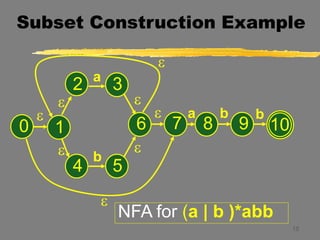
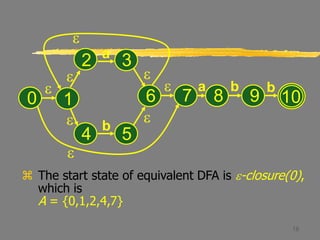
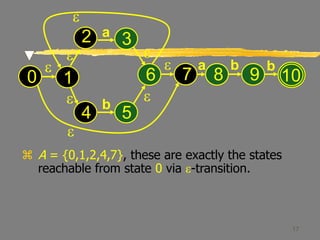
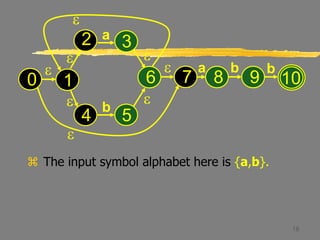
This document describes the process of converting a non-deterministic finite automaton (NFA) to a deterministic finite automaton (DFA) using subset construction. It provides examples to demonstrate how to determine the states and transitions of the equivalent DFA by tracking all possible states the NFA could be in after reading each input symbol. The key steps involve using e-closure and move operations on state sets to iteratively build up the DFA states and transition table until all states are determined.

1. 1
Theory Of Automata and
Formal languages (CS-536)
(Lecture 17)
______________________________________________________
GIMS- PMAS Arid Agriculture University, Gujrat Campus

2. 2
Kleene’s Theorem
 If a language can be expressed by
1. FA or
2. TG or
3. RE or
4. NFA/ NFA-epsilon
then it can also be expressed by other three
as well.

3. NFA to FA
Method as per discussed in class i.e. from the
notes
3

4. 4
NFA → DFA Construction
 The algorithm is called subset construction.
 In the transition table of an NFA, each entry is
a set of states.
 In DFA, each entry is a single state

5. 5
NFA → DFA Construction
The general idea behind
NFA-to-DFA construction is
that each DFA state
corresponds to a set of
NFA states.

6. 6
NFA → DFA Construction
The DFA uses its state to
keep track of all possible
states the NFA can be in
after reading each input
symbol.

7. 7
NFA → DFA Construction
We will use the following
operations.
e-closure(T):
set of NFA states reachable
from some NFA state s in T
on e-transitions alone.

8. 8
NFA  DFA Construction
move(T,a):
set of NFA states to which
there is a transition on input
a from some NFA state s in
set of states T.

9. 9
NFA → DFA Construction
Before it sees the first input
symbol, NFA can be in
any of the state in the set
e-closure(s0), where s0 is the
start state of the NFA.

10. 10
NFA → DFA Construction
Suppose that exactly the
states in set T are
reachable from s0 on a
given sequence of input
symbols.

11. 11
NFA → DFA Construction
Let a be the next input
symbol.
On seeing a, the NFA can
move to any of the states in
the set move(T,a).

12. 12
NFA → DFA Construction
When we allow for
e-transitions, NFA can be in
any of the states in
e-closure(move(T,a))
after seeing a.

13. 13
Subset Construction
Algorithm:
Input:
NFA N with state set S,
alphabet S, start state
s0, final states F

14. 14
Subset Construction
Output:
DFA D with state set
S’, alphabet S, start
states
s0’ = e-closure(s0),
final states F’,
transition
table: S’ x S → S’

15. 15
Subset Construction Example
NFA for (a | b )*abb
0
e
e
e e
e
a
b
e
e
1
2 3
4 5
6 8 9
e
7
a b b
10

16. 16
 The start state of equivalent DFA is e-closure(0),
which is
A = {0,1,2,4,7}
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

17. 17
 A = {0,1,2,4,7}, these are exactly the states
reachable from state 0 via e-transition.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

18. 18
 The input symbol alphabet here is {a,b}.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

19. 19
 The algorithm tells us to mark A and then
compute
e-closure(move(A,a))
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

20. 20
 move(A,a)), is the set of states of NFA that have
transition on ‘a’ from members of A.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

21. 21
 Only 2 and 7 have such transition, to 3 and 8.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

22. 22
 So, e-closure(move(A,a)) =
e-closure({3,8}) =
{1,2,3,4,6,7,8}
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

23. 23
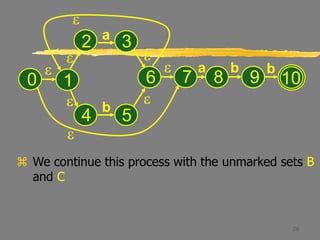
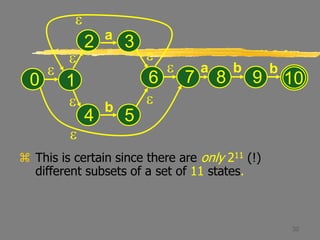
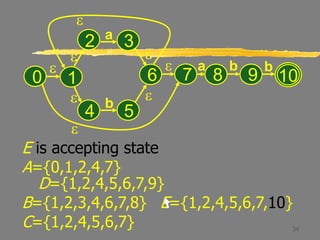
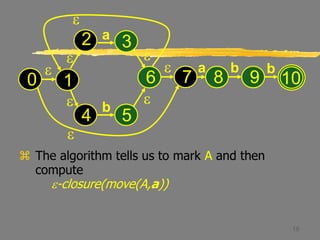
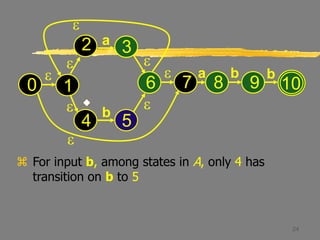
 Let B = {1,2,3,4,6,7,8}.
 Thus Dtran[A,a] = B
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

24. 24
 For input b, among states in A, only 4 has
transition on b to 5
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

25. 25
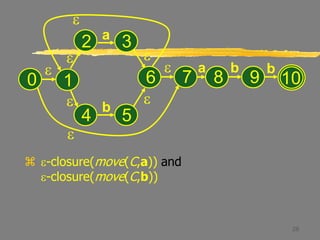
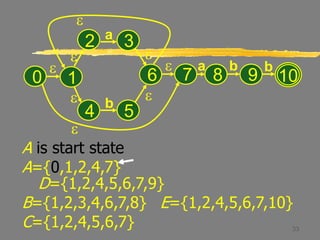
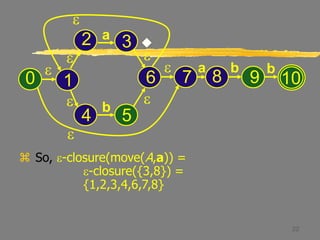
 C = e-closure({5})
= {1,2,4,5,6,7}
 Thus, Dtran[A,b] = C
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

26. 26
 We continue this process with the unmarked sets B
and C
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

27. 27
 i.e., e-closure(move(B,a)),
e-closure(move(B,b)),
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

28. 28
 e-closure(move(C,a)) and
e-closure(move(C,b))
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

29. 29
 Until all sets and states of DFA are marked.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

30. 30
 This is certain since there are only 211 (!)
different subsets of a set of 11 states.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

31. 31
 And a set, once marked, is marked forever.
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

32. 32
Eventually, the 5 sets are:
A={0,1,2,4,7}
B={1,2,3,4,6,7,8}
C={1,2,4,5,6,7}
D={1,2,4,5,6,7,9}
E={1,2,4,5,6,7,10}
Subset Construction

33. 33
A is start state
A={0,1,2,4,7}
D={1,2,4,5,6,7,9}
B={1,2,3,4,6,7,8} E={1,2,4,5,6,7,10}
C={1,2,4,5,6,7}
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

34. 34
E is accepting state
A={0,1,2,4,7}
D={1,2,4,5,6,7,9}
B={1,2,3,4,6,7,8} E={1,2,4,5,6,7,10}
C={1,2,4,5,6,7}
e
0
e
e
e e
e
a
b
e
1
2 3
4 5
6 8 9
e
7
a b b
10
e

35. 35
Resulting DFA
DFA for (a | b )*abb
A
a
b a
b b
E
B D
C
a
b
b
a
a

36. 36
Resulting DFA
A
a
b a
b b
E
B D
C
a
b
b
a
a
a a a
a b b

37. 37
Final Transition Table
State
Input symbol
a b
A B C
B B D
C B C
D B E
E B C