1) The document discusses synchronization techniques in operating systems, including semaphores invented by Dijkstra, which provide a way for processes to synchronize without busy waiting.
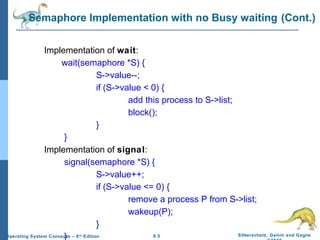
2) Semaphores use two operations - wait and signal - to synchronize access to shared resources. They can be implemented without busy waiting by blocking processes waiting on the semaphore.
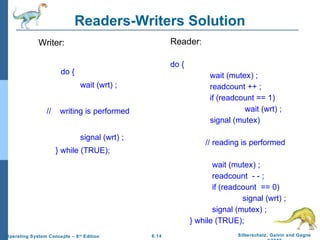
3) Classical synchronization problems like the bounded buffer, readers-writers problem, and dining philosophers problem are presented and solutions using semaphores are described to avoid deadlock and starvation.