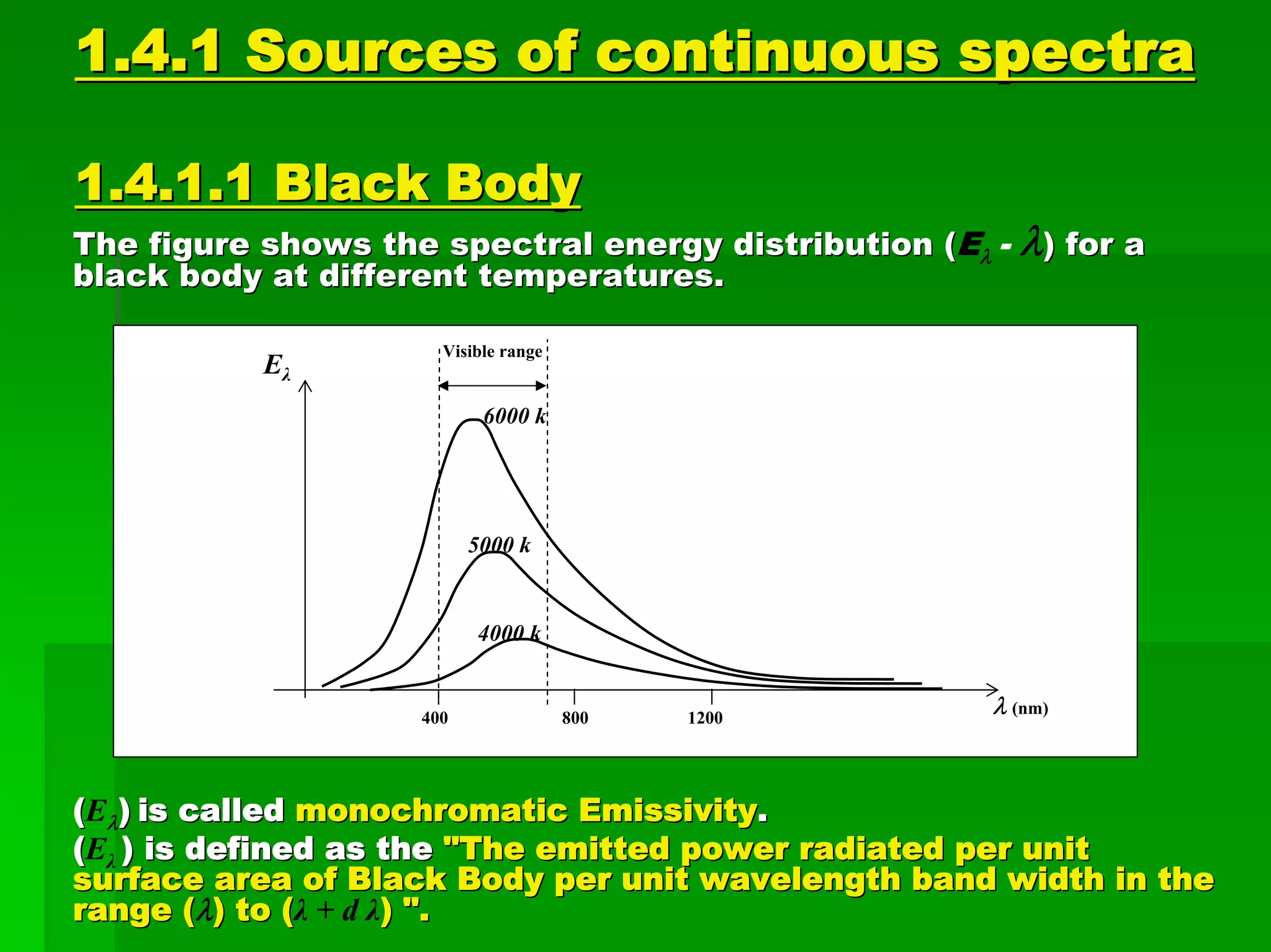
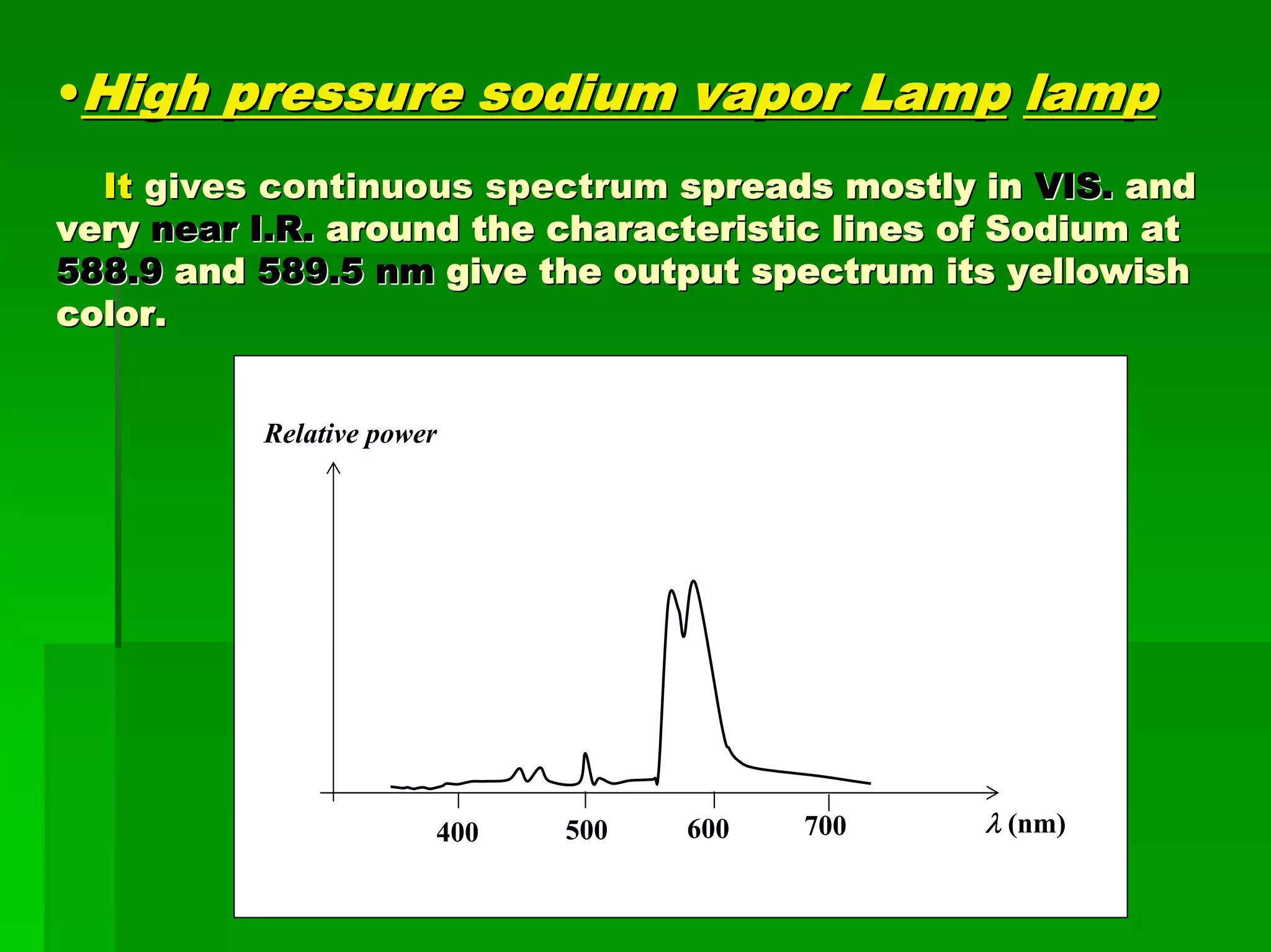
This document discusses optical analytical instrumentation and the interaction of electromagnetic (EM) radiation with matter. It describes different forms of spectra including absorption, emission, fluorescence, polarization, and scattering. A major class of analytical instruments is based on the interaction of radiation with matter, such as spectrophotometers, fluorometers, and polarimeters. The document then covers the nature of EM radiation as both waves and photons, properties of EM waves, sources of radiation including black bodies and gas discharge lamps, and the relationship between radiation, matter, and spectra.

1. OPTICAL ANALYTICALOPTICAL ANALYTICAL
INSTRUMENTATIONINSTRUMENTATION
Dr. Essam ElkaramanyDr. Essam Elkaramany

2. Interaction of EM Radiation withInteraction of EM Radiation with
MediaMedia
Different Forms of Spectra:Different Forms of Spectra:
AbsorptionAbsorption –– EmissionEmission-- FluorescenceFluorescence
PolarizationPolarization
ScatteringScattering
Rayleigh TypeRayleigh Type
Tyndal TypeTyndal Type
A major class of analytical instruments isA major class of analytical instruments is
based on the interaction of radiation withbased on the interaction of radiation with
mattermatter

3. ExamplesExamples::
SpectrophotometersSpectrophotometers
UV and Vis.UV and Vis.
IRIR
RamanRaman
SpectrofluorometersSpectrofluorometers
PolarimeterPolarimeter
TurbidimeterTurbidimeter –– NephelometerNephelometer
LASERLASER

4. CHAPTER ONECHAPTER ONE
PROPERTIES OFPROPERTIES OF
ELECTROMAGNETIC RADIATIONELECTROMAGNETIC RADIATION
ANDAND MATTERMATTER

5. 1.1 Nature of EM Radiation1.1 Nature of EM Radiation
EM RADIATIONEM RADIATION has double naturehas double nature
11-- WaveWave NatureNature
22-- QuantumQuantum (Particle)(Particle) NatureNature

6. 1.1.1 Wave1.1.1 Wave Nature ofNature of EM radiationEM radiation
the equationthe equation ::
Y = f( xY = f( x -- CtCt ))
Represents a disturbance with contourRepresents a disturbance with contour
yy=f(x)=f(x) at t=0, and is traveling in aat t=0, and is traveling in a
medium or in the space with constantmedium or in the space with constant
velocityvelocity CC in +ive xin +ive x--direction.direction.
Wave Velocity C
y =f(x)
y
x
at time=0 at time=t
y =f(x-Ct)

7. wave equationwave equation
2
2
2
2
2
x
f
C
t
f
∂
∂
=
∂
∂
Partial differential equation for waves traveling withPartial differential equation for waves traveling with
velocityvelocity CC in the x axis my be written as:in the x axis my be written as:
General Wave Equation:
fC
t
f 22
2
2
∇=
∂
∂

8. Harmonic (sinusoidal) wavesHarmonic (sinusoidal) waves
The general form of sinusoidal wave traveling in the positiveThe general form of sinusoidal wave traveling in the positive xx--axis is,axis is,
Y = Yo sin (Kx -wt + б)
Yo = The Amplitude
λ = The Wavlength
K = The wavenumber =
w = The angular velocity = 2πν
ν = The frequency
T = Periodic time =
Φ = The phase angle = (wt-Kx+ б)
C = Velocity of propagation = νλ =
2 π
Yo
бб
λ
π2
ν
1
k
w

9. EM WavesEM Waves
Direction of
propagation
•It consist of an electric field (E) and magnetic
field (B) are oscillating perpendicular to each
other and to the direction of propagation.
Equation of EM wave shown in the figure may be
written in terms of its electric field component,
i.e for EM wave propagated in z-direction:
E =E o sin (wt - Kz + б)

10. Properties of EM WavesProperties of EM Waves
A transverese waves which need no medium to
propagate and has its maximum speed Co in
vacuum, Co = 3X 108 m/s .
•• In any other medium, the speedIn any other medium, the speed CC is less thanis less than CCoo ,,
where,where,
((nn) is) is the refractive indexthe refractive index of the medium. It isof the medium. It is
characteristic of the medium and varies with thecharacteristic of the medium and varies with the
wavelength of the wave.wavelength of the wave.
For dielectric mediaFor dielectric media
n
C
Co
=
rεn =

11. ••The frequency (The frequency (ν) of a certain) of a certain EMEM wave remainswave remains
the same when traveling in different media whilethe same when traveling in different media while
its wavelength (its wavelength (λ) varies for different media, due) varies for different media, due
to variation of speed of propagation in theseto variation of speed of propagation in these
media according to the following relation:media according to the following relation:
where (where (λo) and () and (λm) are the values of the) are the values of the
wavelengths of the samewavelengths of the same EMEM wave in vacuumwave in vacuum
and any other medium of refractive index (and any other medium of refractive index (nn).).
n
C
C
(C/v)
/v)(C
λ
λ 0o
m
o
===

12. SPECTRUM OFSPECTRUM OF EMEM RADIATION:RADIATION:
RADIATION TYPE
Wavelength
(λ) nm
Frequency (v)
Hz
COSMIC RAYS 3x10-7-10-5 3xI022- I024
GAMMA RAYS 10-5-0.3 I018-3xl022
X-RAYS 3x10-4-30 l016-I021
ULTRA-
VIOLET
3 - 400 7.5xl014- l017
VISIBLE (Vis.) Violet-Red 400-700 4.28xl014-7.5xl014
INFRA RED
(I.R.)
NEAR 700-2500 1.2X10l4-4.28xl014
MEDIUM 2500-50000 6x10l2-1.2X10l4
FAR 50000-106 3X10ll-6x10l2
MICRO-WAVES 105 =1.0 m 3X108-3x1012
RADIO WAVES 1.0 m -103m 3x105-3x108

13. In PracticalIn Practical spectrophotometryspectrophotometry, we always use the, we always use the
range :range :
Infra red (IR)Infra red (IR)-- Visible (Vis)Visible (Vis)-- UltrvioletUltrviolet (UV)(UV)
IR : Near 700IR : Near 700 –– 2500 nm2500 nm
Med 2500Med 2500 –– 50000 nm50000 nm
Far 50000Far 50000 –– 101066
nmnm
Vis: 400Vis: 400 -- 700 nm700 nm
UV : 3UV : 3 -- 400 nm400 nm
700 nm630 nm590 nm560 nm482 nm440 nm400 nm
redorangeyellowgreenblueviolet

14. 1.1.2 Quantum1.1.2 Quantum Nature ofNature of EM radiationEM radiation
ByBy Plank'sPlank's Quantum TheoryQuantum Theory::
““ TheThe EMEM radiationradiation is not a continuous flowis not a continuous flow
of energy, but consists of discrete packetsof energy, but consists of discrete packets
of Energy", called "of Energy", called "PhotonsPhotons".".
The Energy (The Energy (ξξ) of each) of each PhotonPhoton, is, is
proportional to its frequency (proportional to its frequency (vv), and is), and is
given by the following formula:given by the following formula:
ξξ == hh νν
wherewhere ((hh)=)= 6.625 x 106.625 x 10--3434 joule.secjoule.sec = Planck's= Planck's
constant.constant.

15. ByBy Einstein'sEinstein's special theory ofspecial theory of
relativity :relativity :
Energy (Energy (ξξ) and matter (of mass) and matter (of mass mm), are), are
equivalentequivalent and are related by the followingand are related by the following
formula:formula:
ξ = m Co
2
accordingly the photon has the followingaccordingly the photon has the following
properties:properties:
* It has* It has zero rest masszero rest mass
* Its* Its mass at Cmass at Coo is given by:is given by:
m = ξ / Co
2 = h v / Co
2 = h /Co λ
*Its*Its momentummomentum is given by:is given by:
p = m Co = ξ /Co= h / λ

16. 1.2 Radiant Power (P):1.2 Radiant Power (P):
It is the radiant energy per unit time, i.e,It is the radiant energy per unit time, i.e,
P = dW /dt = d(Nξ)/dt
= ξ (dN/dt) = (hν) (dN/dt)
1.3 The Intensity of Radiation (1.3 The Intensity of Radiation (II))::
The Intensity of Radiation (The Intensity of Radiation ( II ) in any) in any
direction, is defined as the radiantdirection, is defined as the radiant
power per unit normal area in thatpower per unit normal area in that
direction, i.e,direction, i.e,
Watt/mWatt/m
A
P
I =

17. 1.4 SOURCES OF RADIATION:1.4 SOURCES OF RADIATION:
1.4.1 Sources of1.4.1 Sources of Continuous SpectrumContinuous Spectrum ::
11--Black Body (B.B.)Black Body (B.B.)
22--Tungsten LampTungsten Lamp
33-- Gas Filled Electric Discharge LampGas Filled Electric Discharge Lamp
** High Pressure Xenon lampHigh Pressure Xenon lamp
* High pressure Mercury vapor Lamp* High pressure Mercury vapor Lamp
* High pressure Sodium vapor Lamp* High pressure Sodium vapor Lamp
* Fluorescent Lamp* Fluorescent Lamp
1.4.2 Sources of1.4.2 Sources of Discontinuous SpectrumDiscontinuous Spectrum ::
11-- Gas Filled Electric Discharge LampGas Filled Electric Discharge Lamp
* Low pressure Mercury vapor Lamp* Low pressure Mercury vapor Lamp
* Low pressure Sodium vapor Lamp* Low pressure Sodium vapor Lamp
* Neon lamp* Neon lamp
22-- Hydrogen or Deuterium lampHydrogen or Deuterium lamp
33-- LEDLED
44-- LASER sourcesLASER sources

18. 1.4.1 Sources of continuous spectra1.4.1 Sources of continuous spectra
1.4.1.1 Black Body1.4.1.1 Black Body
The figure shows the spectral energy distribution (The figure shows the spectral energy distribution (Eλ - λ) for a) for a
black body at different temperatures.black body at different temperatures.
((Eλ)) is calledis called monochromatic Emissivitymonochromatic Emissivity..
((Eλ ) is defined as the) is defined as the "The emitted power radiated per unit"The emitted power radiated per unit
surface area of Black Body per unit wavelength band width in thesurface area of Black Body per unit wavelength band width in the
range (range (λ) to () to (λ + d λ) ".) ".
λ (nm)
Eλ
6000 k
5000 k
4000 k
400 800 1200
Visible range

19. From this definition, one can calculate theFrom this definition, one can calculate the
radiated power per unit surface area in the bandradiated power per unit surface area in the band
fromfrom λ1 toto λ2 as followsas follows
watt/m2watt/m2
LAWS OF BLACK BODY RADIATION:LAWS OF BLACK BODY RADIATION:
(1)(1) Stefan's lawStefan's law of total radiation:of total radiation:
λdEP
2
1
λ
λ
λ∫=
4
0
λT TσλdEP ==∫
∞

20. (2)(2) Wien'sWien's Displacement LawDisplacement Law::
λmax T = Constant = 2.93 x 10-3 m.oK
(3)(3) Planck's spectral energyPlanck's spectral energy ditributionditribution formulaformula::
It is deduced Theoretically by Planck, using hisIt is deduced Theoretically by Planck, using his
quantum hypothesisquantum hypothesis as follows,as follows,
where:where:
((C1C1) and () and (C2C2) are the first and second radiation) are the first and second radiation
constants.constants.
1e
λc
E /λλc
5
1
λ 2
−
=
−

21. 1.4.1.2 Tungsten Lamp:1.4.1.2 Tungsten Lamp:
ItIt IIs ans an incandescent lamp typeincandescent lamp type giving, when heated, radiationgiving, when heated, radiation
of continuous spectrum ranging betweenof continuous spectrum ranging between 320 to 3500 nm i.e.i.e.
consisting mainly ofconsisting mainly of VIS andand NEAR IR spectral regions.spectral regions.
It can be considered as aIt can be considered as a Gray body.Gray body.
i.e. may be approximated by black body radiation.i.e. may be approximated by black body radiation.
1.4.1.3 High pressure gas discharge Lamp:1.4.1.3 High pressure gas discharge Lamp:
Xenon lampXenon lamp
ItIt gives, when excited by suitable potential differencegives, when excited by suitable potential difference
between its electrodes, radiation of continuous spectrumbetween its electrodes, radiation of continuous spectrum
ranging betweenranging between 250 to 1000 nm i.e. consisting ofi.e. consisting of UV, VIS
andand NEAR IR spectral regions.spectral regions.

22. ••High pressure Mercury vapor LampHigh pressure Mercury vapor Lamp lamplamp
ItIt gives continuous spectrum withgives continuous spectrum with spikes showing thespikes showing the
characteristic lines of Mercury atcharacteristic lines of Mercury at 404.6, 407.7, 435.8, 491.6,404.6, 407.7, 435.8, 491.6,
546, 577 and 579 nm546, 577 and 579 nm. This gives the output spectrum its. This gives the output spectrum its
bluish color.bluish color.
λ(nm)
Relative power
500400 600 700

23. ••High pressure sodium vapor LampHigh pressure sodium vapor Lamp lamplamp
ItIt gives continuous spectrumgives continuous spectrum spreads mostly inspreads mostly in VIS.VIS. andand
veryvery near I.R.near I.R. around the characteristic lines of Sodium ataround the characteristic lines of Sodium at
588.9588.9 andand 589.5 nm589.5 nm give the output spectrum its yellowishgive the output spectrum its yellowish
color.color.
λ (nm)
Relative power
500400 600 700

24. 1.4.1.4 Fluorescent lamp1.4.1.4 Fluorescent lamp
It consists of a glass tube filled with Argon gas mixed withIt consists of a glass tube filled with Argon gas mixed with
evaporated Mercury atoms at low pressure. The tube suppliedevaporated Mercury atoms at low pressure. The tube supplied inin
each terminal with a pole from tungsten wire . The inner surfaceach terminal with a pole from tungsten wire . The inner surface ofe of
the tube is coated with fluorescent materialthe tube is coated with fluorescent material givininggivining whitewhite
spectrum mostly in the range from 300 nm to 700 nm .spectrum mostly in the range from 300 nm to 700 nm .
The figure shows the spectral energy distribution for theThe figure shows the spectral energy distribution for the
Daylight lamp type.Daylight lamp type.
λ (nm)
Relative power
500400 600 700

25. 1.4.2 Sources of1.4.2 Sources of Discontinuous SpectrumDiscontinuous Spectrum ::
1.4.2.11.4.2.1 Low Pressure Gas Filled ElectricLow Pressure Gas Filled Electric
Discharge LampDischarge Lamp::
**Low pressure Mercury vapor LampLow pressure Mercury vapor Lamp ::
which gives the spectrum shown in figure (bluishwhich gives the spectrum shown in figure (bluish –– green colors)green colors)
at characteristic lines of mercury.at characteristic lines of mercury.
λ (nm)
Relative power
500400 600 700

26. **Low pressure sodium vapor LampLow pressure sodium vapor Lamp ::
which gives the spectrum shown in figure (yellow color) atwhich gives the spectrum shown in figure (yellow color) at
characteristic lines of Sodium (588.9 and 589.5 nm)characteristic lines of Sodium (588.9 and 589.5 nm) ..
λ (nm)
Relative power
500400 600 700

27. **Neon lamp:Neon lamp:
gives characteristic line at 633 nm .gives characteristic line at 633 nm .
**Hydrogen or Deuterium lampHydrogen or Deuterium lamp::
It is used as a source of U.V. radiation (160 to 365 nm )It is used as a source of U.V. radiation (160 to 365 nm )
in the instruments of the spectral analysis due to itsin the instruments of the spectral analysis due to its
high intensity and its long live.high intensity and its long live.
1.4.2.2 LED1.4.2.2 LED
which is awhich is a PP--N junctionN junction
Silicon LED (1100 nm at near IR)Silicon LED (1100 nm at near IR)
GalliumGallium--Arsenide LED (Ga As) (900 nm at near I.R.)Arsenide LED (Ga As) (900 nm at near I.R.)
GalliumGallium--Phosphorus LED (700 nm)Phosphorus LED (700 nm)
GalliumGallium——Arsenide with phosphor coating (green 540 nm)Arsenide with phosphor coating (green 540 nm)

28. 1.4.2.3 LASER sources1.4.2.3 LASER sources
which are highly monochromatic, collimated and coherentwhich are highly monochromatic, collimated and coherent
sources.sources.
Examples of LASER sources are:Examples of LASER sources are:
Ruby LASER (693 nm).Ruby LASER (693 nm).
Argon LASER (515 nm).Argon LASER (515 nm).
HeliumHelium--Neon LASER (633 nm ).Neon LASER (633 nm ).
COCO22 LASER (Gaseous LASER) (10600 nm).LASER (Gaseous LASER) (10600 nm).

29. 1.7 METHODS OF1.7 METHODS OF
EXCITATION OF MATIER:EXCITATION OF MATIER:
(1)(1) Thermal excitationThermal excitation : by absorbing heat: by absorbing heat
energy.energy.
(2)(2) Electrical excitationElectrical excitation : by applying potential: by applying potential
difference or a strong electric field.difference or a strong electric field.
(3) Excitation by(3) Excitation by Electron BombardmentElectron Bombardment : a beam: a beam
of accelerated electrons is applied to atomsof accelerated electrons is applied to atoms
of matter to gain kinetic energy.of matter to gain kinetic energy.
(4) Excitation by(4) Excitation by IrradiationIrradiation : with a beam of: with a beam of
radiation of continuous spectrum from anradiation of continuous spectrum from an
external Sourceexternal Source