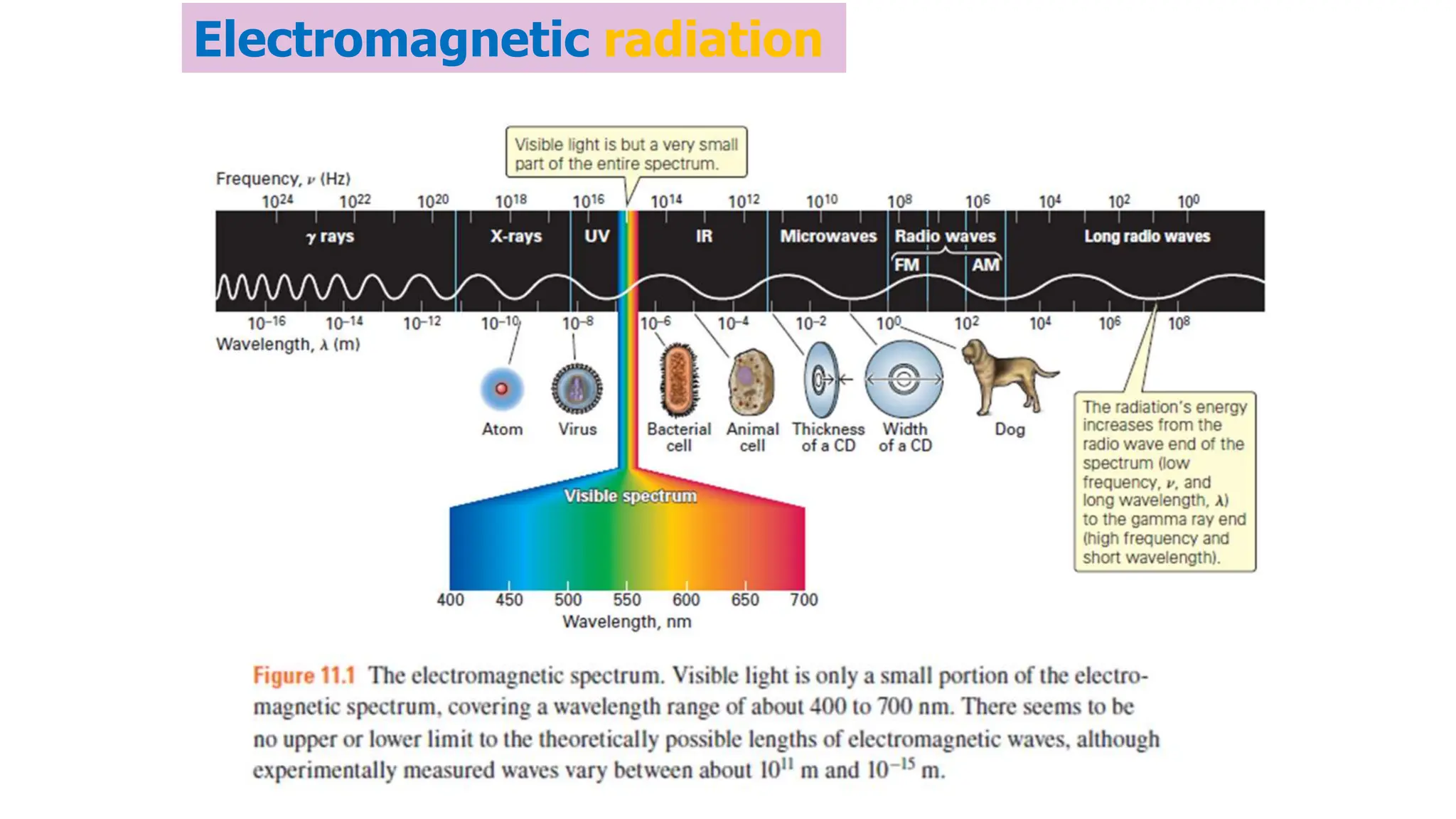
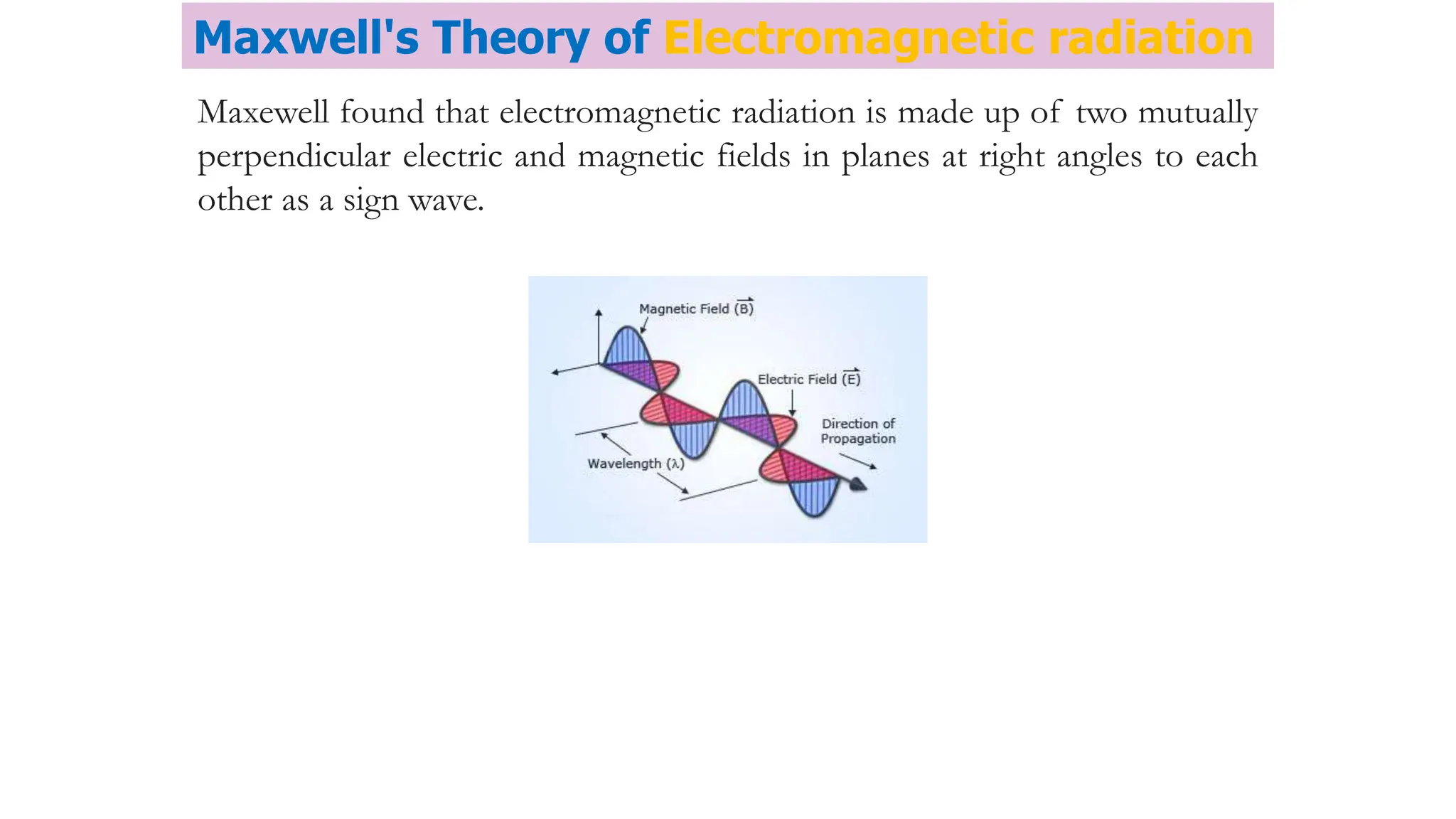
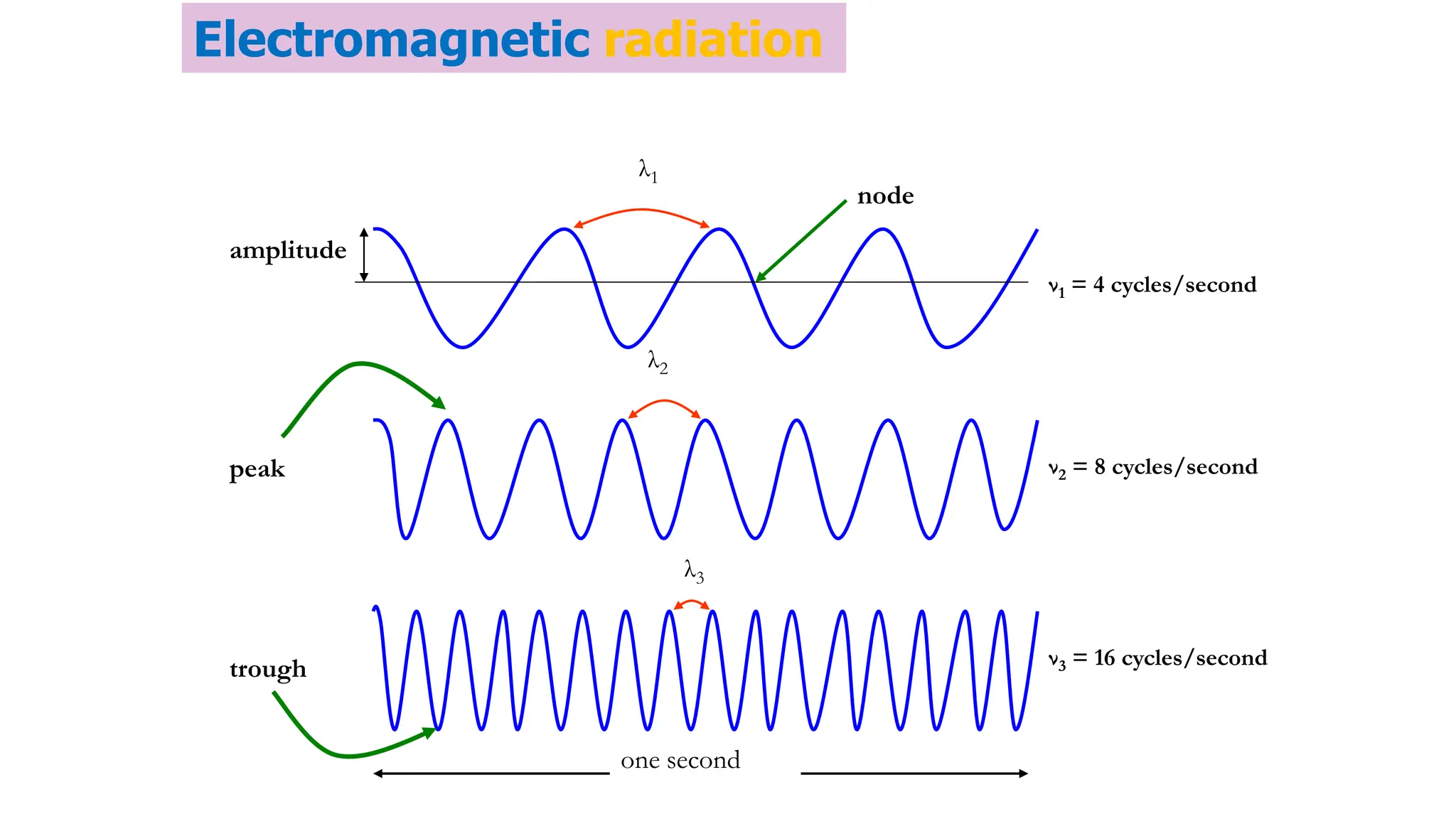
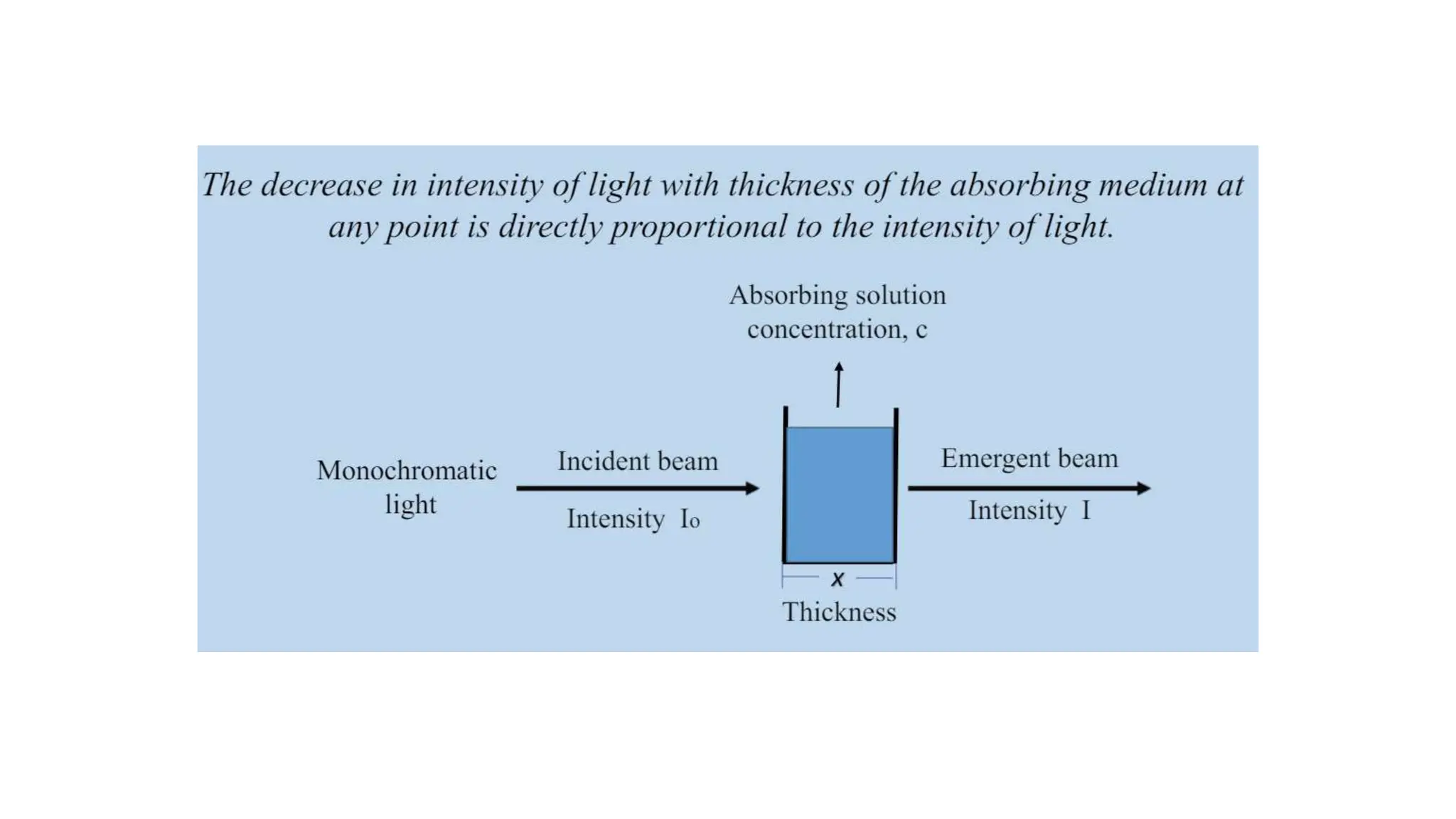
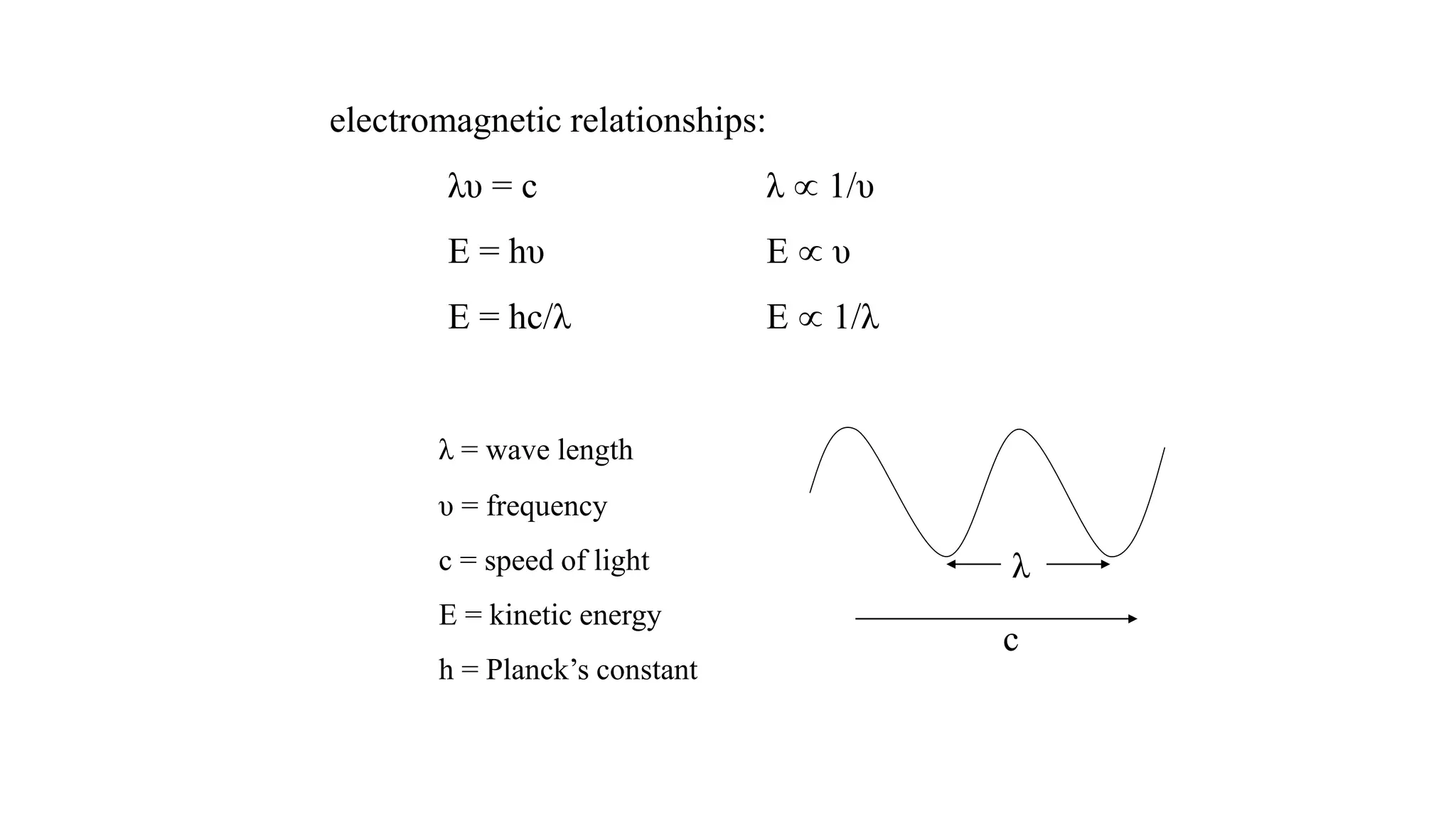
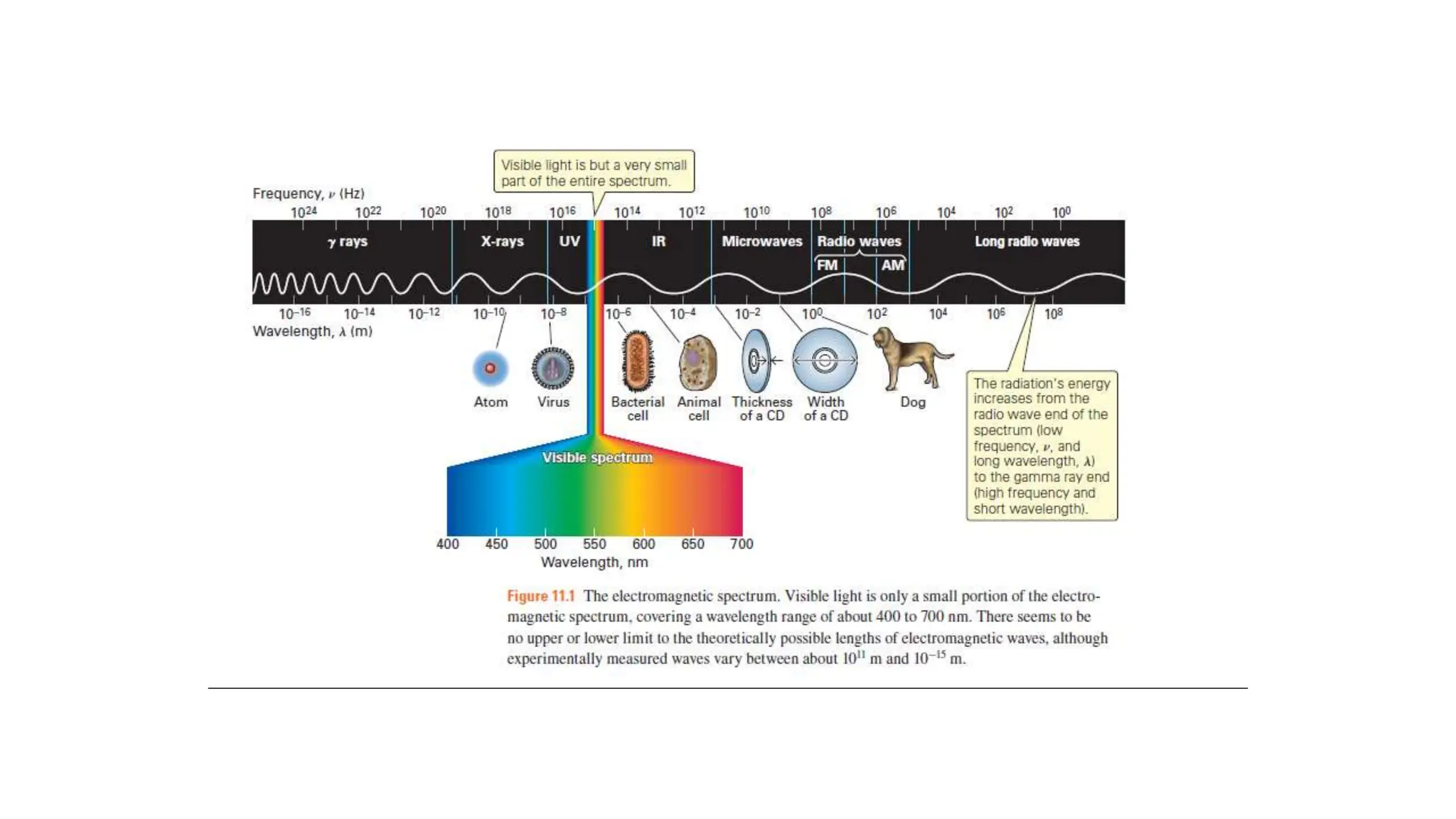
The document discusses electromagnetic radiation, detailing Maxwell's theory, the behavior of light, and key concepts such as wavelength, frequency, and the Beer-Lambert law, which relates light absorption to material properties. It explains how light can be polarized, monochromatic, or polychromatic, and outlines experimental methods for measuring light intensity and dispersion. Additionally, it addresses spectral line broadening and the relationship between molecular motion and spectroscopic techniques.

1. Spectroscopy
“Seeing the unseeable”

2. Electromagnetic radiation

3. Maxwell's Theory of Electromagnetic radiation
Maxewell found that electromagnetic radiation is made up of two mutually
perpendicular electric and magnetic fields in planes at right angles to each
other as a sign wave.

4. one second
λ1
λ3
λ2
ν1 = 4 cycles/second
ν2 = 8 cycles/second
ν3 = 16 cycles/second
amplitude
peak
trough
node
Electromagnetic radiation

5. Electromagnetic radiation can travel in vacuum. This velocity of light in
vacuum has a value
c = 2.997925 x 108 m s-1
 The distance between two peaks or two troughs is called the
wavelength and represented by λ (lambda).
 The product of the wavelength and the frequency (number of cycles per
second) is found to be c or
c = λν (1)
where ν is the frequency of the radiation. ν and λ are characteristic quantity of
the radiation for it is generally wavelength which is measured and always
frequency is more significant for the interpretation of spectra.
Electromagnetic radiation

6. Thus, spectral region may be presented in terms of

8. Wavelength (λ)
- Distance for a wave to go through a complete cycle (distance
between two consecutive peaks or troughs in a wave)
Frequency (ν)
- The number of waves (cycles) passing a given point in space per
second
Cycle
- Crest-to-crest or trough-to-trough
Speed (c)
- All waves travel at the speed of light in vacuum (3.00 x 108 m/s)
Electromagnetic radiation

9. Plane Polarized Light
- Light wave propagating along only one axis (confined to one plane)
Monochromatic Light
- Light of only one wavelength
Polychromatic Light
- Consists of more than one wavelength (white light)
Visible light
- The small portion of electromagnetic radiation to which the human
eye responds
Electromagnetic radiation

10. • Allow the monochromatic beam to fall on a detector, which will
measure its intensity
THE BASIC EXPERIMENT
• Take a white source of radiation
• Collimate the beam of radiation
• Place your sample in the path of radiation
• Disperse the transmitted beam of radiation
• Use a slit to isolate a monochromatic beam of radiation
• Scan through the range of frequencies to obtain data at a
reasonable number of frequencies
Collimated light is light whose rays are parallel

11. How is a beam of radiation dispersed ?
• By passing through a prism
• By reflection on a diffraction grating
How is a beam of radiation collimated ?
Place the source at the focus of
• A convex lens (glass or quartz for visible or uv radiation)
• A front silvered concave mirror for infrared radiation

12. Io
It
Sample
Absorbance = log (Io/It)
Transmittance (%) = (It/Io)x100
To measure Io, replace the sample with a reference, or use a dual
beam configuration
Definition of Transmittance and Absorbance
Spectrum is presented as a plot of
Absorbance or Transmittance vs frequency or wavelength

14. The Beer-Lambert Law, also known as Beer’s Law, relates the absorption of
light to the properties of the material through which the light is traveling. This
law is crucial in fields like chemistry and physics for understanding the
absorption characteristics of solutions. Let's derive the Beer-Lambert Law step
by step.
Assumptions :
1.Monochromatic Light: The light used has a single wavelength.
2.Homogeneous Medium: The absorbing medium is uniform in
concentration.
3.Straight Path: Light travels in a straight line through the medium.
4.No Scattering: Only absorption is considered; scattering is negligible.
Beer-Lambart Law
x
dx

16. Basic Concept
When a beam of light of intensity 𝐼0 enters an absorbing medium, its intensity
decreases exponentially with the distance traveled through the medium.
The decrease in intensity 𝑑𝐼 over a small distance 𝑑𝑥 is proportional to the
intensity of light 𝐼 and the concentration of the absorbing species 𝑐.
Mathematical Formulation
Differential Form:
here, x is the proportionality constant that depends on the nature of the
absorbing species and the wavelength of light.
Separation of Variables: Rearrange the differential equation:

17. Integration:
Integrate both sides of the equation. On the left side, integrate with respect
to 𝐼 from 𝐼0 (initial intensity) to 𝐼 (intensity after traveling distance 𝑥). On the
right side, integrate with respect to 𝑥 from 0 to 𝑥:

18. Spectral Line Broadening:
Line broadening is classified as either homogeneous, when all the atoms or
molecules experience the same effect, or inhomogeneous, in which each atom
or molecule is affected differently. In the former class comes natural line
broadening, while among the latter is Doppler broadening.

19. Pressure or collisional broadening
When collisions occur between gas phase molecules, their charge distribution is
disturbed, causing an induced dipole that can subsequently absorb or emit
radiation. This leads effectively to a broadening of energy levels.
If τ is the mean time between collisions, and each collision collision results in a
transition between two states, there is a line broadening Δv of the transition,
where
Δν = (2πτcoll)
according to the Uncertainty Principle. Like natural line broadening, this
broadening is homogeneous, and usually produces a Lorentzian line-shape
because of the similarity in the decay functions. However, for transitions at low
frequencies, the line-shape is unsymmetrical.
This kind of broadening increases with the pressure. The time between collisions
is related to the attraction between molecules; therefore, line-width investigations
are a common technique used to investigate intermolecular forces.

20. Translational motion of a molecule is the motion of the molecule
along arbitrarily defined x, y and z axes. The translational energy
of a molecule is only the kinetic energy.
Translational motion generally cannot be used by any
spectroscopic techniques, but it is important as part of the overall
motion of a molecule. Also, the kinetic energy - thus translational
energy - a molecule has can be lost by emission of a photon,
giving rise to emission spectra.

21. electromagnetic relationships:
λυ = c λ 1/υ
E = hυ E υ
E = hc/λ E 1/λ
λ = wave length
υ = frequency
c = speed of light
E = kinetic energy
h = Planck’s constant
λ
c

23. Spectroscopy
“seeing the unseeable”
Using electromagnetic radiation as a probe to obtain information
about atoms and molecules that are too small to see.
Electromagnetic radiation is propagated at the speed of light through
a vacuum as an oscillating wave.

24. Two oscillators will strongly interact when their energies
are equal.
E1 = E2
λ1 = λ2
υ1 = υ2
If the energies are different, they will not strongly interact!
We can use electromagnetic radiation to probe atoms and
molecules to find what energies they contain.

25. some electromagnetic radiation ranges
Approx. freq. range Approx. wavelengths
Hz (cycle/sec) meters
Radio waves 104 - 1012 3x104 - 3x10-4
Infrared (heat) 1011 - 3.8x1014 3x10-3 - 8x10-7
Visible light 3.8x1014 - 7.5x1014 8x10-7 - 4x10-7
Ultraviolet 7.5x1014 - 3x1017 4x10-7 - 10-9
X rays 3x1017 - 3x1019 10-9 - 10-11
Gamma rays > 3x1019 < 10-11