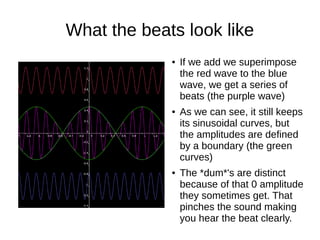
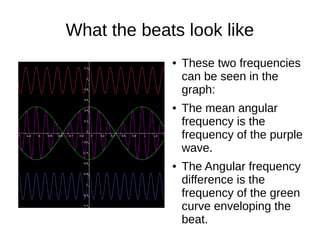
Beats occur when two sounds waves of similar frequencies interfere with each other. When the peaks of one wave align with the troughs of the other, they cancel each other out, creating a distinctive "dum" sound. This happens periodically as the waves go in and out of phase, producing the rhythm of beats. Beats can be visualized mathematically as a combination of two sinusoidal waves, with the amplitude defined by a boundary that creates the distinct pulses we hear. The frequency of these pulses is governed by both the mean angular frequency and the angular frequency difference between the original waves.

1. Beats
From High to Low and
Everything in Between

2. What are beats?
● When you listen to a song, there are some portions
where you can just hear a *dum dum dum* sound
(*wub wub wub* in other cases), and, more often than
not, we call those the beats of a song.
● 1 *dum*/*wub* = 1 beat
● But what are beats in the first place? And where do
they come from?

3. Learning Objectives
● Learn how beats are formed.
● Figure out what beats are: physically and
mathematically.
● Visualize why there would be a distinct *dum*
sound for beats

4. How are beats formed?
● If you have tried plucking two strings of a guitar that
are of different tones, you would have heard a faint
*wub wub* sound. Congratulations! You have just
made a beat!
● When two waves of close frequencies travel together I
the same direction, at any given time, there will be
places that are in-sync, constructively intefering with
each other, places that are out of sync, destructively
interfering with each other, and places in between.

5. !!!NOTE!!!
● The two waves need to be travelling at the same
direction and have the same amplitude in order to
form a beat.
● They need to have the same amplitude to make a
distinctive beat (one that pinches off to 0)
● They also need to be travelling in the same direction
to be observable. Imagine Listening for two sounds
one coming from the right (entering through the right
ear), and one from the left (entering from the left ear):
there wouldn't be physical interference happening.

6. What are beats physically?
● If we slowed down that beat, we would hear a
gradual increase from the beat's minimum
volume (intensity) to its max, then back to its
minimum, giving us one *dum*. It then repeats
to give us another beat, and so on.

7. What the beats look like
● If we add we superimpose
the red wave to the blue
wave, we get a series of
beats (the purple wave)
● As we can see, it still keeps
its sinusoidal curves, but
the amplitudes are defined
by a boundary (the green
curves)
● The *dum*'s are distinct
because of that 0 amplitude
they sometimes get. That
pinches the sound making
you hear the beat clearly.

8. Mathematically Speaking
st=sm(cos(k1x−ω1t)+cos(k2x−ω2t))
s2=smcos(k2 x−ω2 t)
α=k1 x−ω1 t
β=k2 x−ω2t
Let:
Thus a superposition of s1 and s2 would be:
s1=smcos(k1 x−ω1t)
The two waves in math form
st=sm(cosα+cosβ)
Using Angle Addition and Half-angle Identities:
st=2∗sm(cos
(α+β)
2
)(cos
(α−β)
2
)
Substituting back alpha and beta:
st=2∗sm(cos
(k1x−ω1t+k2x−ω2t)
2
)(cos
(k1x−ω1t−k2x−ω2t)
2
)
Factoring:
st=2∗sm(cos(
(k1+k2)x
2
−
(ω1+ω2)t
2
))(cos(
(k1−k2)x
2
−
(ω1−ω2)t
2
))
We can thus note that beats have
Two frequencies governing them:
Mean angular frequency:
ω=
(ω1+ω2)
2
Angular frequency difference:
Δ ω=
(ω1−ω2)
2

9. What the beats look like
● These two frequencies
can be seen in the
graph:
● The mean angular
frequency is the
frequency of the purple
wave.
● The Angular frequency
difference is the
frequency of the green
curve enveloping the
beat.

10. References:
● Hawkes, Iqbal, Mansour, Milner-Bolotin, & Williams. (2015). Interference and Sound. In Physics for Scientists
and Engineers Revised Custom (Vol. 1, pp. 249-250). Toronto: Nelson Education.
● Made by: Arnold Leigh Ryan Choa 32038144