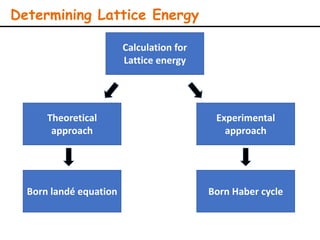
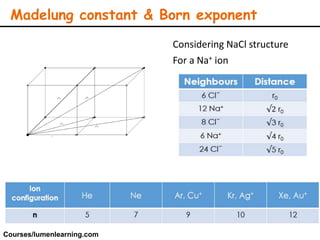
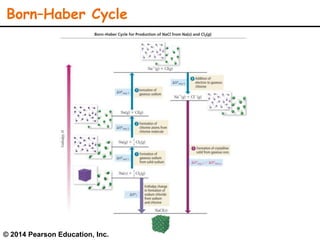
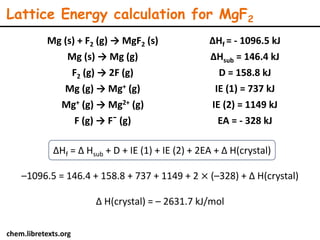
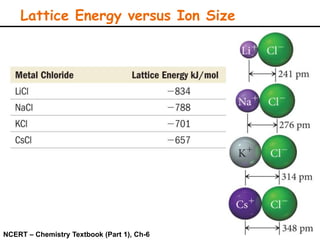
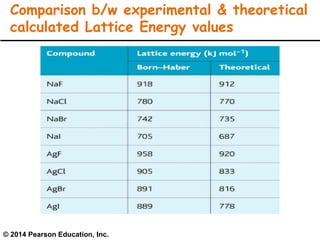
Lattice energy refers to the energy released when separate ions in the gas phase form an ionic crystal lattice. It can be calculated theoretically using the Born-Landé equation or experimentally using the Born-Haber cycle. The Born-Landé equation considers the electrostatic attraction and repulsive forces between ions, while the Born-Haber cycle uses standard enthalpy data and Hess's law. Lattice energy depends on factors like ion charge and size - higher charge or smaller ions lead to stronger electrostatic forces and higher lattice energy. Lattice energy is an important concept for understanding the properties and stability of ionic compounds.

1. Lattice energy
JNC 310 : Structure & Chemical Crystallography
Abhishek Rawat (S0750)
20 January 2020
N.C.U. - JNCASR

2. Outline
 Lattice energy & its properties
 Determination of lattice energy
 Lattice energy calculations
 Comparison b/w both approaches
 Q & A
 Conclusion

3. Where can lattice energy be valid?
Covalent Compounds Ionic Compounds
Lattice energies are associated with many interactions, as
cations and anions pack together in an extended lattice.
For covalent bonds, the bond dissociation energy is
associated with the interaction of just two atoms.
Metallic Compounds??

4. • Electrostatic attraction is
nondirectional!
– No direct anion–cation pair
• Therefore, there is no ionic
molecule
– The chemical formula is an
empirical formula, simply giving
the ratio of ions based on
charge balance
Crystal lattice of ionic compounds
© 2014 Pearson Education, Inc.

5. • I.E. of the metal is endothermic
Na(s) → Na+(g) + 1 e ─ DH° = +496 kJ/mol
• E.A. of the nonmetal is exothermic
½Cl2(g) + 1 e ─ → Cl─(g) DH° = −349 kJ/mol
• I.E. (metal) > E.A. (nonmetal)
• Formation of the ionic compound should be endothermic
• But the heat of formation of most ionic compounds is exothermic
and generally large. Why?
Na(s) + ½Cl2(g) → NaCl(s) DH°f = −787 kJ/mol
Energetics of ionic bond formation

6. • The extra stability that accompanies the formation of the crystal
lattice is measured as the lattice energy
• The lattice energy is the energy released when the solid crystal
forms from separate ions in the gas state
• Always exothermic
• Hard to measure directly, but can be calculated from knowledge
of other processes
• Lattice energy ∝ charge ∝ 1/ distance b/w ions
Lattice Energy
Courses/lumenlearning.com

7. • Melting/boiling point (stronger bonds = higher melting
point/boiling point)
• Hardness (stronger bonds = harder crystals)
• Odor (stronger bonds = weaker odor)
• State at room temperature (stronger bonds are more likely to be
solids)
• Solubility??
Properties of Lattice Energy

8. Determining Lattice Energy
Theoretical
approach
Experimental
approach
Born landé equation Born Haber cycle
Calculation for
Lattice energy

9. Born-Landé equation
In 1918, Max Born & Alfred Landé
proposed the formula for Lattice
energy calculation on the basis of
electrostatic potential of ionic lattice
and repulsive potential energy terms
𝑼 = −
𝑵 𝑨 𝑨 𝒛
+
𝒛
−
𝒆 𝟐
𝟒𝝅𝝐 𝟎 𝒓 𝟎
(𝟏 −
𝟏
𝒏
)
• NA = Avogadro no. = 𝟔. 𝟎𝟐𝟑 × 𝟏𝟎 𝟐𝟑
• A = Madelung const.
• z = Numeric charge of respective ion
• e = electronic charge = 𝟏. 𝟔 × 𝟏𝟎−𝟏𝟗
C
• 𝝐 𝟎 = permittivity of free space
(𝟒𝝅𝝐 𝟎 = 𝟏. 𝟏𝟏𝟐 × 𝟏𝟎−𝟏𝟎
C2/J.m)
• r0 = distance to closest ion
• n= Born exponent (approx. 5−12)
Courses/lumenlearning.com

10. Considering NaCl structure
For a Na+ ion
Madelung constant & Born exponent
Courses/lumenlearning.com

11.  Electrostatic potential
Epair = −
𝑧2
𝑒2
4𝜋𝜖0 𝑟
• z = magnitude of charge on each ion
• e = electronic charge = 1.6 × 10−19 C
• 𝜖0 = permittivity of free space
(4𝜋𝜖0 = 1.112 × 10−10 C2/J.m)
• r= distance between two oppositely
charged ions
EA = −
𝑧2
𝑒2
4𝜋𝜖0
𝑟
A
• A = Madelung constant, related to
geometry of the crystals.
 Repulsive potential
ER =
𝐵
𝑟 𝑛
• B = constant, scaling the strength of
the repulsive interaction
• r= distance between two oppositely
charged ions
• n= Born exponent (approx. 5−12),
expresses the steepness of the
repulsive barrier
Derivation of Born-Landé equation
Courses/lumenlearning.com

12. Total energy, U (r) = EA + ER
U (r) = −
𝑧2
𝑒2
4𝜋𝜖0
𝑟
𝐴 +
𝐵
𝑟 𝑛
Applying the minimization condition,
𝑑𝑈(𝑟)
𝑑𝑟
= 0, then r = r0
𝑑𝑈(𝑟)
𝑑𝑟
=
𝑧2 𝑒2
4𝜋𝜖0 𝑟0
2
𝐴 −
𝑛𝐵
𝑟0
𝑛+1
= 0
r0= (
4𝜋𝜖0
𝑛𝐵
𝑧2
𝑒2
𝐴
)
1
𝑛−1
𝐵 =
𝑧2
𝑒2
𝐴
4𝜋𝜖0
𝑛
𝑟0
𝑛−1
𝑈(𝑟0) = −
𝐴𝑧2 𝑒2
4𝜋𝜖0 𝑟0
(1 −
1
𝑛
)
Derivation of Born-Landé equation
Courses/lumenlearning.com

13. Drawbacks of Born-Landé equation
Calculations for lattice energy was based on Coulomb’s law
which considers ions as point charges
In deriving lattice energy the reduction of charges due to their
interactions are not considered
Courses/lumenlearning.com

14. Modification of Born-Landé equation
Born-Mayer equation
Mayer showed that e–r/ρ , where ρ is a constant dependent on
the compressibility of the crystal, gives a better repulsion term
than
1
𝑟 𝑛
𝑈 𝐵𝑀 = −
𝑁 𝐴 𝐴 𝑧
+
𝑧
−
𝑒2
4𝜋𝜖0 𝑟0
(1 −
𝜌
𝑟0
)
ρ = 30 pm works well for all alkali metal halides and other
simple cases when r0 values are in pm.
Courses/lumenlearning.com

15. Modification of Born-Landé equation
In the absence of detailed structural data, Kapustinskii's
equation can be used to estimate U
𝑈 𝐾 = 𝐾
𝑣𝑧
+
𝑧
−
𝑟++ 𝑟− (1−
𝑑
𝑟++ 𝑟−)
K = 1.202 × 10−4 𝐽. 𝑚/𝑚𝑜𝑙
𝑑 = 3.45 × 10−11 𝑚
𝑣 = no. of ions in the emperical formula
r = ionic radii of ions, in meter
Kapustinskii’s equation
Courses/lumenlearning.com

16. • Gives a good estimation. Real value differs in most cases by less than
5%
• Used with ionic compounds containing polyatomic ions as a means of
calculating their thermochemical radii, in which the ions are treated
as spheres
• Useful for complex ions like sulfate (SO4
2−) or phosphate (PO4
3−)
Advantages of Kapustinskii’s equation
Courses/lumenlearning.com

17. Experimentally determining Lattice Energy
• The Born–Haber cycle is a hypothetical series of reactions
that represents the formation of an ionic compound from its
constituent elements
• The reactions are chosen so that the change in enthalpy of
each reaction is known except for the last one, which is the
lattice energy
NCERT – Chemistry Textbook (Part 1), Ch-6

18. Born–Haber Cycle
• Use Hess’s law to add up enthalpy changes of other reactions to
determine the lattice energy
 DH°f(salt) = DH°f(metal atoms, g) + DH°f(nonmetal atoms, g)
+ DH°f(cations, g) + DH°f(anions, g) + DH°(crystal lattice)
 DH°(crystal lattice) = lattice energy
 For metal atom(g)  cation(g), DH°f = first ionization energy
 Add together all the ionization energies to get to the desired cation
M2+ = 1st IE + 2nd IE
 For nonmetal atoms (g)  anions (g), DH°f = electron affinity
NCERT – Chemistry Textbook (Part 1), Ch-6

19. © 2014 Pearson Education, Inc.
Born–Haber Cycle

20. According to Hess’s law, total energy change during the
complete course of a chemical reaction is the same whether
the reaction is made in one step or multi steps.
ΔHf = Δ Hsub + 1
2 𝐷 + IE + EA + Δ H(crystal)
Na (s) +
𝟏
𝟐
Cl2 (g) → NaCl (s)
ΔHf = - 410.9 kJ
Na (s) → Na (g) ΔHsub = 107.7 kJ
Cl2 (g) → 2Cl (g) D = 243.4 kJ
Na (g) → Na+ (g) IE = 496 kJ
Cl (g) → Clˉ (g) EA = - 349 kJ
Lattice Energy calculation for NaCl
chem.libretexts.org

21. Mg (s) + F2 (g) → MgF2 (s) ΔHf = - 1096.5 kJ
Mg (s) → Mg (g) ΔHsub = 146.4 kJ
F2 (g) → 2F (g) D = 158.8 kJ
Mg (g) → Mg+ (g) IE (1) = 737 kJ
Mg+ (g) → Mg2+ (g) IE (2) = 1149 kJ
F (g) → Fˉ (g) EA = - 328 kJ
–1096.5 = 146.4 + 158.8 + 737 + 1149 + 2 × (–328) + Δ H(crystal)
Δ H(crystal) = – 2631.7 kJ/mol
Lattice Energy calculation for MgF2
chem.libretexts.org
ΔHf = Δ Hsub + D + IE (1) + IE (2) + 2EA + Δ H(crystal)

22. Trends in Lattice Energy: Ion Charge
• The force of attraction between oppositely
charged particles is directly proportional to
the product of the charges
• Larger charge means the ions are more
strongly attracted
– Larger charge = stronger attraction
– Stronger attraction = larger lattice
energy
• Of the two factors, ion charge is generally
more important
NCERT – Chemistry Textbook (Part 1), Ch-6

23. Lattice Energy versus Ion Size
NCERT – Chemistry Textbook (Part 1), Ch-6

24. © 2014 Pearson Education, Inc.
Comparison b/w experimental & theoretical
calculated Lattice Energy values

25. Which compound will have the greatest lattice energy,
MgS or LiF?
• Magnitude of charge is the first thing we should look at
– magnesium (2+ charge), sulfide (2- charge)
– lithium (1+ charge), fluoride (1- charge)
– MgS has the greater individual charges, so MgS has the
greater lattice energy.
Q & A

26. Which compound will have lower melting point,
Na2S or BeO?
• A lower melting point means we need to select the compound
with the lower lattice energy. We check the charges first.
– sodium (1+), sulfide (2-)
– beryllium (2+), oxide (2-)
– sodium sulfide has smaller individual charges, so it has the
lower melting point.
Q & A

27. Which compound has harder crystals, CaCl2 or MgCl2?
• Harder crystals require a higher lattice energy. First, check the
charges.
– calcium (2+), chloride (1-)
– magnesium (2+), chloride (1-)
– the charges are the same, so we need to see which ions
have fewer energy levels.
Q & A

28. Which compound has harder crystals, CaCl2 or MgCl2?
– the charges are the same, so we need to see which ions
have fewer energy levels.
– calcium (4), chloride (3)
– magnesium (3), chloride (3)
– fewer energy levels give MgCl2 the higher lattice energy
and therefore, the harder crystals.
Q & A

29. Which compound has the lower boiling point,
AgNO3 or K2SO4?
• Lower boiling point means a lower lattice energy.
– silver (1+), nitrate (1-)
– potassium (1+), sulfate (2-)
– Charges indicate a lower lattice energy for AgNO3. Lower
lattice energy means a lower boiling point.
Q & A

30. Conclusion
We have learnt
• Lattice energy & its significance
• Approaches to determine it
• Modification of the theoretical approaches
• Experimental calculation
• Trends in lattice energy determination

31. Thank you

32. Assignment
Q1. Will lattice energy concept be valid for metallic
compounds? Why or Why not?
Q2. Assume the interionic distance for NaCl2 to be the same
as those of NaCl (r = 282 pm), and assume the structure to be
of the fluorite type (M = 2.512). Evaluate the energy of
crystallization, Ecryst .