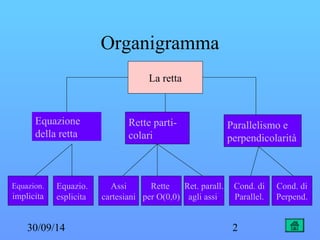
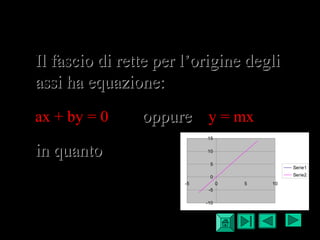
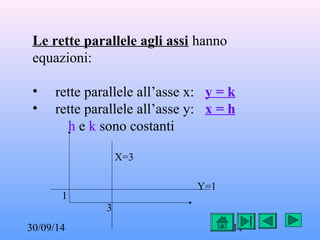
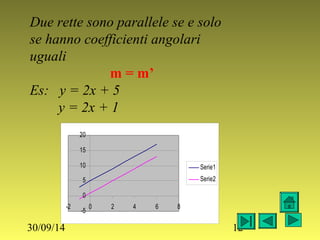
Il documento descrive la funzione lineare e le equazioni delle rette nel piano cartesiano, analizzando il parallelismo e la perpendicolarità. Viene presentata l'equazione implicita e esplicita della retta e le condizioni per determinare se due rette sono parallele o perpendicolari. Si evidenziano anche le equazioni delle rette parallele agli assi e delle rette particolari, come gli assi cartesiani.