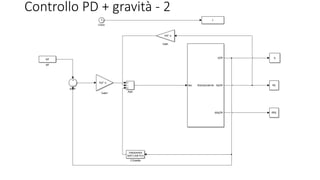
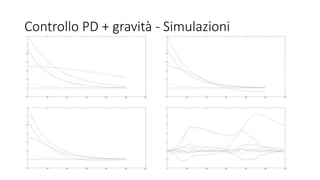
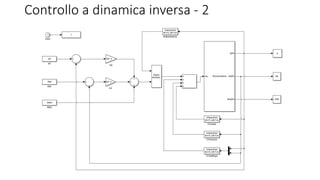
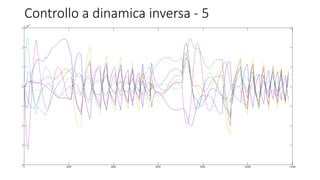
Il documento presenta un progetto su un manipolatore robotico SMARSix della Comau, analizzando la cinematica diretta e differenziale, oltre alla pianificazione della traiettoria e controllo del sistema. Utilizzando MATLAB e l'ambiente di simulazione V-REP, sono stati sviluppati algoritmi per l'inversione cinematica e il controllo delle traiettorie. I risultati delle simulazioni sono stati confrontati con le teorie, confermando la congruenza dei dati con l'implementazione pratica.

1. Università degli studi di Salerno
Corso di Laurea Magistrale in Ingegneria Informatica
Anno 2015/2016
Corso di Automazione e Robotica
Presentazione progetto Robotica
Gruppo: Di Gruttola Carmine – Esposito Emiddio

2. Outline
1. Analisi del manipolatore
2. Cinematica diretta del manipolatore
3. Cinematica differenziale, Inversione cinematica e pianificazione
della traiettoria
4. Controllo centralizzato nello spazio giunti

3. Strumenti utilizzati
• Matlab versione r2015a per lo sviluppo delle procedure.
• Ambiente di simulazione V-REP.

4. Analisi
• Il manipolatore analizzato è lo SmartSix della Comau poggiato su una
base mobile e con un polso sferico all’estremità.
• Il sistema risulta quindi composto da 6 giunti rotoidali disposti su
diversi assi.
• La base mobile è stata modellata aggiungendo due giunti prismatici,
idealmente posti nello stesso punto del primo giunto rotoidale.

5. Utilizzando le convenzioni di
Denavit-Hartenberg, sono state
individuate le terne solidali ai
diversi giunti

6. Dalle terne individuate e dal
datasheet sono stati estratti i
parametri DH che permettono
in maniera agevole di ricavare
le matrici di rotazione
Transizione a 𝜶 d 𝜽
𝑇𝑒𝑟𝑛𝑎 0 → 𝑇𝑒𝑟𝑛𝑎 1 0
𝜋
2
𝑞1
𝜋
2
𝑇𝑒𝑟𝑛𝑎 1 → 𝑇𝑒𝑟𝑛𝑎 2 0
𝜋
2
𝑞2
𝜋
2
𝑇𝑒𝑟𝑛𝑎 2 → 𝑇𝑒𝑟𝑛𝑎 3 0.15 −
𝜋
2
0.45 𝑞3
𝑇𝑒𝑟𝑛𝑎 3 → 𝑇𝑒𝑟𝑛𝑎 4 0.59 0 0 𝑞4
𝑇𝑒𝑟𝑛𝑎 4 → 𝑇𝑒𝑟𝑛𝑎 5 0.13 −
𝜋
2
0 𝑞5
𝑇𝑒𝑟𝑛𝑎 5 → 𝑇𝑒𝑟𝑛𝑎 6 0
𝜋
2
0.64707 𝑞6
𝑇𝑒𝑟𝑛𝑎 6 → 𝑇𝑒𝑟𝑛𝑎 7 0 −
𝜋
2
0 𝑞7
𝑇𝑒𝑟𝑛𝑎 7 → 𝑇𝑒𝑟𝑛𝑎 8 0 0 0.095 𝑞8

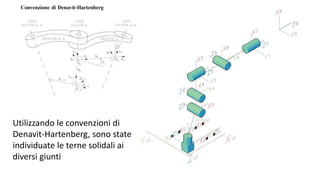
7. Cinematica Diretta
• Il primo passo è stato lo sviluppo di una procedura per il calcolo della
cinematica diretta.
• La procedura prende in ingresso la configurazione dei giunti del
manipolatore, una stringa per la tipologia degli angoli di Eulero e le
matrici 𝐴0
𝑏
e 𝐴 𝑒
𝑛
di relazione con la terna mondo e quella end effector
• In uscita restuisce la posizione dell’end effector, l’orientamento
secondo gli angoli scelti, la matrice di rotazione 𝑅 𝑒
𝑏 e un cell array con
tutte le matrici intermedie calcolate.
function [p, phi, R, A] = cindir(q, str, Ab0, Ane)

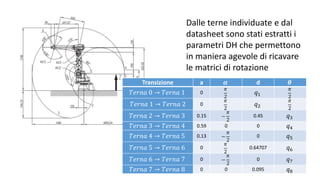
8. Procedura DHMatrix
• Per aiuto nello sviluppo, è stava sviluppata una procedura che dati i
parametri DH calcola la matrice di rototraslazione corrispondente.
• La stessa poi è stata utilizzata più volte per calcolare 𝐴 𝑒
𝑏, da cui sono
stati ricavate tutte le altre informazioni ritornate da cindir.
function [A] = DHMatrix(a, alpha, d, theta)

9. Verifica
• Confronto dei risultati in uscita dalla procedura realizzata con quelli
simulati dall’ambiente V-REP.
• In primo luogo sono stati verificati i risultati in posizione di
calibrazione, ovvero [0,0,0,−
𝜋
2
,0,0,0,0]T e i valori sono congruenti.
• Un’ulteriore prova è stata fatta in una posizione casuale
[5,5,0,0,−
𝜋
2
,0,0,0]T e si è notata una discrepanza di 0.06 mm nella
coordinata z della posizione causata dai limiti fisici dei giunti, nel caso
particolare dal giunto 5.
• Questo problema è stato risolto utilizzando il file
LimitiManipolatore.m

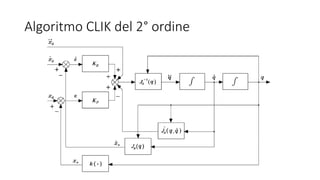
10. Inversione Cinematica
• Secondo passo è stato il calcolo della cinematica differenziale ai fini
dell’inversione cinematica, implementata attraverso un algoritmo CLIK
del secondo ordine
• La funzione prende in ingresso una configurazione iniziale, una
traiettoria in posizione, velocità e accelerazione, oltre che
informazioni su eventuali ostacoli.
function [q, dq, ddq, e] =
InversioneCinematica(q0, xd, dxd, ddxd, str, Ab0, Ane, obs)

11. Jacobiano Geometrico e Analitico
• Per l’inversione il primo passo è il calcolo dello Jacobiano Geometrico
𝐽 𝑞 e dello Jacobiano Analitico 𝐽 𝐴(𝑞)
• Il primo è stato calcolato a partire dalle formule presenti sul testo e
dalle informazioni ricavate da cindir
• Il secondo è stato calcolato partendo dal primo e utilizzando la
matrice di trasformazione ω = T Φ Φ, per ricavare Φ partendo da
ω.

12. Algoritmo CLIK del 2° ordine

13. Algoritmo CLIK del 2° ordine
• Utilizzato per compensare l’errore di integrazione in Eulero in avanti.
• Due costanti di retroazione, 𝐾 𝑑 e 𝐾𝑝 scelte uguali per dare un tempo
di assestamento di 50 ms senza oscillazioni, ovvero 𝜔 𝑛 = 100 e 𝜁 = 1
• Proiezione nel nullo per allontanarsi da ostacoli (supposti fermi e
cilindrici) e dai limiti di giunti
𝑞0 = 𝑞0 − 𝑞
𝑞0𝑖 = −𝑘1
𝑞 𝑖−𝑞 𝑚
𝑞 𝑖𝑀− 𝑞 𝑖𝑚
𝑞0𝑖 = 2𝑘2 𝑞𝑖 − 𝑜𝑖
• 𝑘1 e 𝑘2 sono stati fissati a 100 e 10 dopo prove sperimentali

14. Traiettoria - 1
• Traiettoria per operazione di pick and place
• Divisa in due sottotraiettorie:
• Dalla posizione di calibrazione alla posizione di pick
• Dalla posizione di pick alla posizione di place
• Percorso calcolato con ascissa curvilinea con archi di circonferenza
𝛾𝑝 = 𝑐 + 𝑅 ∗
𝑟 ∗ cos(
𝑠
𝑟
)
𝑟 ∗ sin(
𝑠
𝑟
)
0
𝛾𝑓 = 𝑓0 + 𝑠 ∗
𝑓 𝑓−𝑓0
𝐿
• Punto di via calcolato per passare lontano dagli ostacoli

15. Traiettoria - 2
Vista laterale
Vista dall’alto

16. Traiettoria - 3
• Per l’ascissa curvilinea è stata scelto un profilo trapezoidale con
due secondi in aggiunta, per simulare le operazioni di pick e place
• 𝑠(𝑡) =
𝑎 𝑚𝑎𝑥 ∗
𝑡2
2
𝑐𝑜𝑛 𝑡 < 𝑡 𝑐
𝑣 𝑚𝑎𝑥 ∗ 𝑡 −
𝑣 𝑚𝑎𝑥
2
2∗𝑎 𝑚𝑎𝑥
𝑐𝑜𝑛 𝑡 𝑐 < 𝑡 < 𝑡𝑓 − 𝑡 𝑐
−𝑎 𝑚𝑎𝑥 ∗
𝑡−𝑡 𝑓
2
2
+ 𝑣 𝑚𝑎𝑥 ∗ 𝑡𝑓 −
𝑣 𝑚𝑎𝑥
2
𝑎 𝑚𝑎𝑥
𝑐𝑜𝑛 𝑡𝑓 − 𝑡 𝑐 < 𝑡 < 𝑡𝑓
𝑣 𝑚𝑎𝑥 𝑡𝑓 −
𝑣 𝑚𝑎𝑥
2
𝑎 𝑚𝑎𝑥
, 𝑡𝑓 < 𝑡 < 𝑡𝑓 + 2
• 𝑡𝑓 e 𝑣 𝑚𝑎𝑥 sono stati calcolati in funzione di L, lunghezza della curva.

17. Verifica - 1
• Partendo dalla posizione di calibrazione l’errore è:

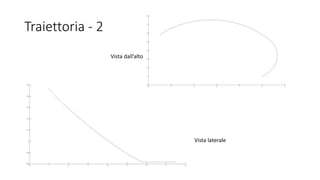
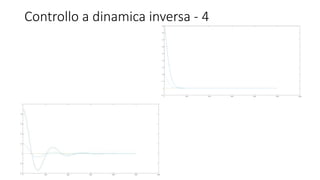
18. Verifica - 2
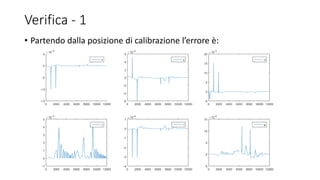
• Partendo dalla posizione 𝑞1 = [0.5; 0.5; 0; −
𝑝𝑖
2
; 0 ; 0.1; 1.2; 0.9]
l’errore è:

19. Controllo giunti
• L’obiettivo, data una traiettoria nello spazio giunti, è quello di far
inseguire la traiettoria ai giunti.
• Si usa il modello dinamico del manipolatore:
𝐵 𝑞 𝑞 + 𝐶 𝑞, 𝑞 𝑞 + 𝐹 𝑞 + 𝑔 𝑞 = 𝑢
• Sono stati ignorati contributi di attrito statico e forze esterne agenti
sul sistema.

20. Simulazioni
• Ai fini del test, sono state utilizzate due traiettorie.
• Traiettoria costante: si tenta di imporre, per 5 s ad un passo di
campionamento T=0.001 s, 𝑞 =
0.5 0.5 0 −
𝜋
2
0 0.1 1.2 0.9
𝑇
partendo dalla
configurazione di calibrazione 𝑞0 = 0 0 0 −
𝜋
2
0 0 0 0
𝑇
• Traiettoria generata nel secondo homework.

21. Controllo PD + gravità -1
• La strategia di controllo PD + gravità prevede di generare le coppie ai
giunti come composizione di tre contributi:
• Contributo proporzionale alla differenza tra posizione dei giunti desiderata e
posizione reale.
• Contributo proporzionale alla differenza tra velocità dei giunti desiderata e
velocità reale
• Contributo pari al contributo gravitazionale del modello dinamico.
𝑢 = 𝐾𝑝 𝑞 𝑑 − 𝑞 − 𝐾 𝑑 𝑞 + 𝑔(𝑞)
• La strategia converge senza errori per traiettorie costanti.

22. Controllo PD + gravità - 2

23. Controllo PD + gravità - 3
• La simulazione è stata effettuata variando i parametri 𝐾𝑝 e 𝐾 𝑑,
impostando entrambe le matrici come matrici diagonali con un valore
fisso sulla diagonale principale e variando questo valore tra 10, 100 e
200, scelti in maniera euristica.
• 𝐾𝑝 = 𝐾 𝑑 =
𝜆 0
0 𝜆
⋯
0 0
0 0
⋮ ⋱ ⋮
0 0
0 0
⋯
𝜆 0
0 𝜆

24. Controllo PD + gravità - Simulazioni

25. Controllo a dinamica inversa - 1
• La strategia a Dinamica Inversa prevede di compensare la dinamica
del manipolatore in toto.
𝑢 = 𝐵 𝑞 𝑦 + 𝐶 𝑞, 𝑞 𝑞 + 𝐹 𝑞 + 𝑔 𝑞
𝑦 = 𝑞 𝑑 + 𝐾 𝑑 𝑞 𝑑 − 𝑞 + 𝐾𝑝(𝑞 𝑑 − 𝑞)
• Questo permette di ottenere l’equazione dell’errore 𝑒 + 𝐾 𝑑 𝑒 + 𝐾𝑝 𝑒 =
0 avendo posto 𝑒 = 𝑞 𝑑 − 𝑞.
• Questo porta ad un errore che converge a zero, considerando che le
matrici delle costanti di retroazione sono definite positive.

26. Controllo a dinamica inversa - 2

27. Controllo a dinamica inversa - 3
• Costanti di retroazione 𝐾 𝑝 e 𝐾 𝑑 come matrici diagonali basate su i due
parametri che caratterizzano gli autovalori del sistema, 𝜁 e 𝜔 𝑛.
• 𝐾 𝑝 =
𝜔 𝑛
2
0
0 𝜔 𝑛
2 ⋯
0 0
0 0
⋮ ⋱ ⋮
0 0
0 0
⋯
𝜔 𝑛
2
0
0 𝜔 𝑛
2
𝐾 𝑑 =
2𝜁𝜔 𝑛 0
0 2𝜁𝜔 𝑛
⋯
0 0
0 0
⋮ ⋱ ⋮
0 0
0 0
⋯
2𝜁𝜔 𝑛 0
0 2𝜁𝜔 𝑛
• 𝜔 𝑛 è posto pari a 10 e 𝜁 prima pari a 1, per eliminare le oscillazioni, e poi
pari a 0.3, tenendo quindi in conto le oscillazioni nell’errore, per la
traiettoria costante.
• Per la traiettoria non costante si è posto 𝜁 pari a 1.

28. Controllo a dinamica inversa - 4

29. Controllo a dinamica inversa - 5