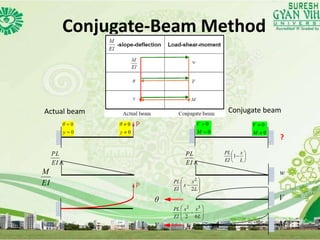
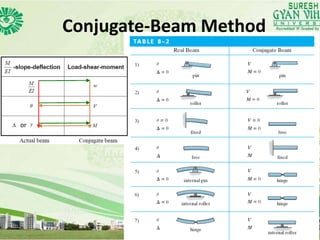
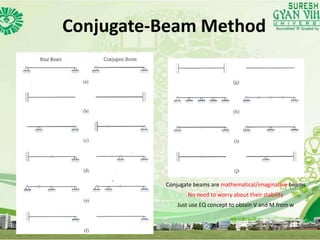
The document discusses the conjugate-beam method for analyzing indeterminate beams. It states that the conjugate-beam method uses a mathematical analogy between the slope-deflection equations of the actual beam and the load-shear-moment equations of an imaginary conjugate beam. It notes that the conjugate beam has the same deflected shape and internal forces as the actual beam, allowing the internal forces in the actual beam to be determined. The document provides equations showing the mathematical equivalence between the actual beam and conjugate beam and illustrates determining the internal forces at different points along the beams.

1. Subject Name: Theory of Structures
Topic Name:Analysis of Indeterminate
Beams
Lecture No: 8
Dr.Omprakash Netula
Professor & HOD
Department of Civil Engineering
7/24/2017 Lecture Number, Unit Number 1

2. Conjugate-Beam Method
• Mathematical analogy
-slope-deflection Load-shear-moment
EI
M
EI
M
dx
dθ

θ
dx
dy

EI
M
dx
yd
2
2
w
dx
dV

V
dx
dM

w
dx
Md
2
2

3. Conjugate-Beam Method
• Mathematical equivalence
-slope-deflection Load-shear-moment
EI
M
EI
M
θ
y
w
V
M
Actual beam Conjugate beam

4. Conjugate-Beam Method
P
EI
M
EI
PL
Actual beam Conjugate beam
0
0


y
θ
0
0


y
θ
0
0


M
V
0
0


M
V
EI
PL
w
V







L
x
EI
PL
1









L
x
x
EI
PL
2
2









L
xx
EI
PL
62
32
P
My
θ
?

5.  or
Conjugate-Beam Method

6. Conjugate-Beam Method
Conjugate beams are mathematical/imaginative beams
No need to worry about their stability
Just use EQ concept to obtain V and M from w