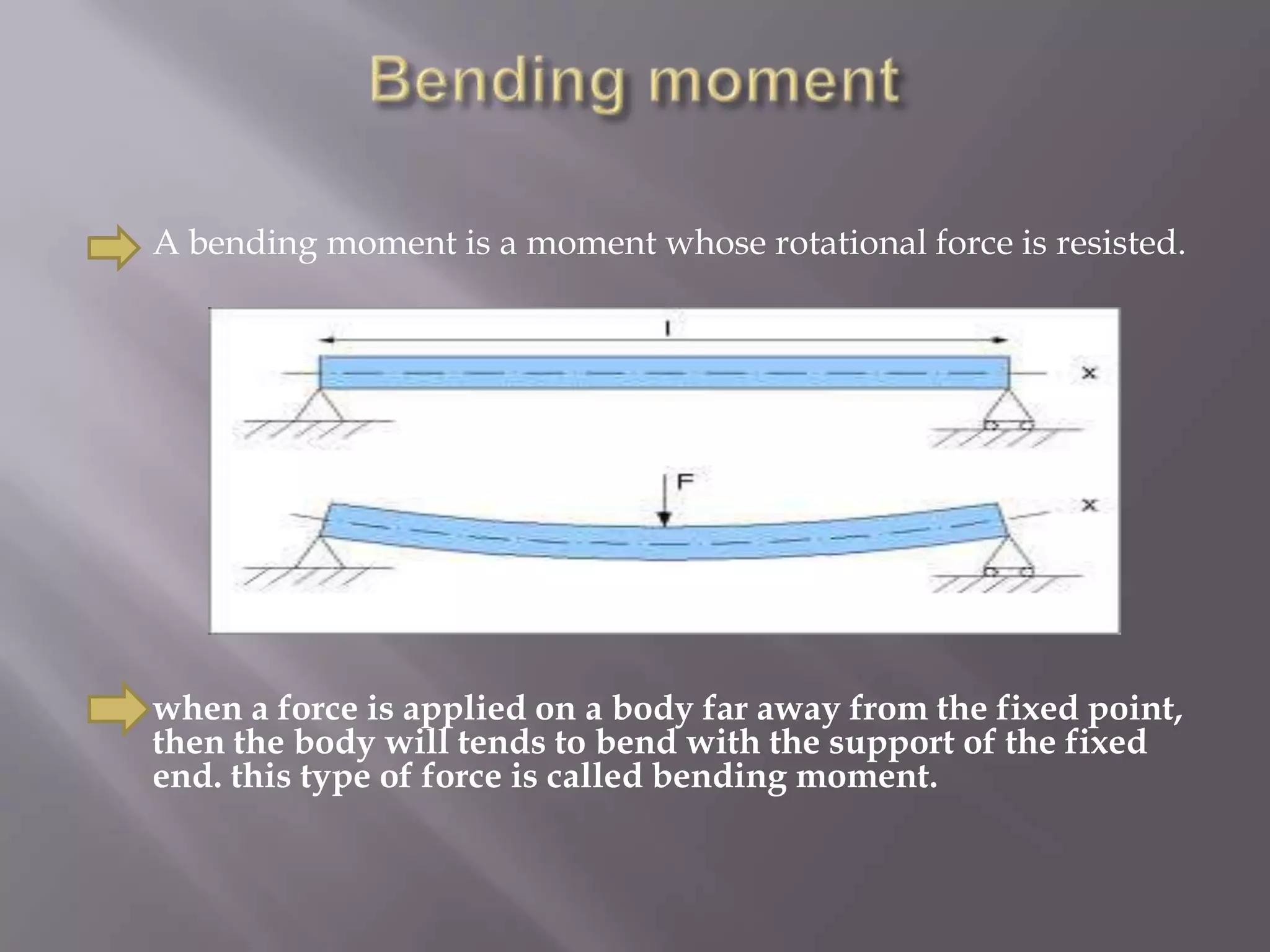
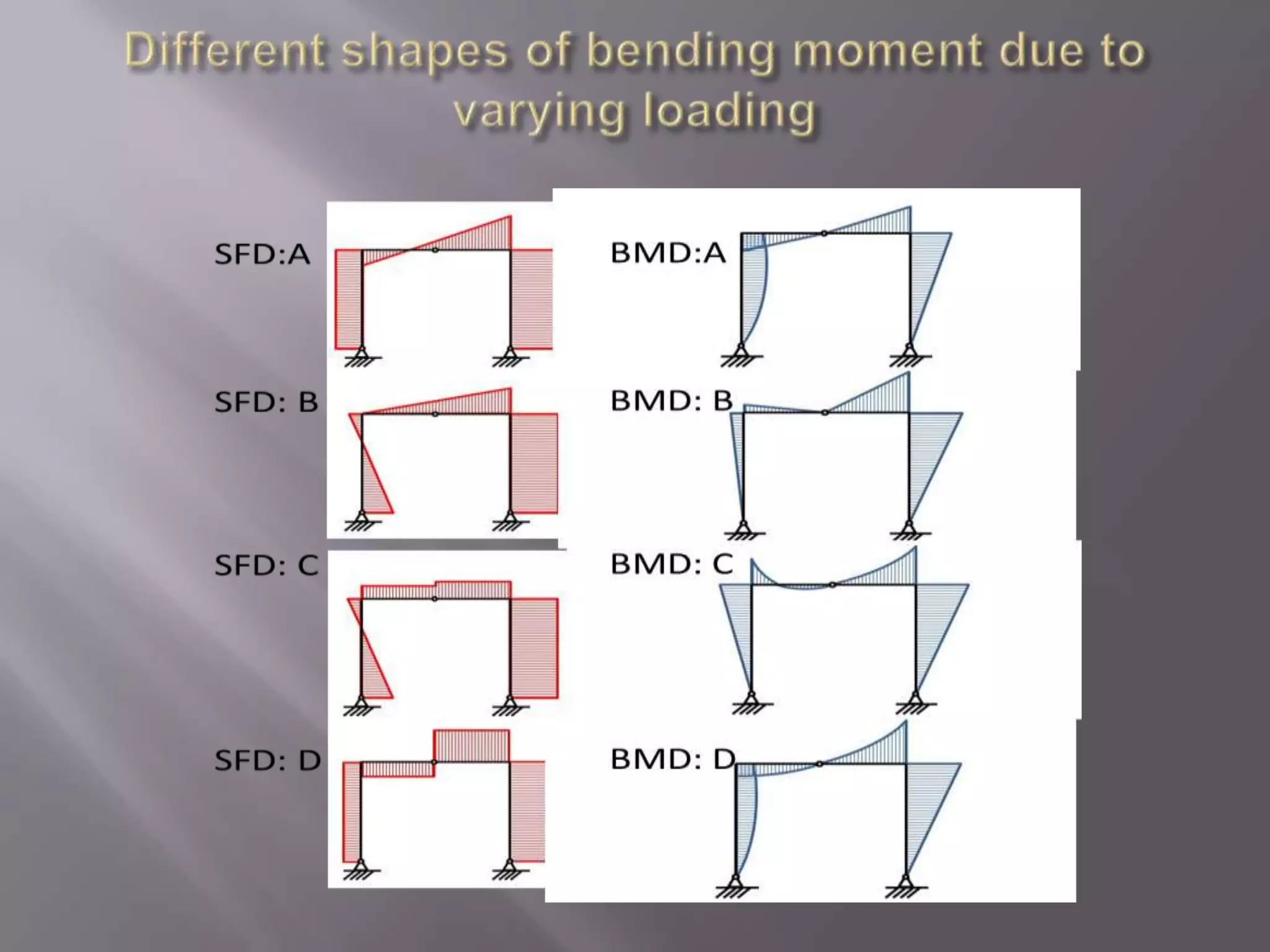
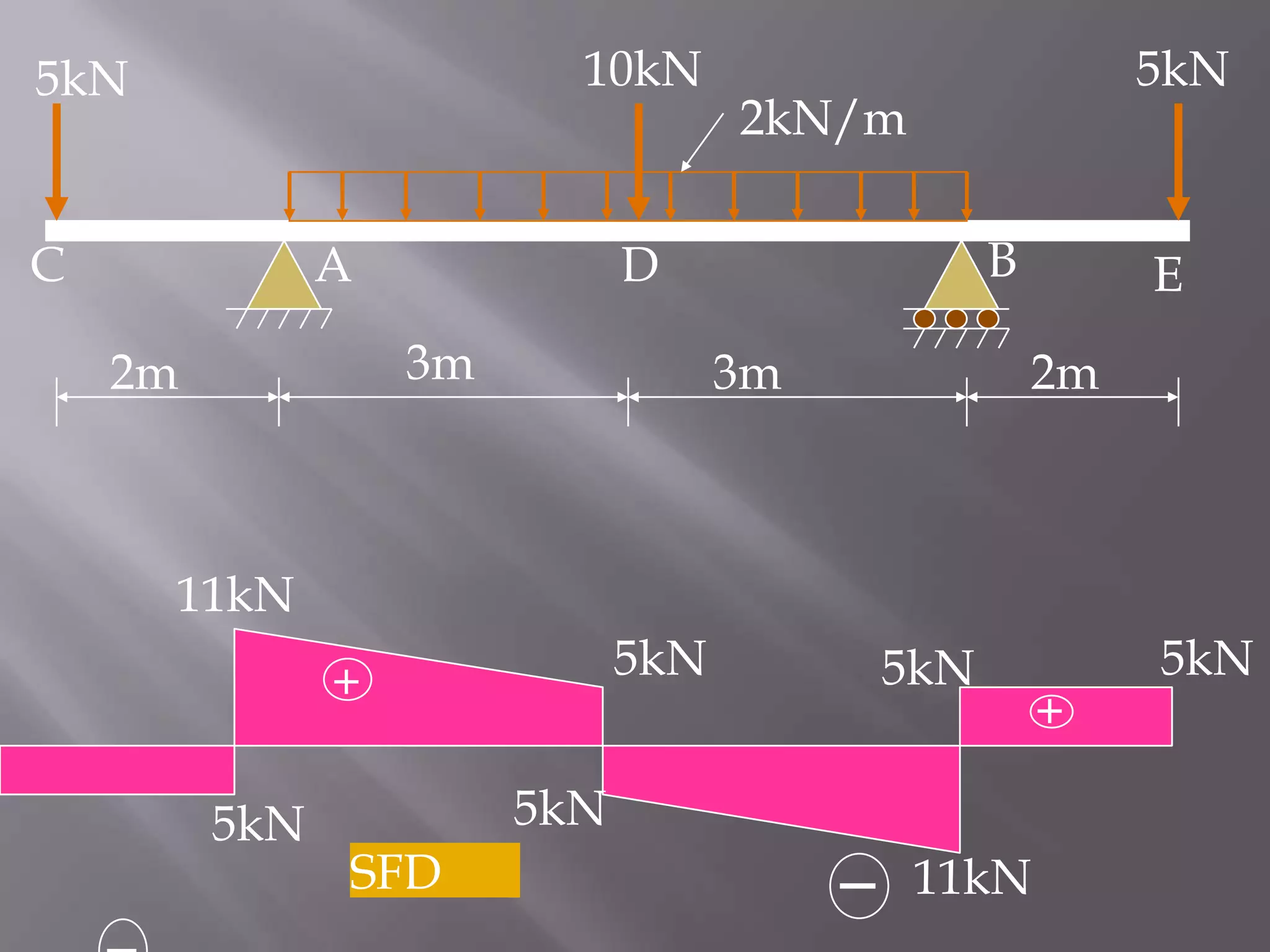
1) Bending moment is a measure of the bending effect on a beam due to applied forces and is measured in units of Newton-meters or foot-pounds force. 2) The bending moment equation is the algebraic sum of the moments about a section of the beam from all forces acting on one side. 3) Positive bending moments cause tension in the bottom fibers and compression in the top fibers (sagging) while negative moments cause the opposite (hogging).

1. AHSANULLAH UNIVERSITY OF
SCIENCE AND TECHNOLOGY.
DEPARTMENT OF CIVIL ENGINEERING
4THYEAR AND 2nd SEMESTER
Pre-stress concrete design sessional (CE 416)

2. THIS IS IMRAN ISLAM.
ROLL: 10.01.03.066
Section : B

3. 

A bending moment is a moment whose rotational force is resisted.
when a force is applied on a body far away from the fixed point,
then the body will tends to bend with the support of the fixed
end. this type of force is called bending moment.

5. 

Bending moment is an important factor to be
consider while designing any structural
component. For example we consider the
following which shows the free body diagram
Of a simply supported beam

6. Based on these sign conventions we can write the
equation of bending moment at section X-X as given
below;
Considering forces on the left of the section X-X
MX = RALA - F 1X1 – F2 X2
Considering forces to the right section of X-X.
MX = RB LB - F 3X3 – F4 X4.

7. The above expression is called as banding moment equation
which can be written depending upon the loading on the
beam. A graphical representation of the bending moment
equation along the span of the beam is known as bending
moment diagram(BMD).
‘’It is also defined as the algebraic sum of the moments
about a section of the beam concerned of all the forces acting
on one side of the section’’.

8. 
A bending moment is a measure of the bending
effect due to forces acting on a beam. It is a
type of stress and is measured in terms of force
and distance. so they have as unit Newtonmetres (Ne-cm) , or foot-pounds force (ft-lb).

9. 
Sagging bending moment is taken as +ve. It results
in developing tension in the bottom fibres and
compression in top fibres of the beam. .

10. . Hogging bending moment is taken as –ve. And it
develops compression in the bottom fibres and tension
in the top fibres.

11. 
Positive and Negative are just directions. The
main concern is whether there exist a bending
moment or not. Sagging and hogging moments
are important to differentiate. This is of great
importance in designing reinforced concrete
members as we have to provide steel rebar in
the zone of beam having tensile stress as
concrete is weak in tension.

12. 10kN
5kN
5kN
2kN/m
C
A
2m
B
D
3m
3m
E
2m

13. 



Solution:
Calculation of Reactions:
Due to symmetry of the beam, loading and
boundary conditions, reactions at both
supports are equal.
.`. RA = RB = ½(5+10+5+2 × 6) = 16 kN

14. 10kN
1
2
3
4
5
1
2
3
4
5
2m






2kN/m
3m
RA=16kN
3m
6
7
8 9
6
7
8 9
2m
RB = 16kN
Shear Force Calculation: V0-0 = 0
V1-1 = - 5kN
V6-6 = - 5 – 6 = - 11kN
V2-2 = - 5kN
V7-7 = - 11 + 16 = 5kN
V3-3 = - 5 + 16 = 11 kN
V8-8 = 5 kN
V4-4 = 11 – 2 × 3 = +5 kN
V9-9 = 5 – 5 = 0(check)
V5-5 = 5 – 10 = - 5kN

15. 10kN
5kN
C
A
2kN/m
B
D
3m
2m
5kN
3m
E
2m
11kN
5kN
+
5kN
5kN
5kN
SFD
11kN
+
5kN

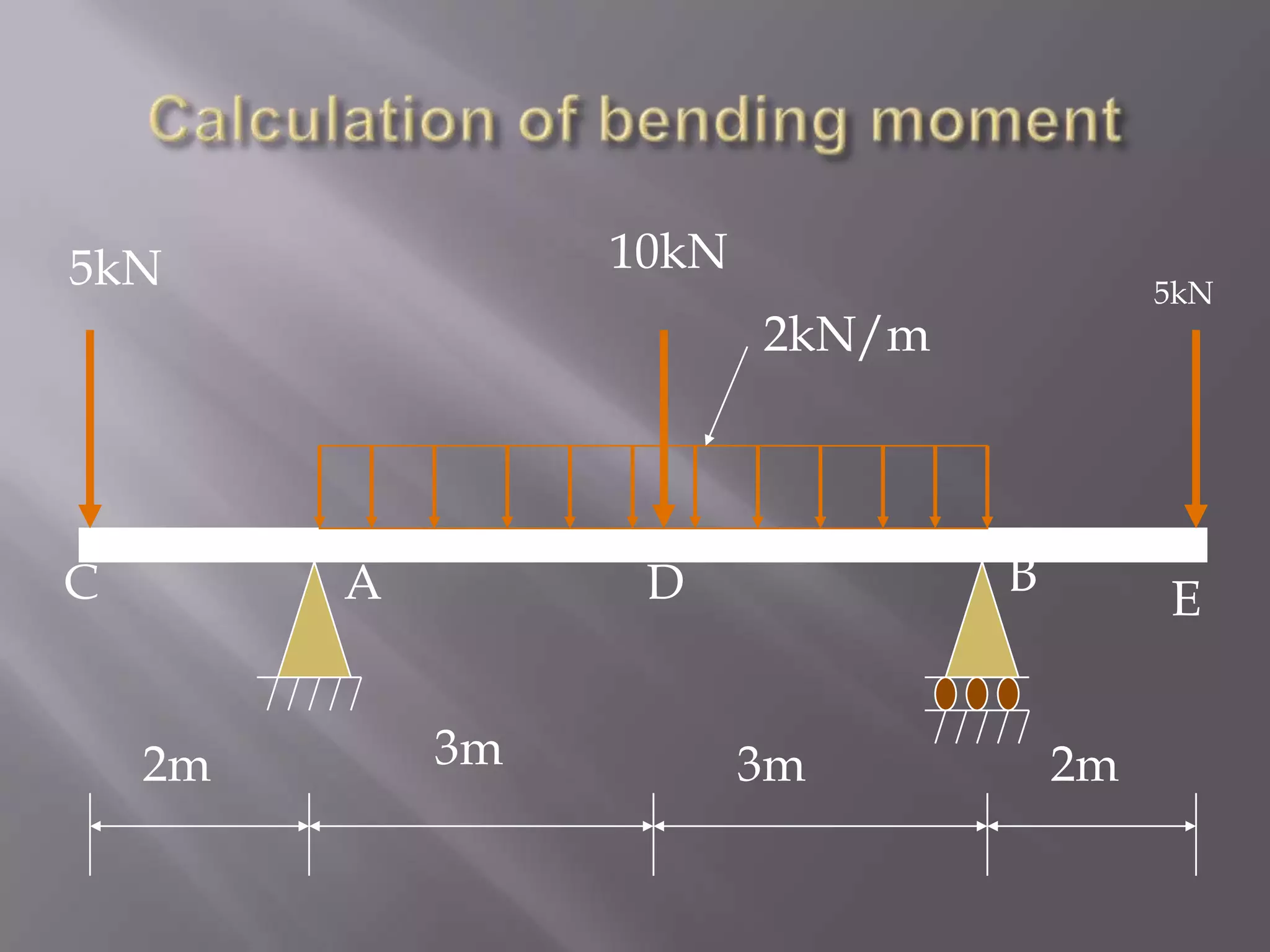
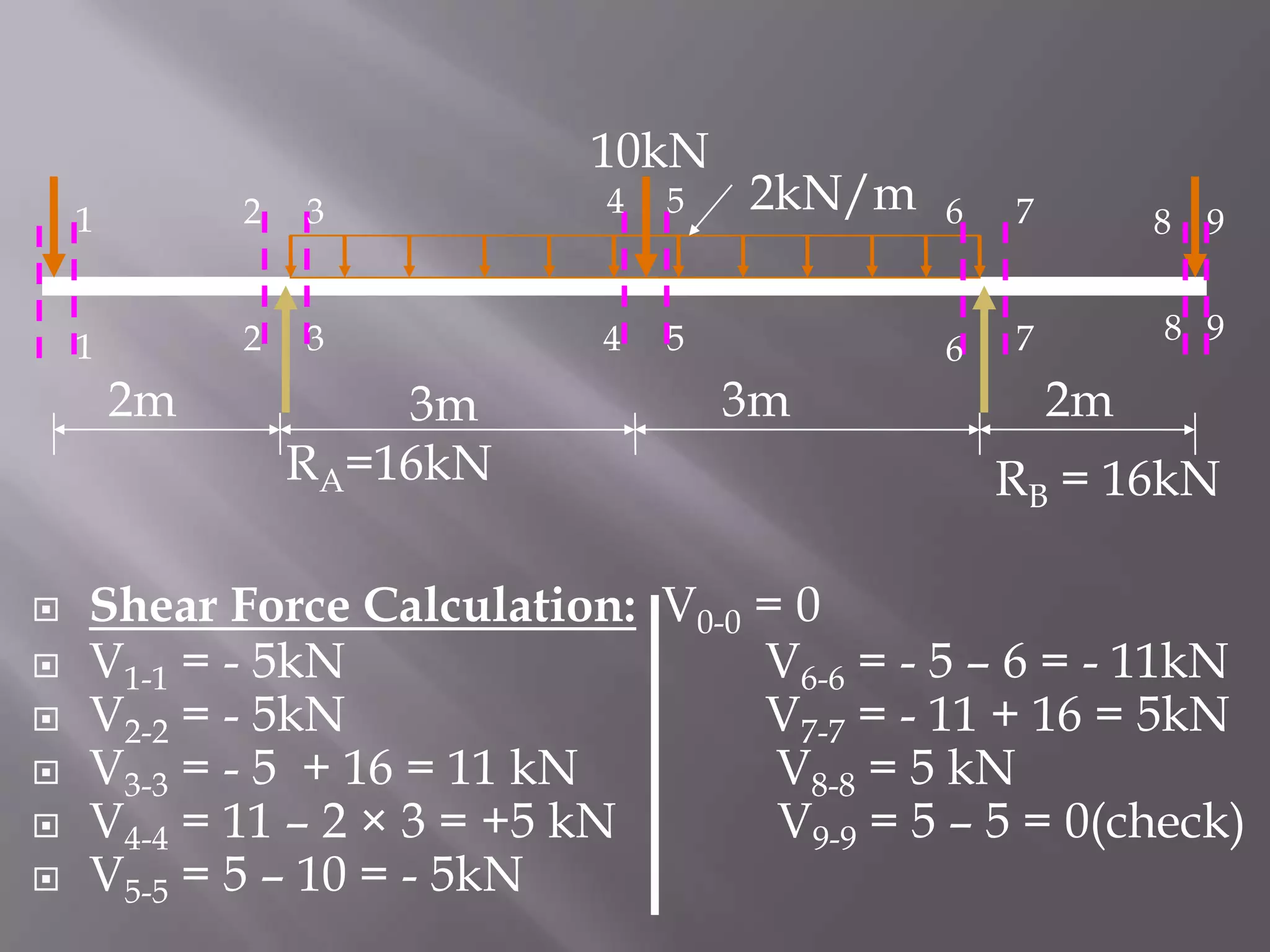
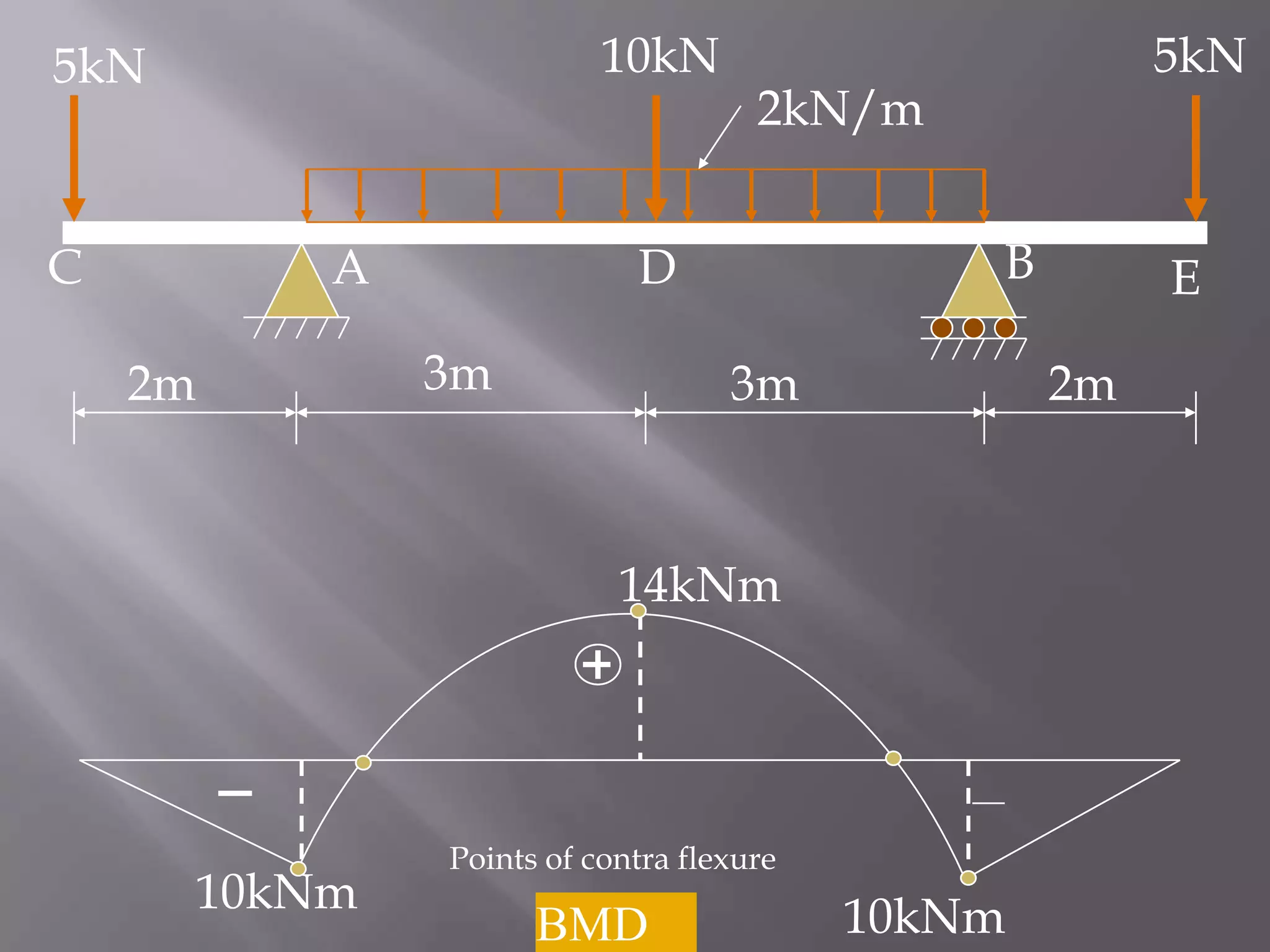
16. 10kN
5kN
C
A
RA=16k
2kN/m
B
D
3m
2m
5kN
3m
E
2m
RB = 16kN
Bending Moment Calculation:
MC = ME = 0 [Because Bending moment at free end is
zero]
MA = MB = - 5 × 2 = - 10 kNm
MD = - 5 × 5 + 16 × 3 – 2 × 3 × 1.5 = +14 kNm

17. 10kN
5kN
C
A
2kN/m
B
D
3m
2m
5kN
3m
2m
14kNm
10kNm
Points of contra flexure
BMD
E
10kNm

18. 

It is the point on the bending moment diagram
where bending moment changes the sign from
positive to negative or vice versa.
It is also known as ‘inflection point’. At the
point of inflection point or contra flexure the
bending moment is zero.

19. 
This depends on the arrangement of a beam or column.
for a simply supported beam with a point load in the
centre of the beam
Mmax = WL/4 and will occur at centre span
W is the load in kN
L is the span in m
Moment is given in kNm
for a uniformly distributed load w given in kN/m
Mmax = wL^2/8 and will occur at centre span.

21. 


the points where bending moments are maximum are
points of maximum stress , therefore these points
require more reinforcement with steel to counter the
stresses , Where as at points where stresses are less
, curtailment of steel can be done .
To avoid the bending of member reinforcement is
used.
bending moment is required for design of any
structural component and also for the calculation of
slope and deflection of structure