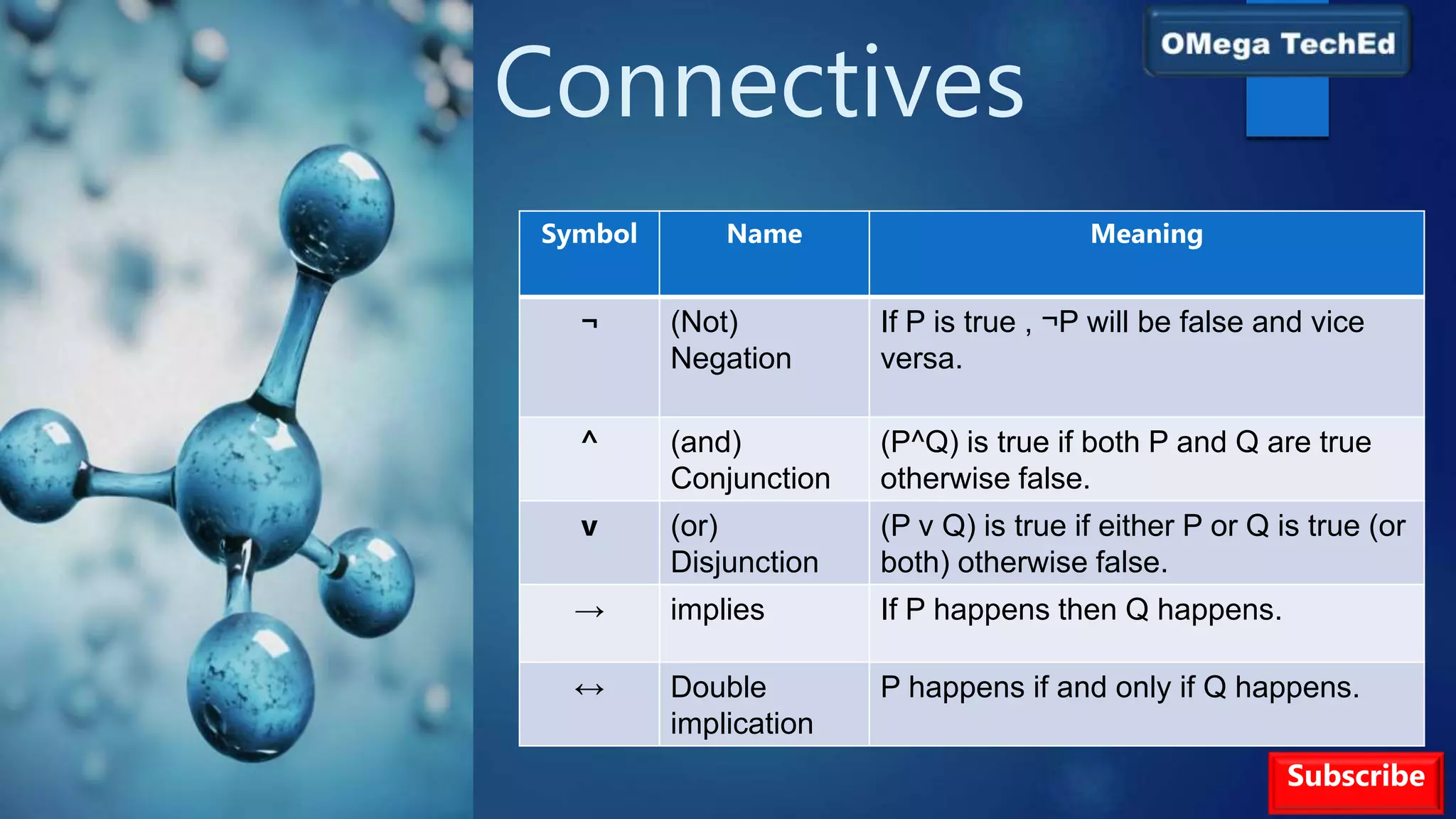
Knowledge-based agents can accept new tasks in the form of explicitly described goals and adapt to changes in their environment by updating relevant knowledge. They maintain a knowledge base of facts about the environment and use an inference engine to deduce new information and determine what actions to take. The knowledge base stores sentences expressed in a knowledge representation language and the inference engine applies logical rules to deduce new facts or answer queries. Propositional logic is often used to represent knowledge, where sentences consist of proposition symbols connected by logical connectives like AND, OR, and NOT.

1. Knowledge-based agent
18
Propositional Logic

2. Subscribe
Knowledge-Based (Logical) Agents
Knowledge-based agents can accept new
tasks in the form of explicitly described
goals; they can achieve competence quickly
by being told or learning new knowledge
about the environment; and they can adapt
to changes in the environment by updating
the relevant knowledge.

3. Components
Knowledge Base
• A knowledge base is a set of sentence. Each sentence is
expressed in a language called a knowledge representation
language and represents some assertion about the world.
Inference Engine
• Inference engine allows us to add a new sentence to the knowledge base. A sentence is a
proposition about the world. Inference system applies logical rules to the KB to deduce new
information.
Subscribe

4. Operations performed by K.B.A.
 A Knowledge Base keeps track of things.
 We can TELL it facts or ASK for inference.
TELL: This operation tells the knowledge base what it perceives from the
environment.
ASK: This operation asks the knowledge base what action it should
perform.
Example:
TELL: Father of John is Robbin.
TELL: Marry is John’s sister.
TELL: John’s father is the same as John’s sister’s father.
ASK: Who is Marry’s father?
Subscribe

5. Each time when the function is called, it does three things.
It TELLs the KB what it perceives.
It ASKs KB what action it should take
Agent program TELLS the KB that which action was chosen.
Subscribe

6. Logic
 Knowledge bases consist of sentences.
 These sentences are expressed according to the
syntax of the representation language , which
specifies all the sentences that are well formed.
 x+y=2 (well formed)
 x2y=+ (not well formed)
 A logic must also defines the semantics or
meaning of sentences.
 The semantics defines the TRUTH of each
sentence with respect to each possible
world.(model)
 x+ y=4 is true in a world where x=2 and y=2
But false in a world where x is 1 and y is 1
Subscribe

7. Propositional Logic
Subscribe
 The Syntax of propositional logic defines the allowable
sentences.
The atomic sentences consist of a single proposition
symbol Each such symbol stands for a proposition that
can be true or false.
Example: Sunday is Holiday. (true proposition)
2+1=4 (False proposition)
some boys like to play cricket.(Not a propositional logic)
 Complex sentences are constructed from simpler
sentences, using parentheses and logical connective.

8. Connectives
Symbol Name Meaning
¬ (Not)
Negation
If P is true , ¬P will be false and vice
versa.
^ (and)
Conjunction
(P^Q) is true if both P and Q are true
otherwise false.
v (or)
Disjunction
(P v Q) is true if either P or Q is true (or
both) otherwise false.
→ implies If P happens then Q happens.
↔ Double
implication
P happens if and only if Q happens.
Subscribe

9. Examples:
1.You can use the college library only if you are a
student or are a faculty.
P(Q v R)
2. I will go for shopping if and only if I have a money.
P↔Q
3. "If it rains, I will not go to the market.
P⌐Q
4. It is not cloudy, and it is not raining.
⌐P ^ ⌐Q
Some dog is a pet.
Everybody loves someone.
Subscribe

10. Thanks For
Watching
Reference:
Artificial Intelligence
A Modern Approach Third Edition
Peter Norvig and Stuart J. Russell
Subscribe
Like
Share
Next Topic: The Wumpus World

11. OMega TechEd
About the Channel
This channel helps you to prepare for BSc IT and BSc computer science subjects.
In this channel we will learn Business Intelligence ,Artificial Intelligence, Digital Electronics,
Internet OF Things Python programming , Data-Structure etc.
Which is useful for upcoming university exams.
Gmail: omega.teched@gmail.com
Social Media Handles:
omega.teched
megha_with
Subscribe