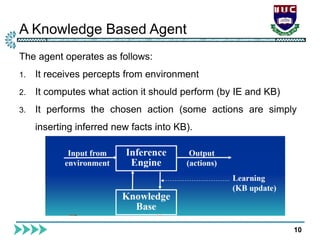
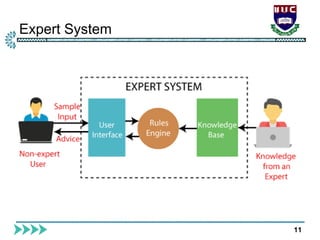
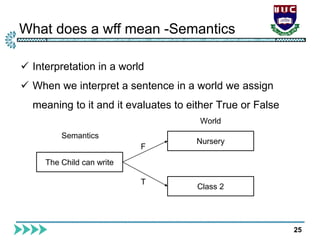
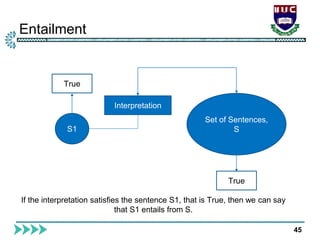
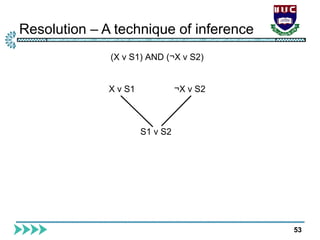
The document is a lecture from International Islamic University Chittagong on logical reasoning and propositional logic in artificial intelligence. It covers topics such as knowledge representation, reasoning methods, kinds of logical agents, and detailed structure on propositional and first-order logic. Additionally, it discusses inference rules, satisfiability, resolution, and the applications of these concepts in AI systems.

1. 1
International Islamic University Chittagong
January 22, 2024
Tashin Hossain
Department of Computer Science and Engineering
Lecture#7
Agents that Reason Logically
And Propositional Logic
Adjunct Lecturer

2. Course Information
2
Course Materials:
1. Stuart Russell, Peter Norvig: “Artificial Intelligence A
Modern Approach”, 3rd Edition.
2. Other specific materials and lecture slides

3. Course Information
3
Segment Contents
03
Game playing: Introduction, Perfect Decisions, Imperfect
Decisions, Alpha-Beta Pruning.
Constraints satisfaction problem: Travelling salesman problem,
graph coloring etc.
04
Propositional and First-Order logic: Knowledge
Representation, Reasoning and Logic; Propositional Logic:
Syntax, Semantics, Validity and Inference, Rules of Inference for
Propositional logic; First-Order Logic: Syntax and Semantics,
Using first-order logic.
Inference in first order logic: Inference Rules Involving
Quantifiers, Example Proof, Generalized Modus Ponens, Forward
and Backward Chaining, Completeness, Resolution.

4. Course Information
4
Segment Contents
05
Probabilistic Reasoning: Probability and Bayes’ Theorem,
Certainty Factors and Rule-Based Systems, Bayesian Networks,
Fuzzy Logic; Ds theory, ER
Some Expert Systems: Representation and Using Domain
Knowledge, Expert System Shells, Explanation, And Knowledge
Acquisition.
06
Learning: Introduction to Learning, Inductive Learning, Learning
Decision Trees, Neural Net Learning;
07
Natural language processing: Introduction, Syntactic
Processing, Semantic Analysis, Discourse and Pragmatic
Processing.

5. 5
Agents that Reason
Logically

6. Knowledge and Reasoning
6
 From the previous lectures it has been shown that an agent that
has goals and searches for solutions to the goals can do better
than one that just reacts to its environment (simple reflex agent)
 We focused mainly on the question of how to carry out the search
(using different search strategies), leaving aside the question of
general methods for describing states and actions

7. Knowledge and Reasoning
7
 It is necessary to powering the agents with the capacity for general
logical reasoning
 A logical, knowledge-based agent begins with some knowledge of the
world and of its own actions
 It uses logical reasoning to maintain a description of the world as new
precepts arrive and to deduce a course of action that will achieve its goals
 In this lecture we introduce the basic design for a knowledge-
based agent, followed by a simple logical language for expressing
knowledge, and show how it can be used to draw conclusions
about the world and to decide what to do

8. A Knowledge Based Agent
8
 A knowledge-based agent consists of a knowledge base
(KB) and an inference engine (IE)
 A knowledge-base is a set of representations of what one
knows about the world (objects and classes of objects, the
fact about objects, relationships among objects, etc.)
 Each individual representation is called a sentence
 The sentences are expressed in a knowledge representation
language

9. A Knowledge Based Agent
9
 Examples of sentences
– The moon is made of green cheese  Fact
– If A is true then B is true  Rule
– A is false
– All humans are mortal
– Confucius is a human
 The Inference engine derives new sentences from the input
and KB
 The inference mechanism depends on representation in KB

10. A Knowledge Based Agent
10
The agent operates as follows:
1. It receives percepts from environment
2. It computes what action it should perform (by IE and KB)
3. It performs the chosen action (some actions are simply
inserting inferred new facts into KB).

11. Expert System
11

12. KB can be Viewed at Different Levels
12
 Knowledge Level
– The most abstract level
– describe agent by saying what it knows
– Example: A taxi agent might know that the Golden Gate Bridge
connects San Francisco with the Marin County
 Logical Level
– The level at which the knowledge is encoded into sentences
– Example: Links(GoldenGateBridge, SanFrancisco, Marin-County)
 Implementation Level
– The physical representation of the sentences in the logical level
– Example: “Links (GoldenGateBridge, SanFrancisco, MarinCounty)”

13. 13
Propositional Logic

14. What is Proposition?
14
 A proposition is a statement that can be either true or
false; it must be one or the other, and it cannot be both
 The sun rises in the east
 Today is a very hot day

15. Knowledge and Intelligence
15
 Does knowledge has any role in demonstrating
intelligent behavior?

16. Logic is a Formal Language
16
 Propositional Logic
 Rahima is intelligent - proposition
 Rahima is hardworking – proposition
 If Rahima is intelligent and Rahima is hardworking
Then Rahima scores high marks -proposition

17. Elements of PL
17
 Rahima is intelligent => intelligent ( Rahima)
 Rahima is hardworking
Objects and Relations or functions
Elements

18. Towards the Syntax
18
 Intelligent (Rahima) == Rahima is intelligent
 Hardworking (Rahima) == Rahima is hardworking

19. Towards more syntax
19
o Let P stand for intelligent (Rahima) 
o Let Q stand for Hardworking (Rahima)  F
o What does P ˄ Q (P and Q) mean ? 
o What does P ˅ Q (P and Q) mean ? 
o P ˄ Q, P ˅ Q are compound propositions

20. Syntactic Elements of PL
20
o A set of propositional symbols (P, Q, R etc.)
o each of which can be True or False
o Set of logical operators :˄, ˅, Not, implies
o often parenthesis() is used for grouping
o There are two special symbols
o TRUE (T) and FALSE (F) – these are logical constants

21. How to form propositional sentence?
21
– Each symbol (a proposition or a constant) is a sentence
– If P is a sentence and Q is a sentence, Then
– (p) is a sentence
– P ˄ Q is a sentence
– P or Q is a sentence
– not P is a sentence
– P implies Q is a sentence
– Nothing else is a sentence
– Sentences are called world form formulae (wff)

22. Examples of WFFs
22
P , Q  True
– P and Q  True
– (P or Q) implies R  If the roads get wet, then it rains
– (P and Q) or R implies S
– Not (P or Q)
– Not (P or Q) implies R and S

23. Implication
23
 P implies Q P  Q
 If P is true then Q is true
 If it rains then the roads are wet
 Sufficient condition
 If the roads are wet then it rains ???

24. Equivalence
24
 P bidirectional Q
 Triangle
If two sides (A,B) of an triangle are equal (P), then
Opposite angles are equal (Q)
If opposite angles of a triangle are equal (Q), then two
sides of an triangle are equal (P)

25. What does a wff mean -Semantics
25
 Interpretation in a world
 When we interpret a sentence in a world we assign
meaning to it and it evaluates to either True or False
The Child can write
Nursery
Class 2
F
T
World
Semantics

26. Semantic of compound sentence
26
P: Likes ( Rahima, Sanjida)
Q: Knows (Tania, Farzana)
World: Rahima and Sanjida are friends and
Tania and Farzana known to each other
P= T, Q=T
P and Q =T
P and Not Q = F

27. Validity of a sentence
27
If a propositional sentence is true under all possible
interpretation, it is VALID
• Tautology
• Satisfiability
• Inconsistent
P v ¬ P = T
Question:

28. Validity of a sentence
28
• Tautology  Compound Proposition is always True
• Satisfiability  A compound sentence is satisfiable if there is at least
one true result in its Truth table
• Valid: A compound proposition is valid when it is a tautology
• Invalid: A compound proposition is invalid when it is either a
contradiction or contingency

29. Validity of a sentence
29
Inconsistency in propositional logic refers to a situation
where a set of propositions or statements leads to a
contradiction, meaning that it's impossible for all the
statements in the set to be simultaneously true
Let's consider a simple example:
Statement A: It is raining.
Statement B: It is not raining.

30. Quiz
30
Express the following English sentence in the
language of PL
– It rains in July  rains ( July)
– The book is not costly  not costly (book)
– If it rains today and one does not carry umbrella, then
he will be drenched
Rains(today) ^ not carry( umbrella)  drenched(he)

31. Quiz
31
If P is true and Q is true then are the followings true or
false
– P → Q
– (¬P∨Q) → Q
– (¬P^Q) → P
– P ∨ ¬P

32. 32
Inference in PL

33. Objectives
33
• Infer the truth value of a proposition
• Reason towards new facts, given a set of propositions
• Prove a proposition given a set of propositional facts

34. Procedure to derive Truth Value
34
P Q P^Q PvQ
F F F F
F T F T
T F F T
T T T T
P v Q will be True when any of them is True
P ^ Q will be True when both of them are True

35. Procedure to derive Truth Value
35
P Q P  Q
F F T
F T T
T F F
T T T
If you won’t reach the station on time, then you won’t be able to catch
the train  T
If P is True, then Q is True, since P is a sufficient condition so that Q is
True

36. De Morgan’s Law
36
1. ¬ ( P ^ Q ) = ¬P v ¬ Q
2. ¬ ( P v Q ) = ¬P ^ ¬ Q
Prove the De morgan’s law using Truth
table

37. Reasoning
37
• P: It is the month of July
• Q: It rains
• R: P→Q
• If it is the month of July then it rains
• It is the month of July
• Conclude: It rains

38. Reasoning
38
P→Q
P
----------
Q ( it rains)
This type of reasoning is called deductive reasoning

39. Reasoning –Modus Ponens
39
• Modus Ponens is very much a valid inference
rule prove
P  Q ¬P v Q
Prove:
 (¬P v Q) ^ P
 (¬P v P) v Q
 T v Q
 Q

40. Valid inference rule
40
• Thus Irrespective of meaning modus ponens allow us to
infer the truth of Q
• Modus Ponens is a inference rule that allow us to
deduce the truth of a consequent depending on the truth
of an antecedents

41. Satisfiability
41

42. Satisfiability
42

43. Entailment
43

44. Entailment
44

45. Entailment
45
Set of Sentences,
S
S1
Interpretation
True
True
If the interpretation satisfies the sentence S1, that is True, then we can say
that S1 entails from S.

46. Entailment
46

47. 47

48. Clauses: A Special Form
48

49. Converting a compound proposition to
the clausal form
49

50. Converting a compound proposition to
the clausal form
50

51. Converting a compound proposition to
the clausal form
51
Example: Consider the Sentence
¬ ( A  B) v (C  A)
1. Eliminate the Implication Sign
¬ (¬A v B) v (¬ C v A)
2. Eliminate the double negation and reduce scope of “not”
signs
(A ^ ¬ B) v (¬C v A)
3. Convert to conjunctive normal form by using distributive and
associative law
(A ^ ¬ B) v (¬C v A) => Distributive Law: A(B+C) = AB + AC
 ( A v ¬C v A) ^ (¬B v ¬C v A)
 ( A v ¬C) ^ (¬B v ¬C v A)
4. Get the set of clauses
 ( A v ¬C)
 (¬B v ¬C v A)

52. Resolution – A technique of inference
52

53. Resolution – A technique of inference
53
(X v S1) AND (¬X v S2)
X v S1 ¬X v S2
S1 v S2

54. An Example
54

55. Convert the Sentences into PL
55

56. Convert the Sentences into Clausal Form
56

57. Proof by Refutation
57

58. Procedure of Resolution
58

59. Quiz
59

60. 60
First Order Logic

61. Objectives
61

62. Objectives
62

63. Limitations of PL
63

64. Limitations of PL
64

65. Limitations of PL
65

66. The Problem of Infinite Model
66

67. FOL/Predicate Logic
67

68. What added in FOL?
68

69. Terms
69

70. Terms: Constants and Variables
70

71. Terms: Functions
71

72. Functions: Example
72

73. Functions with Variable Arguments
73

74. Predicates
74

75. Types of Predicates
75

76. Formulation of Predicates
76

77. Predicate Examples
77

78. Quantifiers
78

79. Universal Quantifiers
79

80. Universal Quantifiers
80

81. Quiz Problem Revisited
81

82. Existential Quantifier
82

83. Duality of Quantifiers
83

84. Sentences
84

85. Exercise
85

86. 86
Reasoning in FOL

87. Example of Sentences
87

88. Example of Sentences
88

89. Example of Sentences
89

90. Alternative Representation
90

91. FOL with Equality
91

92. Exercise Revisited
92

93. Exercise Revisited
93

94. Inference Rules
94

95. Inference Rules
95

96. Reasoning in FOL
96

97. Representation in FOL
97

98. Inferencing
98

99. Inferencing (contd.)
99

100. Horn Sentences
100

101. Horn Sentences
101

102. Horn Sentences
102
Continue…

103. Next Lecture
103