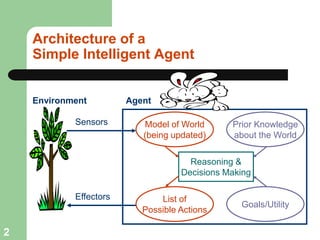
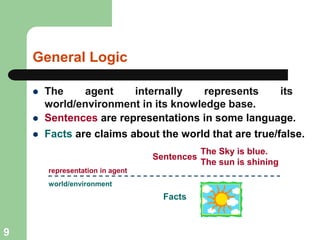
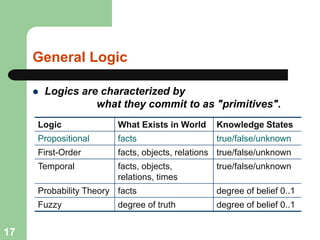
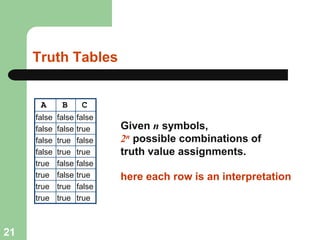
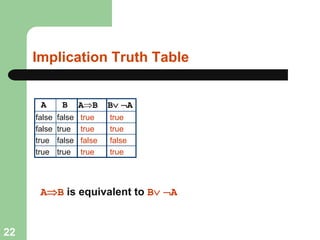
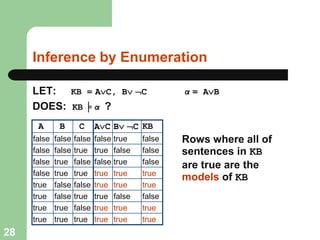
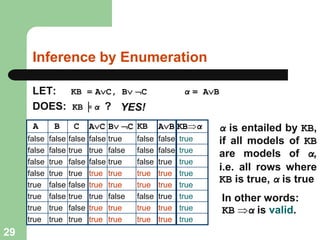
This document discusses logical agents and knowledge representation in artificial intelligence. It describes the architecture of a simple logical agent that uses sensors to perceive the environment, effectors to take actions, and a knowledge base to represent its knowledge and make reasoning and decisions. The knowledge base contains facts about the world represented as sentences in a formal logic. The agent can ask the knowledge base questions and incorporate new percepts to update its internal representation of the world. Logical inference allows the agent to deduce new facts that follow logically from the knowledge base without needing to understand the meaning of the sentences. Different types of logic like propositional, first-order, and temporal logic are discussed for knowledge representation.

1. CSE 412:
Artificial Intelligence
Topic – 5: Logical Agents
Contents:



Spring 2017

2. Architecture of a
Simple Intelligent Agent
Environment Agent
Sensors
Effectors
Reasoning &
Decisions Making
Model of World
(being updated)
List of
Possible Actions
Prior Knowledge
about the World
Goals/Utility
2

3. Knowledge Based Agent
 Knowledge base:
– A knowledge base (abbreviated KB or kb) is a special
kind of database for knowledge management.
– A knowledge base is an information repository that
provides a means for information to be collected,
organized, shared, searched and utilized.
– The part of an expert system that contains the facts
and rules needed to solve problems.
– A collection of facts and rules for problem solving.
3

4. Knowledge Based Agent
 The agent must be able to:
– represent states, actions, etc.
– incorporate new percepts
– update internal representation of world
– deduce hidden properties of world
– deduce appropriate actions
 One of the core problems in developing an
intelligent agent is knowledge representation:
– how to represent knowledge
– how to reason using that knowledge
4

5. Knowledge Bases (KB)
 A knowledge base:
– contains the domain-specific content for an agent
– is a set of representations of facts about the world
 is a set of sentences in a formal language
 Building the KB:
– learning: agent discovers what it knows
– telling: agent is given what it knows (declarative)
5

6. Knowledge Bases (KB)
 Main actions of intelligent agent:
– TELL information to KB in the form of percept
– ASK KB what to do in the form of action
 Answers should follow from KB.
Agent should not make things up!
 An inference engine is composed of domain-
independent algorithms that are used to
determine what follows from the knowledge
base.
6

7. Knowledge Bases (KB)
 View of agent (levels of abstraction):
– knowledge level:
what the agent knows at a high level
– logic level:
level of sentence encoding
– implementation level:
level that runs on the architecture,
detail of data structures and algorithms.
7

8. Algorithm
8

9. General Logic
 The agent internally represents its
world/environment in its knowledge base.
The Sky is blue.
The sun is shining
representation in agent
world/environment
 Sentences are representations in some language.
 Facts are claims about the world that are true/false.
Sentences
Facts
9

10. General Logic
 Sentences represent facts in the world.
Sentences
Facts
representation in agent
world/environment
 Meaning connects sentences to their facts.
Meaning / Interpretation
 A sentence is true if what it represents is
actually the case in the current state of world.
Time flies.
10

11. General Logic
repr.
world
Knowledge Conclusions
infer
follows
Facts New Facts
 Proper reasoning ensures that conclusions
inferred from the KB are consistent with reality.
That means they represent new facts that actually
follow from the original facts (represented by sentences
in the KB).
11

12. Conclusions
General Logic
repr.
world
Knowledge
infer
 Computers don't know the meaning.
 A mechanical inference procedure is needed that
derives conclusions without needing to know the
meaning of the sentences.
Sentences New Sentences
entails
follows
Facts New Facts
12

13. Entailment
 KB ╞ α
Knowledge base KB entails sentence α
if and only if α is true in all worlds where KB is true
13

14. Entailment
 KB ╞ α
Knowledge base KB entails sentence α
if and only if α is true in all worlds where KB is true
 For example:
KB: "sky is blue" = true, "sun is shining" = true
entails α: "sky is blue and sun is shining" = true
– α represents a true fact
as long as facts represented in KB are true
– if the sky was actually cloudy then KB isn't the true world state
then α wouldn't represent a true fact
 Entailment requires sentences in KB to be true.
14

15. Logical Inference
 Inference procedure can:
– generate new sentences α entailed by KB
– determine whether or not a given sentence α
is entailed by KB (i.e. prove α)
15

16. General Logic
 Logics are formal languages for representing
information from which conclusions can be drawn.
16

17. General Logic
 Logics are characterized by
what they commit to as "primitives".
Logic What Exists in World Knowledge States
Propositional facts true/false/unknown
First-Order facts, objects, relations true/false/unknown
Temporal facts, objects,
relations, times
true/false/unknown
Probability Theory facts degree of belief 0..1
Fuzzy degree of truth degree of belief 0..1
17

18. Propositional Logic (PL) Basics
 propositions: assertions about an aspect of a world
that can be assigned either a true or false value
– e.g. SkyIsCloudy, JimIsHappy
– True, False are propositions meaning true and false
18

19. Logical Connectives of PL
 S negation (not)
 S1S2 conjunction (and)
S1 and S2 are conjuncts
 S1S2 disjunction (or)
S1 and S2 are disjuncts
 S1S2 implication/conditional (if-then)
S1 is the antecedent/premise
S2 is the consequent/conclusion
 S1S2 equivalence/biconditional (if and only if)
19

20. Syntax of PL
 Models specify truth value for each proposition:
e.g. S1= true, S2= false
 Rules for evaluating truth with respect to model m
S is true iff S is false
S1S2 is true iff S1 is true and S2 is true
S1S2 is true iff S1 is true or S2 is true
S1S2 is true iff S1 is true or S2 is true
is true iff S1 is false or S2 is true
is false iff S1 is false and S2 is false
S1S2 is true iff S1S2 is true and S2S1 is true
 Operator Precedence: (highest)      (lowest)
20

21. Truth Tables
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
Given n symbols,
2n possible combinations of
truth value assignments.
here each row is an interpretation
21

22. Implication Truth Table
A B
false false
false true
true false
true true
AB
true
true
false
true
AB is equivalent to B A
B A
true
true
false
true
22

23. Validity
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
A sentence is valid
if it's true in all interpretations:
P1 P1 P1P1 (tautologies)
(i.e. its entire column is true)
A A
true
true
true
true
true
true
true
true
23

24. Satifiability
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
A sentence is satisfiable
if it's true in some interpretations:
P1 P2 P2P1
(i.e. its column is true and false)
A B
true
true
false
false
true
true
true
true
24

25. Unsatifiability
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
A sentence is unsatisfiable
if it's true in no interpretations:
P1 P1 (inconsistent/contradiction)
(i.e. its entire column is false)
C C
false
false
false
false
false
false
false
false
25

26. Inference Proof Methods
 Model Checking:
– truth table enumeration
sound and complete for propositional logic
– heuristic search in model space
sound but incomplete
 Application of Syntactic Operations
(i.e. Inference Rules):
– sound generation of new sentences from old
– could use inference rules as operators for search
26

27. Inference by Enumeration
LET: KB = AC, B C α = AB
DOES: KB ╞ α ?
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
RECALL: The computer
doesn't know the meaning
of the proposition symbols.
So all logically distinct cases
must be checked to prove that
a sentence can be derived
from a KB.
27

28. Inference by Enumeration
LET: KB = AC, B C α = AB
DOES: KB ╞ α ?
AC B C KB
false true false
true false false
false true false
true true true
true true true
true false false
true true true
true true true
Rows where all of
sentences in KB
are true are the
models of KB
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
28

29. Inference by Enumeration
LET: KB = AC, B C α = AB
DOES: KB ╞ α ?
AC B C KB
false true false
true false false
false true false
true true true
true true true
true false false
true true true
true true true
α is entailed by KB,
if all models of KB
are models of α,
i.e. all rows where
KB is true, α is true
A B C
false false false
false false true
false true false
false true true
true false false
true false true
true true false
true true true
AB
false
false
true
true
true
true
true
true
YES!
In other words:
KB α is valid.
KBα
true
true
true
true
true
true
true
true
29