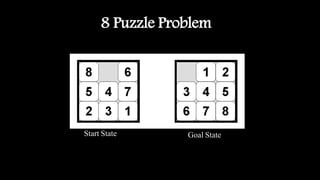
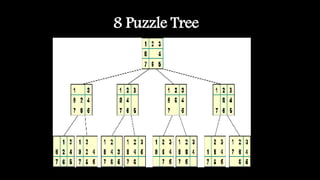
The document discusses various classical AI problems, including the water jug problem, the 8-queen problem, the 8-puzzle problem, and the missionaries and cannibals problem. It provides formulations for each problem, outlining state representations, production rules, and possible solutions. Each problem is aimed at demonstrating techniques in problem representation and search strategies within artificial intelligence.

1. AI Problem Representation
ARTIFICIAL INTELLIGENCE PART #6

2. Water Jug Problem
A Water Jug Problem: You are given two jugs, a 4-gallon
one and a 3-gallon one, a pump which has unlimited water
which you can use to fill the jug, and the ground on which
water may be poured. Neither jug has any measuring markings
on it. How can you get exactly 2 gallons of water in the 4-
gallon jug?

3. State Representation
 We will represent a state of the problem as a tuple
(x, y) where x represents the amount of water in the 4-
gallon jug and y represents the amount of water in the 3-
gallon jug.
 Initial state as (0,0).
 Goal state as (2,y).

4. Production Rules
1. (x,y) If x<4 -> (4,y)
2. (x,y) If y<3 ->(x,3)
3. (x,y) If x>0 ->(x-d,y)
4. (x,y) If y>0 ->(x,y-d)
5. (x,y) If x>0 ->(0,y)
6. (x,y) If y>0 ->(x,0)
7. (x,y) If (x+y>=4 and y>0) ->(4,y-(4-x))
8. (x,y) If (x+y>=3 and x>0) ->(x-(3-y),3)
9. (x,y) If(x+y<=4 and y>0) ->(x+y,0)
10.(x,y) If (x+y<=3 and x>0) ->(0,x+y)
11.(0,2) ->(2,0)

5. WATER JUG: one of the Solution
4 Gallon
Jug
3 Gallon
Jug
Rule
applied
0 0
4 0 1
1 3 8
1 0 6
0 1 10
4 1 1
2 3 8
4 Gallon jug 3 Gallon jug
pump

6. Search Tree : Water Jug Problem
(0,0)
(4,0)
(4,3) (0,0) (1,3)
(0,3)
(4,3) (0,0) (3,0)

7. 8 Queen Problem
Problem: Place 8 queens on a chess board so
that none of them attack each other.
Formulation- I
- A state is an arrangement of 0 to 8 queens on
the board
- Operators add a queen to any square.
This formulation is not a systematic way to
find the solution, it takes a long time to get
the solution.
-

8. Formulation – II
-A state is an arrangement of 0-8 queen with no one
attacked.
-Operators place a queen in the left most empty
column.
- More systematic than formulation-I
8 Queen Problem

9. Formulation –III
- A state is an arrangement of 8 queens on
in each column.
-Operators move an attacked queen to another
square in the same column.
-Keep on shuffling the queen until the goal is
reached.
- This formulation is more systematic hence ,
it is also called as Iterative Formulation.
8 Queen Problem

10. 8 Queen Problem: one solution

11. 8 Puzzle Problem
Start State Goal State

12. • State space (S)
• Location of each of the 8 tiles(and the blank tile)
• Start State (s)
• Starting configuration
Operators(O)
• Four Operators : Right, Left, Up, Down
• Goals(G) one of the goal configuration
8 Puzzle Problem

13. 8 Puzzle Tree

14. Missionaries and Cannibals
• Three missionaries and three cannibals find themselves on a side
of river. They agreed to get to the other side of river.
• But missionaries are afraid of being eaten by cannibals so, the
missionaries want to manage the trip in such a way that no. of
missionaries on either side of the river is never less than the no.
of cannibals on the same side.
• The boat is able to hold only 2 people at a time.

15. Missionaries and Cannibals:
State representation
• State(#m,#c,1/0)
#m – number of missionaries on first bank #c –
number of cannibals on first bank
• The last bit indicate whether the boat is in
the first bank.
Operators
• Boat carries (1,0) or (0,1) or (1,1) or (2,0) or
(0,2)

16. FIND SOLUTION ?