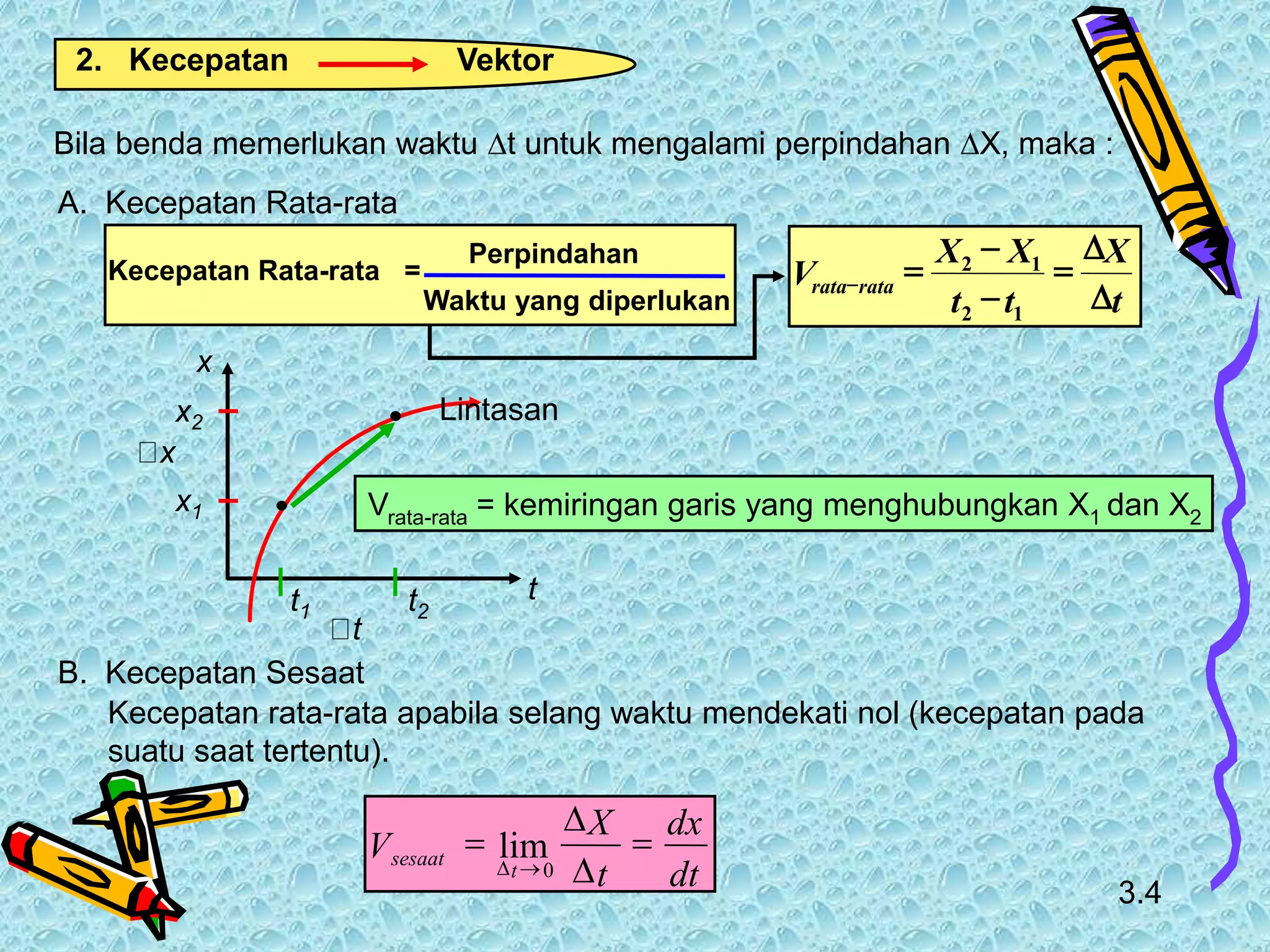
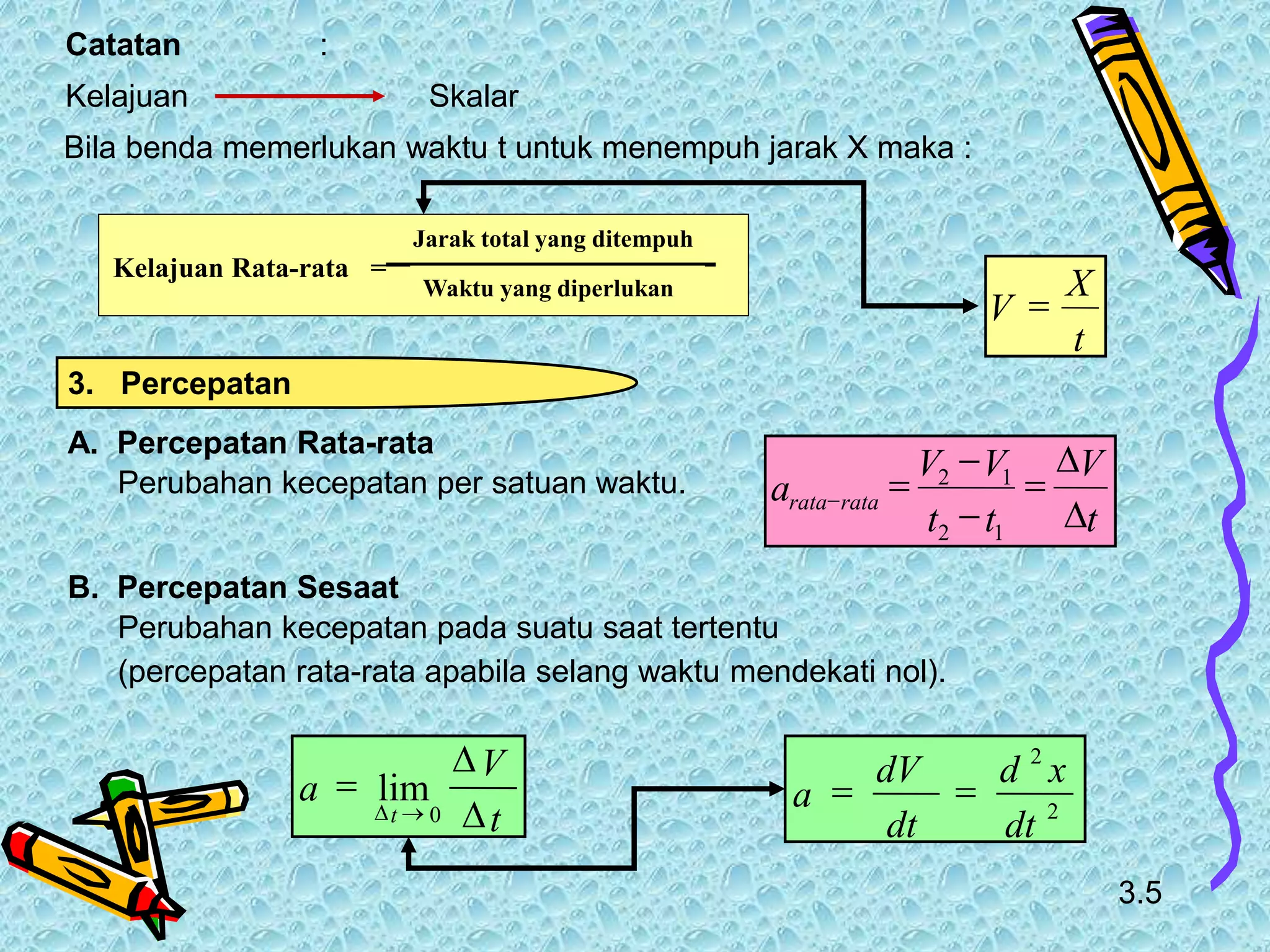
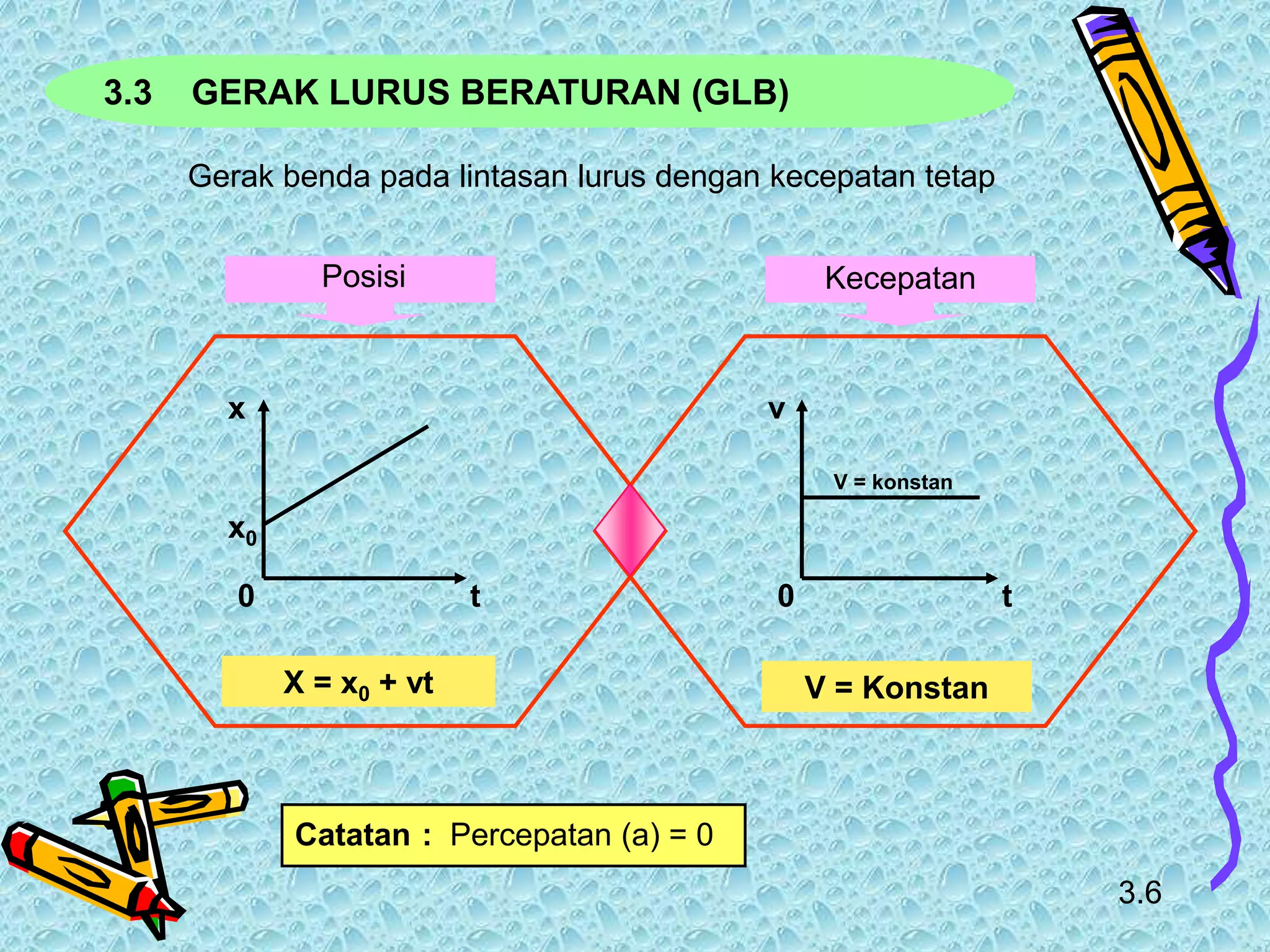
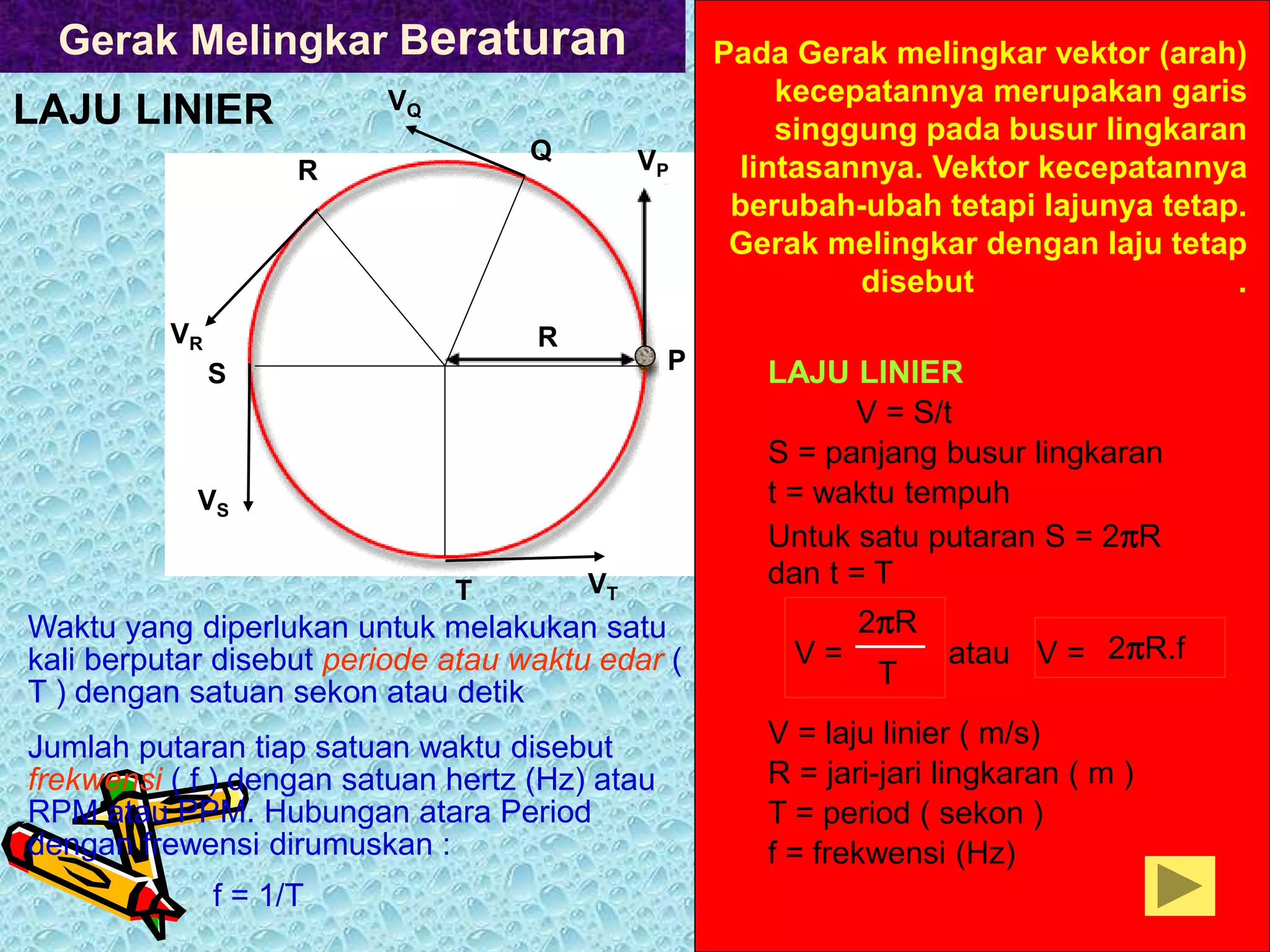
Dokumen tersebut membahas tentang kinematika gerak yang meliputi pengertian kinematika, jenis-jenis gerak yang dipelajari seperti gerak lurus dan melingkar, besaran-besaran fisika yang terkait seperti perpindahan, kecepatan dan percepatan, serta contoh soal terkait gerak lurus beraturan dan berubah beraturan.

1. KINEMATIKA GERAK
Drs. Agus Purnomo
aguspurnomosite.blogspot.com

2. Kinematika
• Mempelajari tentang gerak benda
tanpa memperhitungkan penyebab
gerak atau perubahan gerak.
• Asumsi bendanya sebagai benda titik
yaitu ukuran, bentuk, rotasi dan
getarannya diabaikan tetapi
massanya tidak(Sarojo, 2002)
• Pengertian dasar dari kinematika
benda titik adalah pengertian lintasan
hasil pengamatan gerak
• Keadaan gerak ditentukan oleh data
dari posisi (letak) pada setiap saat

3. Gerak yang Dipelajari
• Gerak 1 dimensi  lintasan berbentuk
garis lurus
Gerak lurus beraturan (GLB)
Gerak lurus berubah beraturan (GLBB)
Gerak lurus berubah tidak beraturan
• Gerak 2 dimensi  lintasan berada dalam
sebuah bidang datar
Gerak melingkar
Gerak parabola
• Gerak 3 dimensi  lintasan berada dalam
ruang (tidak dibahas)

4. GERAK LURUS
3.1

5. PENDAHULUAN
 Suatu benda dikatakan bergerak bila kedudukannya
selalu berubah terhadap suatu acuan
 Ilmu yang mempelajari gerak tanpa mempersoalkan
penyebabnya disebut Kinematika
 Untuk menghindari terjadinya kerumitan gerakan benda
dapat didekati dengan analogi gerak partikel (benda titik)
 Gerak lurus disebut juga sebagai gerak satu dimensi
3.2

6. Besaran Fisika dalam Studi
Kinematika
• Perpindahan (displacement)
• Kecepatan (velocity)
• Percepatan (accelaration)

7. 3.3
Perubahan kedudukan benda dalam selang waktu tertentu (tergantung sistem
koordinat).
Catatan:
Jarak Skalar
Panjang lintasan sesungguhnya yang ditempuh oleh benda
o B
A
perpindahan
X1 X2
X = X2 – X1
A B
5 m
5 m
Contoh :
Benda bergerak dari A ke B (5 m) dan
kembali lagi ke A
Perpindahan (X) = 0
Jarak = 5 m + 5 m = 10 m
PERPINDAHAN, KECEPATAN DAN PERCEPATAN
1. Perpindahan  Vektor

8. Bila benda memerlukan waktu t untuk mengalami perpindahan X, maka :
t
x
t1 t2
x
x1
x2 Lintasan
t
B. Kecepatan Sesaat
Kecepatan rata-rata apabila selang waktu mendekati nol (kecepatan pada
suatu saat tertentu).
3.4
Vrata-rata = kemiringan garis yang menghubungkan X1 dan X2
Kecepatan Rata-rata =
Perpindahan
Waktu yang diperlukan
2. Kecepatan Vektor
A. Kecepatan Rata-rata
dt
dx
t
X
V
t
sesaat
=


=

 0
lim
t
X
t
t
X
X
V rata
rata


=
-
-
=
-
1
2
1
2

9. 3.5
Catatan :
Kelajuan Skalar
Bila benda memerlukan waktu t untuk menempuh jarak X maka :
A. Percepatan Rata-rata
Perubahan kecepatan per satuan waktu.
B. Percepatan Sesaat
Perubahan kecepatan pada suatu saat tertentu
(percepatan rata-rata apabila selang waktu mendekati nol).
Kelajuan Rata-rata =
Jarak total yang ditempuh
Waktu yang diperlukan
3. Percepatan
t
V
t
t
V
V
a rata
rata


=
-
-
=
-
1
2
1
2
t
V
a
t 

=

 0
lim 2
2
dt
x
d
dt
dV
a =
=
t
X
V =

10. 3.3 GERAK LURUS BERATURAN (GLB)
Gerak benda pada lintasan lurus dengan kecepatan tetap
X = x0 + vt
0
x0
x
t
V = Konstan
0
V = konstan
v
t
3.6
Posisi Kecepatan
Catatan : Percepatan (a) = 0

11. GERAK LURUS BERATURAN
11
GLB = geral lurus beraturan adalah gerak
benda yang memiliki lintasan berupa garis
lurus dengan kecepatan tetap (baik besar
maupun arahnya)
t
S
v = vt
S = vt
X
X 
= 0
Dimana X0 = posisi awal benda

12. 3.7
3.4 GERAK LURUS BERUBAH BERATURAN (GLBB)
Gerak lurus yang percepatannya tidak berubah (tetap)
terhadap waktu  dipercepat beraturan
Percepatan
0
a = konstan
a
t
a = Konstan
x
t
x = x0 + v0t + ½ at2
Posisi
v
t
v = v0 + at
Kecepatan

13. 13
GLBB = gerak lurus berubah beraturan
adalah gerak benda yang memiliki lintasan
berupa garis dengan percepatan tetap.
Kecepatan :
Jarak
at
v
vt 
= 0
2
2
1
0 at
t
v
S 
=
aS
v
vt 2
2
0
2

=
GERAK LURUS BERUBAH BERATURAN

14.  Merupakan contoh dari gerak lurus berubah beraturan
 Percepatan yang digunakan untuk benda jatuh bebas adalah
percepatan gravitasi (biasanya g = 9,8 m/det2)
 Sumbu koordinat yang dipakai adalah sumbu y
3.8
 Hati-hati mengambil acuan
 Arah ke atas positif (+)
 Arah ke bawah negatif (-)
3.5 GERAK JATUH BEBAS
v2 = v0
2 - 2g (y – y0)
y = y0 + vot – ½ gt2
v = v0 - gt

15. 1. Sebuah mobil bergerak dengan kecepatan 27 km/jam, kemudian mobil dipercepat
dengan percepatan 2 m/s2.
Hitunglah kecepatan mobil dan jarak yang ditempuhnya selama 5 detik setelah percepatan
tersebut.
Jawab :
Vo = 27 km/jam = 27000 m /3600s = 7,5 m/s
Xo = 0, a = 2 m/s2, t = 5 s
- Kecepatan mobil
V = Vo +at
= 7,5 + 2,5
= 17,5 m/s
- Jarak yang ditempuh mobil
X = Xo + Vo.t + 1/2a.t 2
= 62,5 m
V = 17,5 m/s
Xo = 0 X = 62,5 m
Vo = 7,5 m/s
Contoh Soal
3.9

16. • Percepatan bola ketika meninggalkan pemain adalah
a = -g.
• Kecepatan pada ketinggian maksimum adalah V = 0
Jawab :
t = (V-Vo)/g = (0 - 12) / (-9,8) = 1.2 s
V = Vo + gt
Waktu untuk mencapai ketinggian maksimum :
Ketinggian maksimum yang dicapai :
2 . Seorang pemain baseball melempar bola sepanjang sumbu Y dengan kecepatan
awal 12 m/s. Berapa waktu yang dibutuhkan bola untuk mencapai ketinggian
maksimum dan berapa ketinggian maksimum yang dapat dicapai bola tersebut?
Y=0
Y = 7,3 m
( )
( ) m
3
,
7
=
m/s
9.8
-
2
m/s
12
-
0
=
a
2
v
-
v
=
y 2
2
2
o
4.0

18. R
VP
P
Q
R
S
T
VQ
VR
VS
VT
Pada Gerak melingkar vektor (arah)
kecepatannya merupakan garis
singgung pada busur lingkaran
lintasannya. Vektor kecepatannya
berubah-ubah tetapi lajunya tetap.
Gerak melingkar dengan laju tetap
disebut .
Jumlah putaran tiap satuan waktu disebut
frekwensi ( f ) dengan satuan hertz (Hz) atau
RPM atau PPM. Hubungan atara Period
dengan frewensi dirumuskan :
f = 1/T
Waktu yang diperlukan untuk melakukan satu
kali berputar disebut periode atau waktu edar (
T ) dengan satuan sekon atau detik
LAJU LINIER
V = S/t
S = panjang busur lingkaran
t = waktu tempuh
Untuk satu putaran S = 2pR
dan t = T
V = atau V =
V = laju linier ( m/s)
R = jari-jari lingkaran ( m )
T = period ( sekon )
f = frekwensi (Hz)
2pR
T
2pR.f
Gerak Melingkar Beraturan
LAJU LINIER

19. a
v
KECEPATAN SUDUT ( w )
q = w .t
q = lintasan sudut ( rad )
w = kecepatan sudut (rad/sekon = rad/s)
2 p = w .T
Untuk 1 periode
w =
2 p
T
w .= 2 p . f
KECEPATAN SUDUT ( w ) DENGAN
KECEPATAN LINIER ( V )
2p R
V =
T
V =
w
R

20. a
v Pada gerak melingkar beraturan benda
bergerak dengan lintasan berbentuk
lingkaran dengan jari-jari R. Selama
bergerak kecepatan (v) dan percepatan (a)
tetap tetapi arahnya berubah-berubah
ubah. Arah kecepatan selalu menyinggung
bidang lingkaran dan percepatan selalu
menuju ke pusat lingkaran sehingga
disebut percepatan sentripetal
Percepatan sentripetal dirumuskan
v2
a =
R
a = = w2 . R
w2 . R2
R
a =
4p2 .
R
T2
a = 4p2 .f2 .R
Benda yang bergerak melingkar beraturan mengalami
percepatan yang arahnya menuju ke pusat lingkaran,
besarnya sebanding dengan jari-jari lintasan dan
berbanding terbalik dengan kwadrat periodnya.

21. FS
Sebuah benda diikat dengan tali kemudian
diputar. Benda bergerak melingkar beraturan
dengan lintasan berbentuk lingkaran dengan
jari-jari R. Gerak benda ditahan oleh tali. Hal ini
berarti tali memberi gaya pada benda . Gaya ini
berasal dari gaya berat benda yang digantung .
Arah gaya sama dengan arah benang yaitu ke
pusat lingkaran dan disebut gaya sentripetal.
Menurut Hukum II Newton jika gaya
menimbulkan percepatan yang besarnya
sebanding dengan besar gaya yaitu :
FS = m.a
= m.(V2/R)
FS =
T = tegangan tali ( N )
FS = Gaya sentrifugal ( N )
m = massa benda ( kg )
a = percepatan sentripetal ( m/s2 )
R = jari-jari (m)
m .
4p2 .
R
T2

22. Sebuah benda bergerak melingkar
beraturan dengan jari-jari lintasan 50 cm
dan melakukan 6 putaran selama 3 menit.
Hitunglah :
a.Period putaran
b.Frekwensi putaran
c.Kecepatan sudut
d.Kecepatan linier
a
v
Penyelesaian :
Diketahui :
R = 50 cm = 0,5 m
n = 6 putaran
t = 3 menit
Ditanyakan :
a. T = ?
b. f = ?
c. w = ?
d. v = ?
Jawab :
a. T = t/n = 3/6 = ½ menit = 30 sekon
b. f = 1/T = 1/30 Hz
c. w = 2p . f = 2p . 1/30 = 1/15 p rad/s
d. v = w .R = 1/15p . 0,5 = 1/30 p m/s

23. Sebuah benda massanya 0,25 kg,
diikat pada ujung tali yang
panjangnya 0,5 m dan diputar
mendatar dengan 2 putaran tiap
sekon. Hitunglah :
a. Laju linier benda
b. Percepatan sentripetal benda
c. Gaya sentripetal pada benda
Penyelesaian :
Diketahui :
m = 0,25 kg ; R = 0,5 m ; f = 2 Hzt
Ditanyakan :
a. v = ?
b. aS = ?
c. FS = ?
Jawab :
a. v = 2p .R .f = 2p x 0,5 x 2 = 2p m/s
b. aS = = = 8 p2 m/s2
c. FS = m . aS = 0,25 x 8p2 = 2 p2 N
v2
R
(2p)2
0,5
as
Fs
v

24. Tiga roda A, B, dan C dirangkai seperti pada gambar. Masing-masing
berjari-jari 6 cm, 4 cm dan 8 cm. Roda A dan B dihubungkan dengan
rantai dan roda C seporos dengan roda B. Jika roda A berputar 2
putaran tiap detik, tentukan kecepatan linier roda C.
Penyelesaian :
Diketahui :
RA = 6 cm
RB = 4 cm
RC = 8 cm
fA = 2 Hz
Ditanyakan : vC = ?
Jawab :
Roda A: vA = 2p . RA. fA
= 2p x 6 x 2 = 24 p cm/s
Roda B : vB = vA
wB . RB = vA
wB = vA/ RB = 24 p / 4 = 6 p rad/s
Roda C : wC= wB = 6 p rad/s
vC = wC x RC = 6 p x 8 = 48 p cm/s
C
B
A
wB = wC
vA = vB

25. aguspurnomosite.blogspot.com
Kinematika Gerak