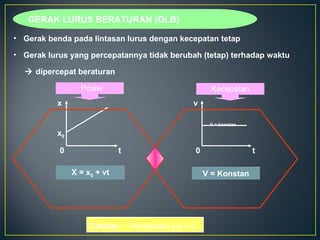
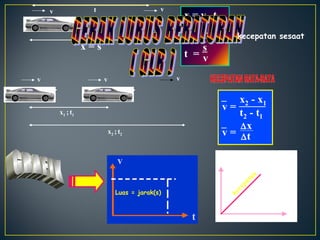
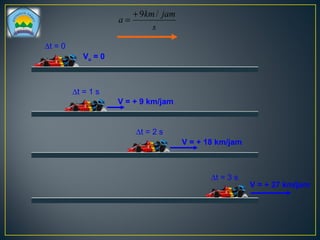
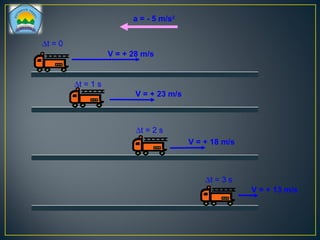
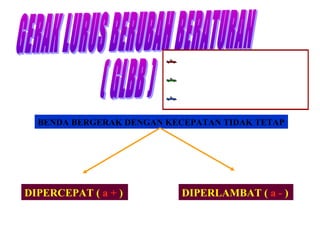
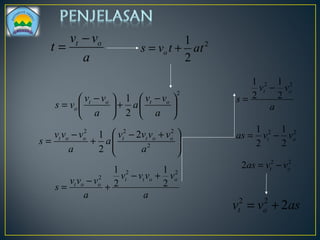
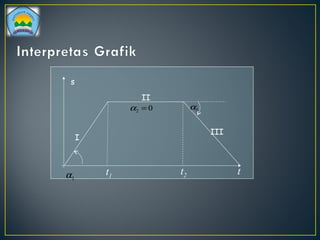
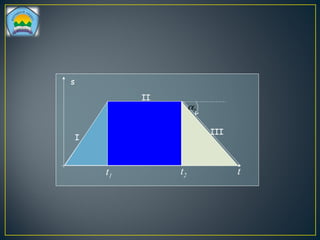
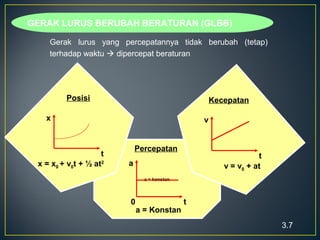
Dokumen ini membahas tentang gerakan benda, termasuk definisi gerak dan diam, jenis gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB), serta rumus-rumus yang digunakan untuk menghitung kecepatan, jarak, dan percepatan. Beberapa contoh soal juga disertakan untuk ilustrasi penerapan rumus dalam situasi nyata. Grafik yang menggambarkan hubungan jarak, kecepatan, dan percepatan juga disajikan untuk memperjelas konsep tersebut.

1. 1. DONI SINAGA1. DONI SINAGA
2. Adeli2. Adeli
3. MARTHALINA THERESIA3. MARTHALINA THERESIA
SITINJAKSITINJAK

3. • Suatu benda dikatakan bergerak apabila
kedudukan benda itu berubah posisinya.
• Suatu benda dikatakan diam (tidak bergerak)
apabila kedudukan benda itu tidak berubah dari
posisinya.

4. Menurut Definisi gerak, binatang mana yang
bergerak dan mana yang tidak bergerak.??

5. • Gerak benda yang lintasannya lurus.
• Gerak lurus suatu benda dalam kehidupan sehari-hari
umumnya tidak beraturan.
• Gerak lurus disebut juga sebagai gerak satu dimensi

6. GERAK LURUS BERATURAN (GLB)
• Gerak benda pada lintasan lurus dengan kecepatan tetap
• Gerak lurus yang percepatannya tidak berubah (tetap) terhadap waktu
 dipercepat beraturan
X = x0 + vt
0
x0
x
t
V = Konstan
0
V = konstan
v
t
Posisi Kecepatan
Catatan : Percepatan (a) = 0

7. v v
x = s
v v
x1 ;t1
x = vx t
v =
t =
s
t
s
v
x2 ;t2
v
x2 - x1
v =
v =
t2 - t1
∆x
∆t
t
v
t
Luas = jarak(s)
s
t
kecepatan
kecepatan sesaat

8. s
jamkm
a
/9+
=
∆t = 0
Vo = 0
∆t = 1 s
∆t = 2 s
∆t = 3 s
V = + 9 km/jam
V = + 18 km/jam
V = + 27 km/jam

9. a = - 5 m/s2
∆t = 0
∆t = 1 s
∆t = 2 s
∆t = 3 s
V = + 28 m/s
V = + 18 m/s
V = + 23 m/s
V = + 13 m/s

10. Grafik Jarak (s) – waktu (t) Grafik kecepatan(v) – waktu(t) Grafik percepatan(a) – waktu(t)
Jarak (s) kecepatan (v) Percepatan (a)
GRAFIK PADA GERAK LURUS BERATURAN (GLB)

11. BENDA BERGERAK DENGAN KECEPATAN TIDAK TETAP
DIPERCEPAT ( a + ) DIPERLAMBAT ( a - )

12. • Gerak benda pada lintasan lurus dengan
percepatan tetap
• Persamaan yang berlaku sebagai berikut:
t
vv
t
v
a ot −
=
∆
∆
=
tavv ot +=
2
2
1
tatvsos o ++=
savv ot 222
+=

13. a
vv
t ot −
= 2
2
1
tatvs o +=
2
2
1





 −
+




 −
=
a
vv
a
a
vv
vs otot
o





 +−
+
−
= 2
222
2
2
1
a
vvvv
a
a
vvv
s oottoot
a
vvvv
a
vvv
s
oott
oot
22
2
2
1
2
1
+−
+
−
=
a
vv
s
ot
22
2
1
2
1
−
=
22
2
1
2
1
ot vvas −=
22
2 ot vvas −=
asvv ot 222
+=

14. 1α
s
t
02 =α 3α
I
II
III
t1
t2

15. • Pada grafik di atas, kecepatan pada t, sama
dengan kemiringan grafik pada waktu t tersebut
αtan=v
• Dalam selang I, 0 < t < t1, sudut α1 positif, sehingga nilai v1
positif.
• Dalam selang II, t1 < t < t2, sudut α2 =0, sehingga nilai v2 =0.
• Dalam selang I, t3 < t < t3, sudut α3 negatif, sehingga nilai v3
negatif.
• Makin curam grafik, makin besar kelajuannya

16. s
t
1α
02 =α 3α
I
II
III
t1
t2

17. Jarak (s) kecepatan (v) Percepatan (a)
Jarak (s) – waktu (t) kecepatan (v) – waktu (t) percepatan (a) – waktu (t)
GRAFIK PADA GERAK LURUS BERUBAH BERATURAN (GLBB)
di Percepat ( a + )
X = Vo.t + ½ at2
V = Vo + at a = (V/Vo) : t
Vo2
= V2
+ 2a.s

18. Jarak (s) kecepatan (v) Percepatan (a)
Jarak (s) – waktu (t) kecepatan (v) – waktu (t) percepatan (a) – waktu (t)
GRAFIK PADA GERAK LURUS BERUBAH BERATURAN (GLBB)
di Perlambat ( a - )
X = Vo.t - ½ at2
V = Vo - at a = (V/Vo) : t
V2
= Vo2
- 2a.s

19. 3.7
GERAK LURUS BERUBAH BERATURAN (GLBB)
Gerak lurus yang percepatannya tidak berubah (tetap)
terhadap waktu  dipercepat beraturan
Percepatan
0
a = konstan
a
t
a = Konstan
x
t
x = x0 + v0t + ½ at2
Posisi
v
t
v = v0 + at
Kecepatan

20. Jawab :
Vo = 27 km/jam = 27000 m /3600s = 7,5 m/s
Xo = 0, a = 2 m/s2
, t = 5 s
- Kecepatan mobil
V = Vo +at
= 7,5 + 2,5
= 17,5 m/s
- Jarak yang ditempuh mobil
X = Xo + Vo.t + 1/2a.t 2
= 62,5 m
V = 17,5 m/s
Xo = 0 X = 62,5 m
Vo = 7,5 m/s
Contoh SoalContoh Soal
3.9

21. Seseorang mengendarai
sepeda motor, mula-mula
kecepatannya 18 km/jam,
setelah 10 sekon
kemudian kecepatannya
menjadi 54 km/jam.
Berapa percepatan sepeda
moto tersebut
Diketahui :
v1= 18 km/jam = 5 m/s
v2= 54 km/jam = 15 m/s
t = 10 s
Ditanyakan : a = ?
Jawab :
a =
=
v∆v
v∆v
v2-v1
v∆t
15 - 5
=
v10
= 1 m/s2
Seseorang mengendarai mobil dengan
kecepatan tetap 15 m/s. Tentukan :
a. Jarak yg ditempuh setelah 4 s,5 s.
b. Waktu yang diperlukan untuk me-
nempuh jarak 3 km
Diketahui :
v= 15 m/s
Ditanyakan :
a. s =…. ? (t = 4 s)
s =…. ? (t = 5 s)
b. t = …. ? ( s = 3 km = 3000 m )
s
Jawab :
Untuk t = 4 s
a. s = v x t
= 15 x 4 = 60 m
Untuk t = 5 s
s = v x t
= 15 x 5 = 75 m
b. t = =
= 200 s
v
3000
15
Sebuah benda bergerak ditunjukkan
seperti grafik diatas. Hitunglah jarak
yang ditempuh benda setelah berge-
rak selama a. 4 s b. 10 s c. 1 menit
4 10
5
t(s)
v (m/s)
0
Diketahui :
v= 5 m/s (kecepatan tetap)
Ditanyakan :
a. s =…. ? (t = 4 s)
b. s =…. ? (t = 10 s)
c. s = …. ? (t = 1 mnt=60 s )
Jawab :
Untuk t = 4 s
a. s = v x t
= 5 x 4 = 20 m
b. Untukt = 10 s
s = v x t
= 5 x 10 = 50 m
s = v x t = 5 x 60
= 300 m
c. Untuk t = 60 s 4 10
5
t(s)
v (m/s)
0 4 10
5
t(s)
v (m/s)
0
Luas =
jarak =
5 x 4 =
20
Luas =
jarak =
5 x 10 =
50

22. TERIMA KASIH