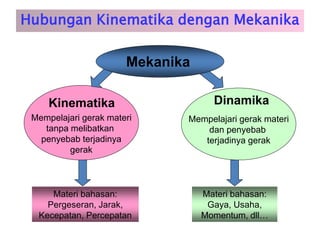
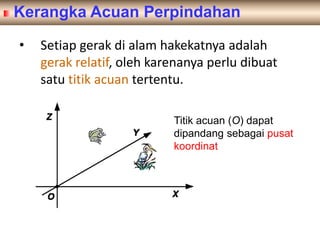
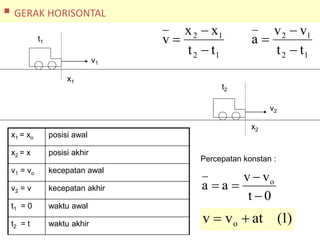
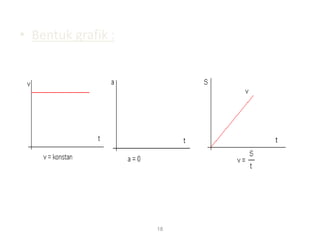
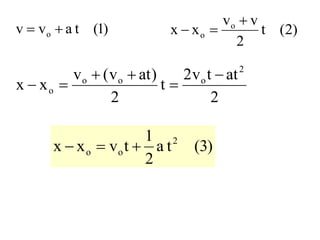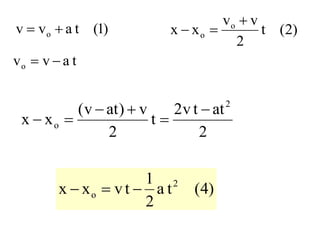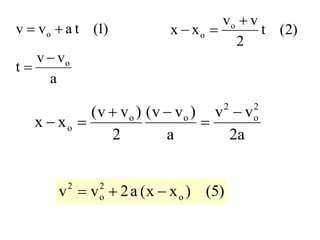Kinematika mempelajari gerak benda tanpa mempertimbangkan penyebabnya, sedangkan dinamika mempelajari gerak dan penyebabnya. Kinematika membahas konsep seperti percepatan, kecepatan, jarak, dan waktu untuk memahami gerak satu dan dua dimensi seperti gerak jatuh bebas, gerak parabola, dan gerak melingkar.

1. 1

2. Hubungan Kinematika dengan Mekanika
Mempelajari gerak materi
tanpa melibatkan
penyebab terjadinya
gerak
Kinematika
Mempelajari gerak materi
dan penyebab
terjadinya gerak
Dinamika
Mekanika
Materi bahasan:
Pergeseran, Jarak,
Kecepatan, Percepatan
Materi bahasan:
Gaya, Usaha,
Momentum, dll…

3. Kerangka Acuan Perpindahan
Kecepatan Sesaat dan Rata-rata
Percepatan
Gerak dengan Percepatan Konstan
Gerak Jatuh Bebas
Analisa Grafik dari Gerak

4. KINEMATIKA
 Kinematika adalah bidang ilmu fisika yang mempelajari tentang
gerak suatu obyek/benda tanpa memperhatikan penyebabnya
 KECEPATAN DAN PERCEPATAN RATA-RATA
• Bila suatu benda berubah posisinya (berpindah tempat) dalam
kurun waktu tertentu, maka benda tersebut dikatakan
mempunyai kecepatan
• Bila suatu benda berubah kecepatannya dalam kurun waktu
tertentu, maka benda tersebut dikatakan mempunyai percepatan
t
v
tt
vv
a
t
x
tt
xx
v
12
12
12
12












x1 = posisi awal
x2 = posisi akhir
v1 = kecepatan awal
v2 = kecepatan akhir
t1 = waktu awal
t2 = waktu akhir

5.  GERAK SATU DIMENSI
 Gerak Horisontal
 Gerak Vertikal (Jatuh Bebas)
 GERAK DUA DIMENSI
 Gerak Parabola (Peluru)
 Gerak Melingkar
 Gerak Relatip
 GERAK DENGAN PERCEPATAN KONSTAN

6. • Setiap gerak di alam hakekatnya adalah
gerak relatif, oleh karenanya perlu dibuat
satu titik acuan tertentu.
Kerangka Acuan Perpindahan
Titik acuan (O) dapat
dipandang sebagai pusat
koordinat

7. Kecepatan Rata-rata adalah rate pergeseran dalam
selang waktu tertentu:
Kelajuan adalah Jarak yang ditempuh dalam selang
waktu tertentu:
v : kecepatan
r : rate pergeseran
t : selang waktu
Diperoleh dengan mengambil limit Δt  0.
t
r
tt
rr
vr






12
12
t
r
tt
rr
v
ttt
s






 0
12
12
limlim
12

8. 8
Pesawat sedang melakukan gerak satu dimensi

9. 9
Mobil di jalan tol sedang melakukan gerak satu dimensi

10. 10
Kereta api sedang melakukan gerak satu dimensi

11. Gerak satu dimensi:
Posisi benda dinyatakan secara lengkap
dengan satu variabel saja
jyixr ˆˆ 

kzjyixr ˆˆˆ 

ixr ˆ

jyr ˆ

Untuk gerak dua dimensi dan tiga dimensi,
variabel posisi lebih dari satu
Dua Dimensi
Tiga Dimensi
11
Selanjutnya simbol
vektor dapat dibuang

12.  GERAK HORISONTAL
12
12
12
12
tt
vv
a
tt
xx
v






x1
x2
v1
v2
t1
t2
x1 = xo posisi awal
x2 = x posisi akhir
v1 = vo kecepatan awal
v2 = v kecepatan akhir
t1 = 0 waktu awal
t2 = t waktu akhir
Percepatan konstan :
0t
vv
aa o



)1(atvv o 

13. x1 = xo posisi awal
x2 = x posisi akhir
v1 = vo kecepatan awal
v2 = v kecepatan akhir
t1 = 0 waktu awal
t2 = t waktu akhir
2
vv
v o 

0t
xx
tt
xx
v o
12
12






Kecepatan rata-rata :
0t
xx
2
vv oo




)2(t
2
vv
xx o
o



14. )1(tavv o  )2(t
2
vv
xx o
o


2
attv2
t
2
)atv(v
xx
2
ooo
o




)3(ta
2
1
tvxx 2
oo 

15. )1(tavv o  )2(t
2
vv
xx o
o


2
attv2
t
2
v)atv(
xx
2
o




)4(ta
2
1
tvxx 2
o 
tavvo 

16. )1(tavv o  )2(t
2
vv
xx o
o


a2
vv
a
)vv(
2
)vv(
xx
2
o
2
oo
o




)5()xx(a2vv o
2
o
2

a
vv
t o


17. tavv)1( o 
t
2
vv
xx)2( o
o


2
oo ta
2
1
tvxx)3( 
2
o ta
2
1
tvxx)4( 
)xx(a2vv)5( o
2
o
2

5 buah persamaan dengan 4 variabel

18. 18
• Bentuk grafik :

19. Sebuah pesawat jumbo jet memerlukan kecepatan minimum sebesar 360
km/jam agar dapat tinggal landas. Panjang landas pacu yang ada di bandar
udara adalah 2000 m.
a) Berapa waktu yang diperlukan sebelum tinggal landas ?
b) Berapa percepatan minimum yang harus dihasilkan oleh mesin
jumbo jet tersebut.
Jawab :
s
m
100
s3600
m1000
360
jam
km
360vm2000xx0v oo 
a). Untuk menghitung percepatan gunakan persamaan (5) :
2
2
o
2
o
2
o
2
o
2
s
m
5,2
)2000(2
0100
)xx(2
vv
a
)xx(a2vv







Variabel yang sudah diketahui 3 :

20. Penerapan GLBB
• Gerak Jatuh Bebas (GJB)
• Gerak Vertikal ke Bawah (GVB)
• Gerak Vertikal ke Atas (GVA)

21. tavv)1( o 
t
2
vv
xx)2( o
o


2
oo ta
2
1
tvxx)3( 
2
o ta
2
1
tvxx)4( 
)xx(a2vv)5( o
2
o
2

5 buah persamaan dengan 4 variabel

22. Gerak Jatuh Bebas (GJB)
• Benda dijatuhkan dari suatu ketinggian tanpa
kecepatan awal (v0 = 0) dan selama geraknya
mengalami percepatan tetap (g = 9,8 m/s2 =
10 m/s2 ).
• v0 = 0
• a = g
• x-xo = h

23. Gerak Vertikal ke Bawah (GVB)
• Gerak suatu benda yang dilempar tegak lurus
ke bawah dengan kecepatan awal (v0  0)
• v0  0
• a = g
• x-xo = h

24. Gerak Vertikal ke Atas (GVA)
• Gerak suatu benda yang dilempar tegak lurus
ke atas dengan kecepatan awal tertentu (v0 
0).
• v0  0
• a = - g
• x-xo = h

25. Tugas
• Carilah persamaan ketiga gerak tersebut
dengan ciri-ciri atau syarat yang sudah
ditentukan!!
25

26. • Soal: Sebuah bola dijatuhkan dari suatu ketinggian.
Tentukan kedudukan dan kelajuan bola setelah
bergerak selama 5 s.
• Soal: seorang anak melempar batu ke dalam sumur
dengan kecepatan awal 3 m/s. Anak itu mendengar
bunyi batu mengenai dasar sumur setelah 2 sekon.
Tentukan kecepatan batu dan kedalaman sumur.
• Soal: sebuah kembang api diluncurkan vertikal ke
atas dengan kecepatan awal 20 m/s. 1 detik
kemudian kembang api tersebut memancar.
Tentukan kecepatan dan ketinggian akhir kembang
api saat memancar.
26