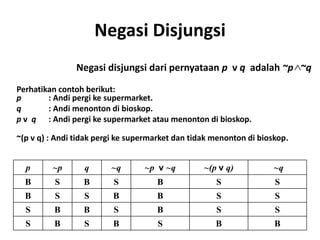
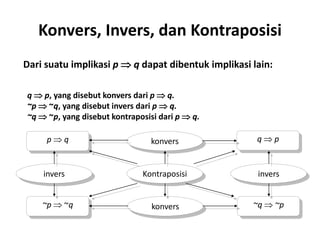
Dokumen tersebut membahas tentang logika matematika. Secara singkat, dokumen tersebut menjelaskan tentang pengertian pernyataan, lambang dan nilai kebenaran suatu pernyataan, pernyataan majemuk seperti disjungsi, konjungsi, implikasi dan biimplikasi, serta kuantor universal dan eksistensial.