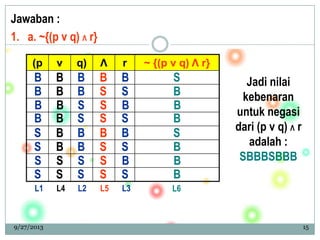
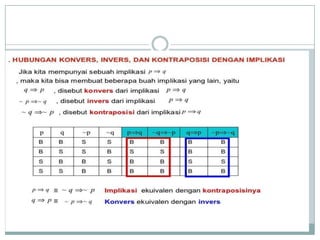
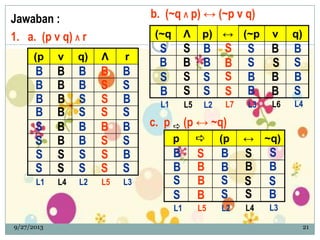
Dokumen ini membahas konsep logika proposisional, termasuk nilai kebenaran, kontradiksi, kontingensi, dan ekuivalensi pernyataan majemuk. Terdapat contoh penerapan biimplikasi dan sifat-sifat logika seperti komutatif, asosiatif, dan distributif. Selain itu, dokumen juga mencakup latihan untuk menentukan nilai kebenaran serta invers, konvers, dan kontraposisi dari berbagai pernyataan.

2. •

4. Contoh :
Tentukan Nilai kebenaran dari p => (p v q)
p q P v q P => (p v q)

5. Kontradiksi
Pernyataan majemuk yang semua kemungkinan nilai
kebenarannya selalu bernilai salah

6. 3. Kontingensi
Pernyataan majemuk yang semua kemngkinan nilai
kebenarannya bernilai benar atau salah.

7. Contoh:
 Tentukan nilai kebenaran (p V ~q) => ~r
p q r ~q ~ r (pV ~q) (pV ~q)=> ~q

9. Ekuivalen

10. Dua buah pernyataan majemuk yang
ekuivalen
 Untuk memahami pengartian dua buah pernyataan
majemuk yang ekuivalen, perhatikan dua buah
pernyaan berikut :
a = (p v q ) dan b = ( q v p )
 Dari pernyataan a dan b itu dapat dibentuk
biimplikasi.
a <=> b atau (p v q) <=> (q v p)
 Nilai kebenaran biimplikasi (p v q) <=> (q v p)

11. Secara umum dapat disimpulkan :
 Tautologi yang berbentuk a <=> b dinamakan
ekuivalen logis dan dituliskan dengan lambang a Ξ
b.
 Dua buah pernyataan majemuk dikatakan
ekuivalen, jika kedua pernyataan majemuk itu
mempunyai nilai kebenaran yang sama untuk
semua kemungkinan nilai kebenaran pernyataan –
pernyataan komponennya.

12.  Sifat komutatif
a) p v q Ξ q v p
b) p q Ξ q p .................. (4-2)
 Sifat asosiatif
a. (p v q) v r Ξ p v (q v r)
b. (p q) r Ξ p (q r) ..................(4-3)
 Sifat distributif
a) Distributif disjungsi terhadap konjungsi.
p v (q r) Ξ (p v q) (p v r)
b) Distributif konjungsi terhadap dijungsi.
p (q v r) Ξ (p q) v (p r) ............(4-4)

14. Latihan 2.
1. Carilah nilai kebenaran untuk negasi dari (p v q) Λ r
dengan tabel kebenaran
2. Tentukanlah negasi dari pernyataan berikut :
a. p : Jika Jaka siswa SMA, maka ia lulusan SMP
b. p : Jika x = 3, maka x2 = 9
c. p : Jika x – 1 > 0, maka x2 – 5x + 4 > 0
d. p : Semua ayam berbulu hitam
e. p : Ada beberapa persamaan kuadrat mempunyai
akar imajiner
14

15. Jawaban :
1. a. ~{(p v q) Λ r}
9/27/2013 15
S
B
B
B
S
B
B
B
L6
Jadi nilai
kebenaran
untuk negasi
dari (p v q) Λ r
adalah :
SBBBSBBB
(p v q) Λ r ~ {(p v q) Λ r}
B
S
B
S
B
S
B
S
B
S
S
B
B
S
S
B
B
B
B
B
S
S
S
S
B
B
B
B
B
S
B
S
B
S
S
S
B
S
S
S
L2 L3L1 L4 L5

16. 9/27/2013 16
2. a. p : Jika Jaka siswa SMA, maka ia lulusan SMP
~p : Jika Jaka bukan siswa SMA, maka ia bukan lulusan
SMP
b. p : Jika x = 3, maka x2 = 9
~p : Jika x ≠ 3, maka x2 ≠ 9
c. p : Jika x – 1 > 0, maka x2 – 5x + 4 > 0
~p : Jika x – 1 ≤ 0, maka x – 5x + 4 ≤ 0
d. p : Semua ayam berbulu hitam
~p : Ada beberapa ayam yang berbulu hitam
e. p : Ada beberapa persamaan kuadrat mempunyai
akar imajiner
~p : Semua persamaan kuadrat mempunyai akar imajiner

17. D. Konvers, Invers, dan Kontraposisi
Dari implikasi p q dapat dibentuk implikasi baru :
 q → p disebut konvers dari implikasi semula
 ~ p → ~ q disebut invers dari implikasi semula
 ~ q → ~ p disebut kontraposisi dari implikasi
semula

19. Contoh :
p : Tia penyanyi
q : Tia seniman
 implikasi p → q : Jika Tia penyanyi maka Tia seniman
 Konvers q → p : Jika Tia seniman maka Tia penyanyi
 Invers ~ p → ~ q : Jika Tia bukan penyanyi maka Tia
bukan seniman
 Kontraposisi ~ q → ~ p : Jika Tia bukan seniman maka
Tia bukan penyanyi

20. Latihan 1.
1. Carilah nilai kebenaran pernyataan berikut dengan tabel
kebenaran
a. (p v q) Λ r
b. (~q Λ p) ↔ (~p v q)
c. p → (p ↔ ~q)
2. Tentukanlah Invers, Konvers dan Kontraposisi dari
pernyataan berikut :
a. Jika Jaka siswa SMA, maka ia lulusan SMP
b. Jika x = 3, maka x2 = 9
c. Jika x – 1 > 0, maka x2 – 5x + 4 > 0
9/27/2013 20

21. Jawaban :
1. a. (p v q) Λ r
9/27/2013 21
(p v q) Λ r
b. (~q Λ p) ↔ (~p v q)
(~q Λ p) ↔ (~p v q)
c. p  (p ↔ ~q)
p  (p ↔ ~q)
B
S
S
B
B
S
S
B
B
S
B
BS
S B
B
S
B
S
B
B
S
S
S
B
S
S
S
B
S
B
S
B
S
B
S
B
S
S
B
B
S
S
B
B
B
B
B
S
S
S
S
B
B
B
B
B
S
B
S
B
S
S
S
B
S
S
S B
B
S
S
B
B
S
S S
B
S
B
S
S
B
S
S
B
B
B
L4L6L2 L3L1 L5 L7
L2 L3L1 L4 L5
L1 L2 L3L4L5

22. 2. a. Jika Jaka siswa SMA, maka ia lulusan SMP
Invers : Jika Jaka bukan siswa SMA, maka ia bukan
lulusan SMP
Konvers : Jika Jaka lulusan SMP, maka ia siswa SMA
Kontraposisi : Jika Jaka bukan lulusan SMP, maka ia bukan
siswa SMA
b. Jika x = 3, maka x2 = 9
Invers : Jika x ≠ 3, maka x2 ≠ 9
Konvers : Jika x2 = 9, maka x = 3
Kontraposisi : Jika x2 ≠ 9, maka x ≠ 3
c. Jika x – 1 > 0, maka x2 – 5x + 4 > 0
Invers : Jika x – 1 ≤ 0, maka x – 5x + 4 ≤ 0
Konvers : Jika x – 5x + 4 > 0, maka x – 1 > 0
Kontraposisi : Jika x – 5x + 4 ≤ 0, maka x – 1 ≤ 0
9/27/2013 22