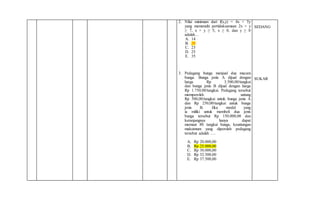
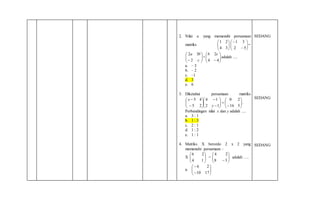
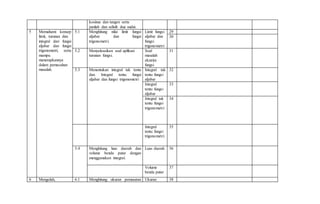
1. Dokumen tersebut berisi kisi-kisi soal UN Matematika SMA program IPA tahun 2016 berdasarkan UN 2015. Terdapat 12 standar kompetensi dan butir soalnya. 2. Materi yang diujikan meliputi logika matematika, aturan pangkat dan akar, persamaan kuadrat, sistem persamaan linear, persamaan lingkaran dan garis singgungnya, teorema sisa dan faktor, serta program linear. 3. Soal-soal bervariasi dari mudah h

1. PREDIKSI SOAL UN 2016 BERDASARKAN KISI-KISI UN 2015
Tingkat Satuan Pendidikan : SMA
Mata Pelajaran : MATEMATIKA
Program : IPA Penulis : KELOMPOK 2
Kurikulum : KTSP/2013
NO.
SKL
STANDAR
KOMPETENSI
LULUSAN
NO.
IKL
INDIKATOR
KOMPETENSI
LULUSAN
MATERI
No
Soal BUTIR SOAL
Tingkat
Kesukaran
Soal
1 Menggunakan
logika matematika
dalam pemecahan
masalah
1.1 Menentukan penarikan
kesimpulan dari
beberapa premis.
Penarikan
kesimpulan
1
1.2 Menentukan ingkaran
atau kesetaraan dari
pernyataan majemuk
atau pernyataan
berkuantor.
Ingkaran dari
Pernyataan
majemuk
2
2 Menyelesaikan
masalah yang
berkaitan dengan
aturan pangkat,
akar
dan logaritma,
fungsi aljabar
sederhana, fungsi
kuadrat,
fungsieksponen
dan grafiknya,
fungsi
komposisi dan
fungsi invers,
sistem
2.1 Menggunakan aturan
pangkat, akar, dan
logaritma.
Bentuk
pangkat
3
Bentuk akar 4

2. persamaan linear,
persamaan dan
pertidaksamaan
kuadrat,
persamaan
lingkaran dan garis
singgungnya, suku
banyak, algoritma
sisa dan teorema
pembagian,
program linear,
matriks dan
determinan,
vektor,
transformasi
geometri dan
komposisinya,
barisan dan deret,
serta
mampu
menggunakannya
dalam pemecahan
masalah.
Bentuk
logaritma
5
2.2 Menggunakan rumus
jumlah dan hasil kali
akar-akar persamaan
kuadrat.
Menyusun
persamaan
kuadrat
6
2.3 Menyelesaikan masalah
persamaan atau fungsi
kuadrat dengan
menggunakan
diskriminan.
Jenis akar-
akar
persamaan
kuadrat
7
2.4 Menyelesaikan masalah sehari- Penerapan 8

3. hari yang berkaitan dengan
sistem persamaan linear.
Sistem
Persamaan
Linear Dua
dan Tiga
Variabel
2.5 Menentukan persamaan
lingkaran atau garis singgung
lingkaran.
Persamaan
Lingkaran
9 1. Persamaan lingkaran yang berpusat
(0,0) dan berjari-jari
1
√6
adalah….
A. 𝑥2
+ 𝑦2
= 6
B. 𝑥2
+ 𝑦2
= √6
C. 𝑥2
+ 𝑦2
=
1
6
D. 𝑥2
+ 𝑦2
+ 6𝑥 + 6𝑦 = 6
E. 𝑥2
+ 𝑦2
+ 6𝑥 + 6𝑦 = 36
2. Persamaan lingkaran yang berpusat
(3,4) dan berjari-jari 6 adalah….
A. 𝑥2
+ 𝑦2
+ 6𝑥 + 8𝑦 + 11 = 0
B. 𝑥2
+ 𝑦2
+ 8𝑥 + 6𝑦 + 11 = 0
C. 𝑥2
+ 𝑦2
+ 6𝑥 − 8𝑦 − 11 = 0
D. 𝑥2
+ 𝑦2
− 8𝑥 − 6𝑦 − 11 = 0
E. 𝑥2
+ 𝑦2
− 6𝑥 − 8𝑦 − 11 = 0
3. Pusat lingkaran 𝑥2
+ 𝑦2
+ 4𝑥 − 6𝑦 +
13 = 0 adalah….
A. (-2,3)
B. (2,-3)
C. (-2,-3)
D. (2,3)
E. (4,6)
MUDAH
SEDANG
SEDANG

4. 4. Persamaan lingkaran yang berpusat
(2,3) dan melalui titik (5,-1) !
A. 𝑥2
+ 𝑦2
− 4𝑥 − 𝑦 − 12 = 0
B. 𝑥2
+ 𝑦2
− 4𝑥 + 6𝑦 − 12 = 0
C. 𝑥2
+ 𝑦2
+ 6𝑥 − 4𝑦 − 12 = 0
D. 𝑥2
+ 𝑦2
− 8𝑥 − 4𝑦 − 12 = 0
E. 𝑥2
+ 𝑦2
− 4𝑥 − 8𝑦 − 12 = 0
5. Diketahui titik A(5,-1) dan B(2,4).
Persamaan lingkaran yang diameternya
melalui titik A dan B adalah….
A. 𝑥2
+ 𝑦2
+ 6𝑥 + 8𝑦 + 6 = 0
B. 𝑥2
+ 𝑦2
+ 8𝑥 + 6𝑦 + 11 = 0
C. 𝑥2
+ 𝑦2
+ 7𝑥 − 3𝑦 − 6 = 0
D. 𝑥2
+ 𝑦2
− 7𝑥 − 3𝑦 + 6 = 0
E. 𝑥2
+ 𝑦2
+ 7𝑥 − 8𝑦 − 6 = 0
SUKAR
SUKAR
Persamaan
garis
singgung
lingkaran
10
1. Nilai a memenuhi agar garis y = x + a
menyinggung lingkaran
𝑥2
+ 𝑦2
− 6𝑥 − 2𝑦 + 2 = 0 adalah….
A. -6 atau 2
B. 2 atau 6
C. -6 atau -2
SEDANG

5. D. -2 atau 6
E. 1 atau 2
2. Salah satu persamaan garis singgung L
= x2 + y2 — 10x + 14y + 49 = 0 di titik
yang berabsis 1,
adalah ….
A. 4x - 3y - 21 = 0
B. 4x + 3y - 21 = 0
C. 4x - 3y + 21 = 0
D. 3x - 2y - 18 = 0
E. 3x + 2y - 18 = 0
3. Lingkaran x2 + y2 — 16x – 12y = 0
memotong sumbu Y di titik P. salah
satu persamaan garis singgung
lingkaran di titik P adalah….
A. 𝑦 =
4
3
𝑥 + 12
B. 𝑦 = −
4
3
𝑥 + 12
C. 𝑦 =
3
4
𝑥 + 9
D. 𝑦 =
3
4
𝑥 + 12
E. 𝑦 = −
3
4
𝑥 + 12
SEDANG
SUKAR

6. 4. Persamaan garis singgung
x2 + y2 — 4x + 6y -12 = 0 di titik (5,1)
adalah ...
A. 4x - 3y - 21 = 0
B. 3x + 4y - 19 = 0
C. 4x - 3y + 21 = 0
D. 3x - 2y - 19 = 0
E. 3x -4y - 19 = 0
5. Garis singgung lingkaran 𝑥2
+ 𝑦2
=
25 di titik (-3,4) menyinggung
lingkaran dengan pusat (10,5). maka
jari-jari yang berpusat di (10,5)
adalah….
A. 16
B. 10
C. 7
D. 6
E. 4
MUDAH
SUKAR
2.6 Menyelesaikan masalah yang
berkaitan dengan teorema sisa
atau teorema faktor.
Teorema
sisa
11
1. Sisa pembagian suku banyak ( x4 – 4x3
+ 3x2 – 2x + 1 ) oleh ( x2 – x – 2 )
adalah ….
A. –6x + 5
B. –6x – 5
C. 6x + 5
MUDAH

7. D. 6x – 5
E. 6x – 6
2. Jika suku banyak P(x) = 2x4 + ax3 –
3x2 + 5x + b dibagi oleh ( x2 – 1 )
memberi sisa 6x + 5, maka a.b = ….
A. – 6 B.3 C.1 D.6 E. 8
3. Diketahui suku banyak f(x) jika dibagi
( x + 1) sisanya 8 dan dibagi ( x – 3 )
sisanya 4. Suku banyak q(x) jika dibagi
dengan ( x + 1 ) bersisa –9 dan jika
dibagi ( x – 3 ) sisanya 15 . Jika h(x) =
f(x).q(x), maka sisa pembagian h(x)
oleh x2 – 2x – 3 sisanya adalah ….
A. –x + 7
B. 6x – 3
C. –6x – 21
D. 11x – 13
E. 33x – 39
4. Suku banyak P(x) = 3x3 – 4x2 – 6x + k
habis dibagi ( x – 2 ). Sisa pembagian
SEDANG
SUKAR
SEDANG

8. P(x) oleh x2 + 2x + 2 adalah ….
A. 20x + 24
B. 20x – 16
C. 32x + 24
D. 8x + 24
E. –32x – 16
5. Jika f(x) dibagi ( x – 2 ) sisanya 24,
sedagkan jika f(x) dibagi dengan ( 2x –
3 ) sisanya 20. Jika f(x) dibagi dengan (
x – 2 ) ( 2x – 3 ) sisanya adalah ….
A. 8x + 8
B. 8x – 8
C. – 8x + 8
D. – 8x – 8
E. – 8x + 6
SUKAR
Teorema
faktor
12 1. Suku banyak f(x) = 6x3 + 13 x2 + q x +
12 mempunyai faktor (3x -1) , Faktor
linier yang lain adalah...
A. 2x -1 D. x + 4
B. 2x + 3 E. x + 2
C. x - 4
MUDAH

9. 2. Diketahui ( x + 1 ) salah satu factor dari
suku banyak f(x) = 2x4 – 2x3 + px2 – x
– 2, salah satu factor yang lain adalah
….
A. x – 2
B. x + 2
C. x – 1
D. x – 3
E. x + 3
3. Salah satu faktor suku banyak
P(x) = x3 – 11x2 + 30x – 8 adalah …
A. (x + 1)
B. (x – 1)
C. (x – 2)
D. (x – 4)
E. (x – 8)
4. Diketahui (x – 2) dan (x – 1) adalah
factor–faktor suku banyak P(x) = x3 +
ax2 –13x + b. Jika akar–akar persamaan
suku banyak tersebut adalah x1, x2, x3,
untuk x1> x2> x3 maka nilai x1 – x2 – x3
= …
A. 8
B. 6
C. 3
D. 2
E. –4
SEDANG
SEDANG
SUKAR

10. 5. Suku banyak (2x3 + ax2 – bx + 3)
dibagi oleh (x2 – 4) bersisa (x + 23).
Nilai a + b = …
A. –1
B. –2
C. 2
D. 9
E. 12
SUKAR
2.7 Menyelesaikan masalah yang
berkaitan dengan komposisi
dua fungsi atau fungsi invers.
Fungsi
komposisi
13 .
1. Diketahui fungsi f : R  R, dan g : R
 R, dengan f(x) = x + 3 dan g(x) =
x2 – 2. Rumus (gof)(x) adalah....
A. x2 + 2x + 3
B. x2 + 3x + 3
C. x2 + 6x + 7
D. x2 + 8x + 9
E. x2 + 8x + 15
2. Diketahui fungsi f dan g yang
dirumuskan oleh f(x) = 3x2 – 4x + 6
dan g(x) = 2x –1. Jika nilai (fog)(x) =
101 maka nilai x yang memenuhi
adalah….
a.
3
2
3 dan –2
b.
3
2
3 dan 2
c.
11
3
dan 2
MUDAH
SEDANG

11. d.
3
2
3 dan –2
e.
11
3
 dan –2
3. Dari fungsi f : R  R dan g : R  R
diketahui bahwa f(x) = 2x - 3 dan
(gof) (x) = 4x2 – 16 x + 18, maka g
ditentukan oleh g(x) =……
a. x2 – 5x – 6
b. x2 – 8x – 15
c. x2 – 14x – 33
d. x2 – 14x + 24
e. x2 – 2x + 3
4. Jika f(x) = 3x maka f -1(x) =….
a.
x3
1
b. 3
1

x
c. (x – 3)2
d. 2
)3(
1
x
e. 2
)3(
1
x
5. Jika f(x) =
x
1
dan g(x) = 2x – 1 ,
maka (f o g) –1 (x) = …….
SEDANG
SEDANG
SUKAR

12. a.
x
x 12 
b.
12 x
x
c.
x
x
2
1
d.
1
2
x
x
e.
x
x
2
12 
2.8 Menyelesaikan masalah
program linear.
Model
matematika
dan Solusi
program
linear
14
1. Sistem pertidaksamaan linear dari
daerah yang diarsir pada gambar
adalah….
A. x + 2y ≥ 4; 3x+2y ≤ 6; x ≥ 0; y ≥ 0
B. x – 2y ≤ 4; 3x+2y ≤ 6; x ≥ 0; y ≥ 0
C. x + 2y ≤ 4; 3x – 2y ≤ 6; x ≥ 0; y ≥ 0
D. x + 2y ≥ 4; 3x+2y ≥ 6; x ≥ 0; y ≥ 0
E. x + 2y ≤ 4; 3x+2y ≤ 6; x ≥ 0; y ≥ 0
MUDAH

13. 2. Nilai minimum dari f(x,y) = 4x + 5y
yang memenuhi pertidaksamaan 2x + y
≥ 7, x + y ≥ 5, x ≥ 0, dan y ≥ 0
adalah…
A. 14
B. 20
C. 23
D. 25
E. 35
3. Pedagang bunga menjual dua macam
bunga. Bunga jenis A dijual dengan
harga Rp 3.500,00/tangkai
dan bunga jenis B dijual dengan harga
Rp 1.750,00/tangkai. Pedagang tersebut
memperoleh untung
Rp 500,00/tangkai untuk bunga jenis A
dan Rp 250,00/tangkai untuk bunga
jenis B. Jika modal yang
ia miliki untuk membeli dua jenis
bunga tersebut Rp 150.000,00 dan
keranjangnya hanya dapat
memuat 80 tangkai bunga, keuntungan
maksimum yang diperoleh pedagang
tersebut adalah ….
A. Rp 20.000,00
B. Rp 25.000,00
C. Rp 30.000,00
D. Rp 32.500,00
E. Rp 37.500,00
SEDANG
SUKAR

14. 4. Seorang ibu yang mempunyai 4 kg
terigu dan 2,4 kg mentega ingin
membuat donat dan roti untuk dijual.
Satu donat membutuhkan 80 gr terigu
dan 40 gr mentega, dan satu roti
membutuhkan 50 gr terigu dan 60 gr
mentega. Jika ia harus membuat paling
sedikit 10 buah donat. Maka model
matematika yang sesuai adalah …..
A. 8x + 5y ≥ 400; 2x + 3y ≥ 120; x ≥
10; y ≥ 0
B. 8x + 5y ≤ 400;2x + 3y ≤ 120;x ≥
10; y ≥ 0
C. 8x + 5y ≥ 400;2x + 3y ≥ 12;x ≥ 0; y
≥ 10
D. 5x + 8y ≥ 400;3x + 2y ≥ 12;x ≥ 0; y
≥ 10
E. 5x + 8y ≥ 400;3x + 2y ≤ 12;x ≥ 10;
y ≥ 0
5. Daerah yang diarsir pada gambar ialah
himpunan penyelesaian suatu sistem
pertidaksamaan linear.
SEDANG
SUKAR

15. Nilai maksimum dari f (x, y) = 7x + 6y
adalah....
A . 88
B. 94
C. 102
D. 106
E. 196
2.9 Menyelesaikan operasi
matriks.
Operasi dan
sifat matriks
15
1. Diketahui matriks : 








yxy
xyx
A
dan











32
2
1
1
y
x
B
Jika At = B, maka nilai x + 2y adalah
….
a. – 2
b. – 1
c. 0
d. 1
e. 2
MUDAH

16. 2. Nilai a yang memenuhi persamaan
matriks 





34
21








52
31
=






 c
ba
2
32
+ 





 44
2cb
adalah ....
a. – 3
b. – 2
c. –1
d. 3
e. 6
3. Diketahui persamaan matriks























516
20
12
14
25
45
y
x
.
Perbandingan nilai x dan y adalah ....
a. 3 : 1
b. 1 : 3
c. 2 : 1
d. 1 : 2
e. 1 : 1
4. Matriks X berordo 2 x 2 yang
memenuhi persamaan :
X
14
26






=
38
24







adalah ….
a.
1710
26








SEDANG
SEDANG
SEDANG

17. b.
1710
22








c.
12
102








d.
1710
248








e.
142
28








5. Diketahui matriks 







23
26
P ,









130
51
k
Q dan 






53
32
R .
Nilai k yang memenuhi persamaan
1
 RQP adalah ....
a. – 1
b.
3
1
c.
3
2
d. 1
e. 3
SEDANG
2.10 Menyelesaikan operasi aljabar
beberapa vektor dengan syarat
tertentu
Operasi dan
sifat vektor
16 1. Diberikan tiga buah vektor masing-
masing:
a = 6p i + 2p j − 8 k
b = −4 i + 8j + 10 k
c = − 2 i + 3 j − 5 k
Jika vektor a tegak lurus b, maka
vektor a − c adalah.....
MUDAH

18. A. − 58 i − 20 j − 3k
B. − 58 i − 23 j − 3k
C. − 62 i − 17 j − 3k
D. − 62 i − 20 j − 3k
E. − 62 i − 23 j − 3k
2. Diketahui titik A(3, 1, - 4), B(3, - 4, 6)
dan C(- 1, 5, 4). P membagi AB sehingga
AP:PB = 3:2. Maka vector yang mewakili
PC adalah…..
a. (
−4
3
−6
) b. (
4
−7
2
) c.
(
−4
3
6
) d. (
−4
7
2
) e. (
−4
−7
2
)
3. Diketahui vector a = kji  32
tegak lurus dengan kjixb 22  .
Nilai x yang memenuhi adalah....
a. 2 b. 5 c. 3
d. 6 e. 4
4. Deketahui vektor 𝑎⃗⃗⃗ =(
𝑝
2
−1
) , 𝑏⃗=(
4
−3
6
)
dan
𝑐 = (
2
−1
3
)
Jika a tegak lurus b maka nilai (a-
2b).(3c) adalah…
SUKAR
SEDANG
SEDANG

19. a. 171
b. 63
c. -63
d. -111
e. -171
5. Diketahui vektor a = 2t i - j + 3k, b = -
t i + 2 j - 5k, dan c = 3t i + tj + k. Jika
vektor (a + b) tegak lurus c, maka nilai
2t =....
A. − 2 atau 4/3
B. 2 atau 4/3
C. 2 atau − 4/3
D. 3 atau 2
E. −3 atau 2
SUKAR
2.11 Menyelesaikan masalah yang
berkaitan dengan besar sudut
atau nilai perbandingan
trigonometri sudut antara dua
vektor.
Sudut antara
dua vektor
17
2.12 Menyelesaikan masalah yang
berkaitan dengan panjang
proyeksi atau vektor proyeksi.
Proyeksi
vektor
orthogonal
18
2.13 Menentukan bayangan titik
atau kurva karena dua
transformasi atau lebih.
Komposisi
dua
Transformas
i
19
2.14 Menentukan penyelesaian
pertidaksamaan eksponen atau
logaritma.
Pertidaksam
aan
logaritma
20
2.15 Menyelesaikan masalah yang
berkaitan dengan fungsi
Fungsi
eksponen
21

20. eksponen atau fungsi
logaritma.
2.16 Menyelesaikan masalah deret
aritmetika.
Deret
Aritmetika
22
2.17 Menyelesaikan masalah deret
geometri
Deret
geometri tak
hingga
23
3 Menentukan
kedudukan, jarak
dan besar sudut
yang melibatkan
titik, garis, dan
bidang dalam
ruang.
3.1 Menghitung jarak dan sudut
antara dua objek (titik, garis
dan bidang) di ruang dimensi
tiga.
Jarak pada
bangun
ruang
24
Sudut pada
bangun
ruang
25
4 Menggunakan
perbandingan,
fungsi,
persamaan,
identitas dan rumus
trigonometri dalam
pemecahan
masalah.
4.1 Menyelesaikan masalah
geometri dengan menggunakan
aturan sinus atau kosinus.
Atururan
kosinus
26
4.2 Menyelesaikan persamaan
trigonometri.
Persamaan
trigonometri
27
4.3 Menyelesaikan masalah yang
berkaitan dengan nilai
perbandingan trigonometri
yang menggunakan rumus
jumlah dan selisih sinus,
Rumus
jumlah atau
selisih dua
sudut
28

21. kosinus dan tangen serta
jumlah dan selisih dua sudut.
5 Memahami konsep
limit, turunan dan
integral dari fungsi
aljabar dan fungsi
trigonometri, serta
mampu
menerapkannya
dalam pemecahan
masalah.
5.1 Menghitung nilai limit fungsi
aljabar dan fungsi
trigonometri.
Limit fungsi
aljabar dan
fungsi
trigonometri
29
30
5.2 Menyelesaikan soal aplikasi
turunan fungsi.
Soal
masalah
ekstrim
fungsi
31
5.3 Menentukan integral tak tentu
dan Integral tentu fungsi
aljabar dan fungsi trigonometri
Integral tak
tentu fungsi
aljabar
32
Integral
tentu fungsi
aljabar
33
Integral tak
tentu fungsi
trigonometri
34
Integral
tentu fungsi
trigonometri
35
5.4 Menghitung luas daerah dan
volume benda putar dengan
menggunakan integral.
Luas daerah 36
Volume
benda putar
37
6 Mengolah, 6.1 Menghitung ukuran pemusatan Ukuran 38

22. menyajikan dan
menafsirkan data,
serta mampu
memahami kaidah
pencacahan,
permutasi,
kombinasi, peluang
kejadian dan
mampu
menerapkannya
dalam pemecahan
masalah.
atau ukuran letak dari data
dalam bentuk tabel, diagram
atau grafik.
pemusatan
6.2 Menyelesaikan masalah sehari-
hari dengan menggunakan
kaidah pencacahan, permutasi
atau
kombinasi.
Aturan
perkalian
39
6.3 Menyelesaikan masalah yang
berkaitan dengan peluang
suatu kejadian.
Peluang
suatu
kejadian
40