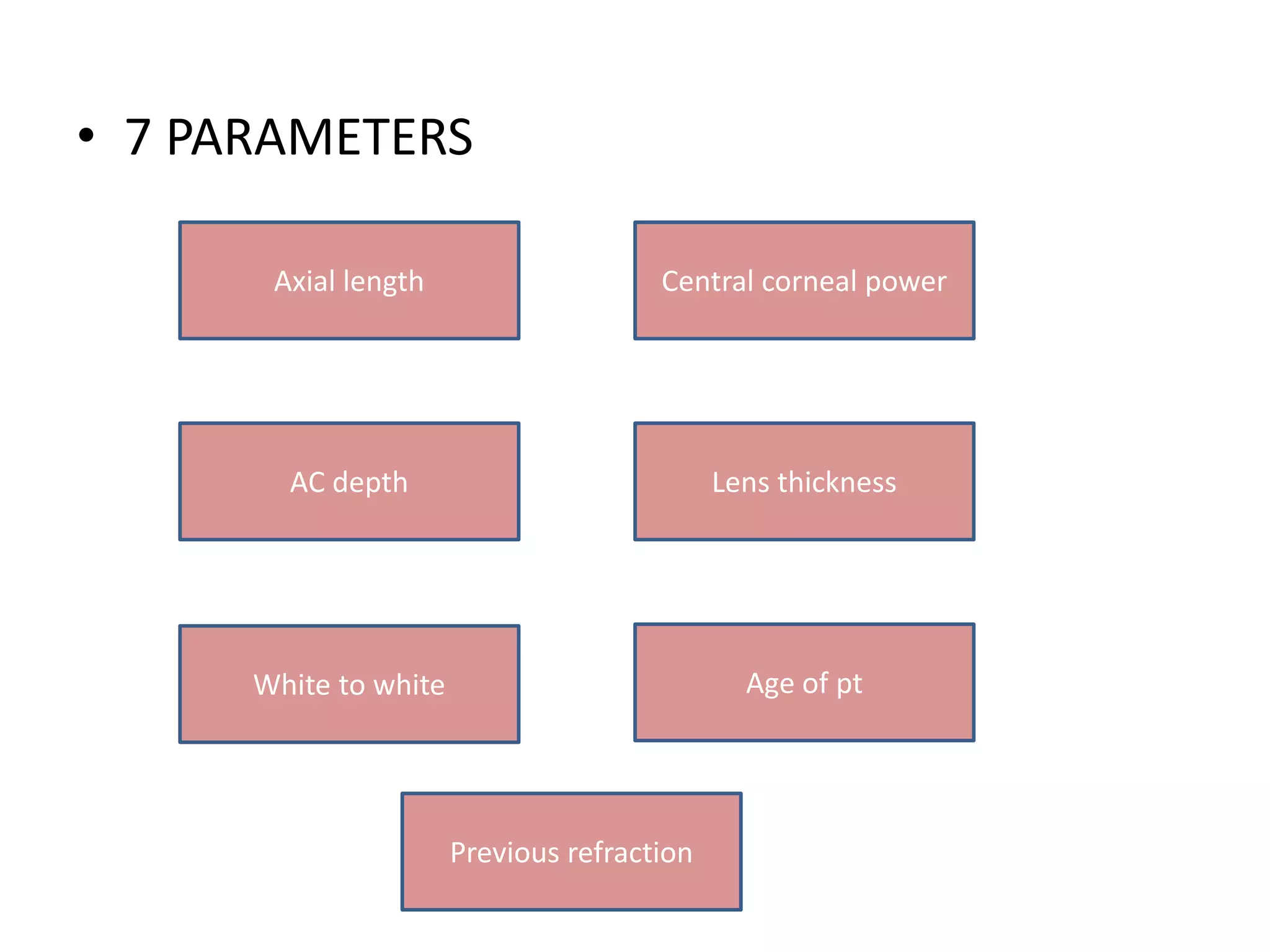
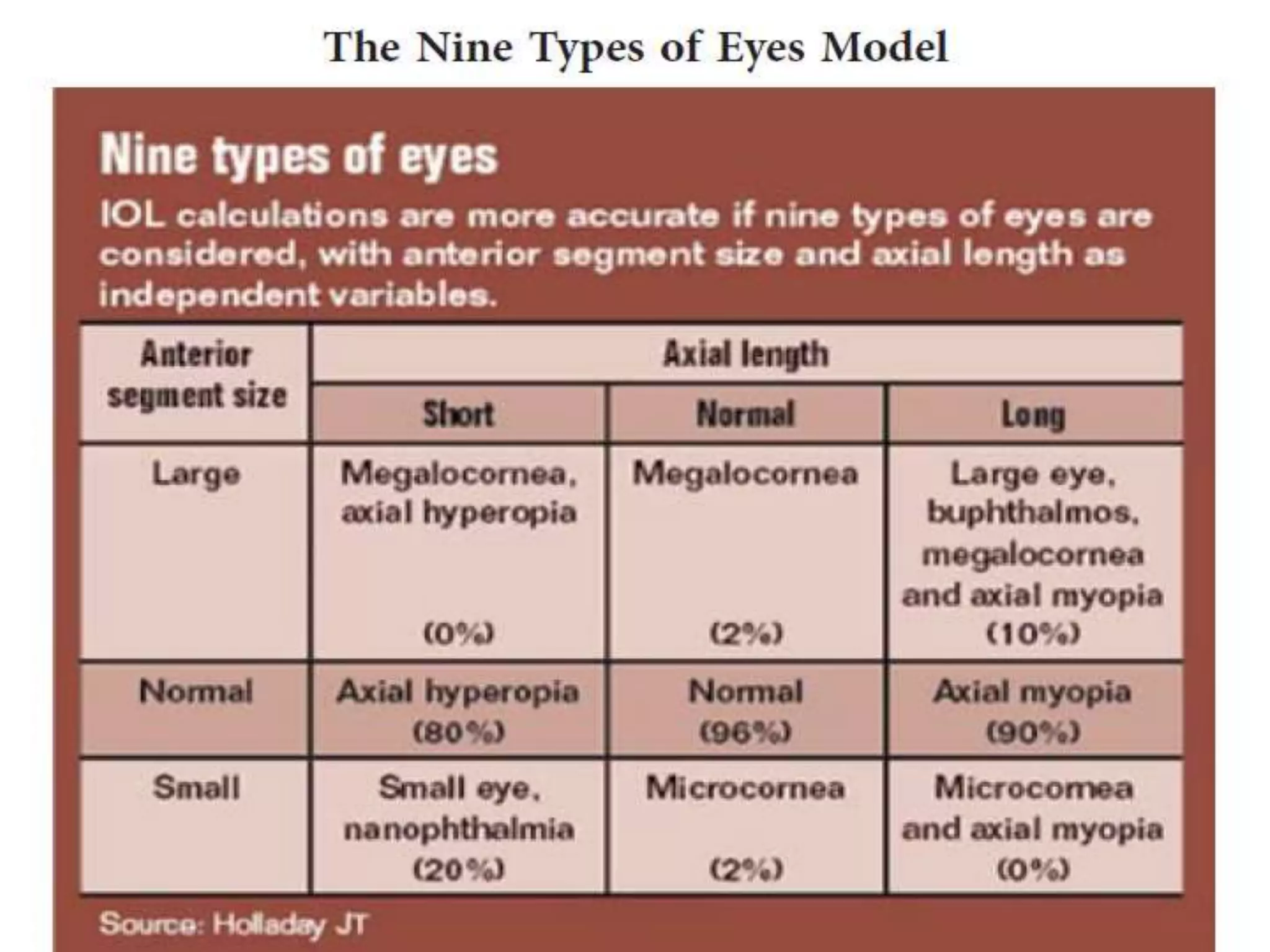
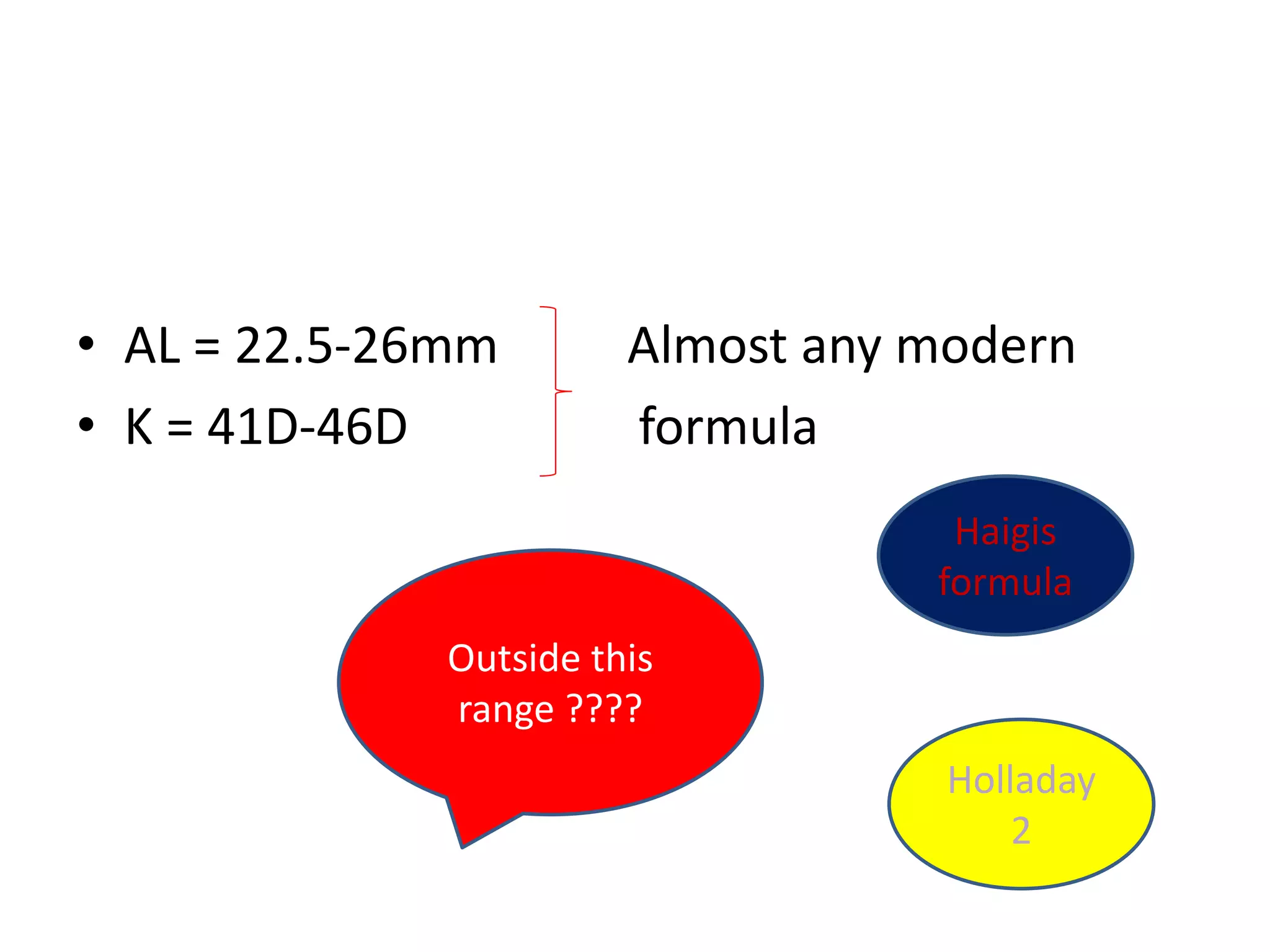
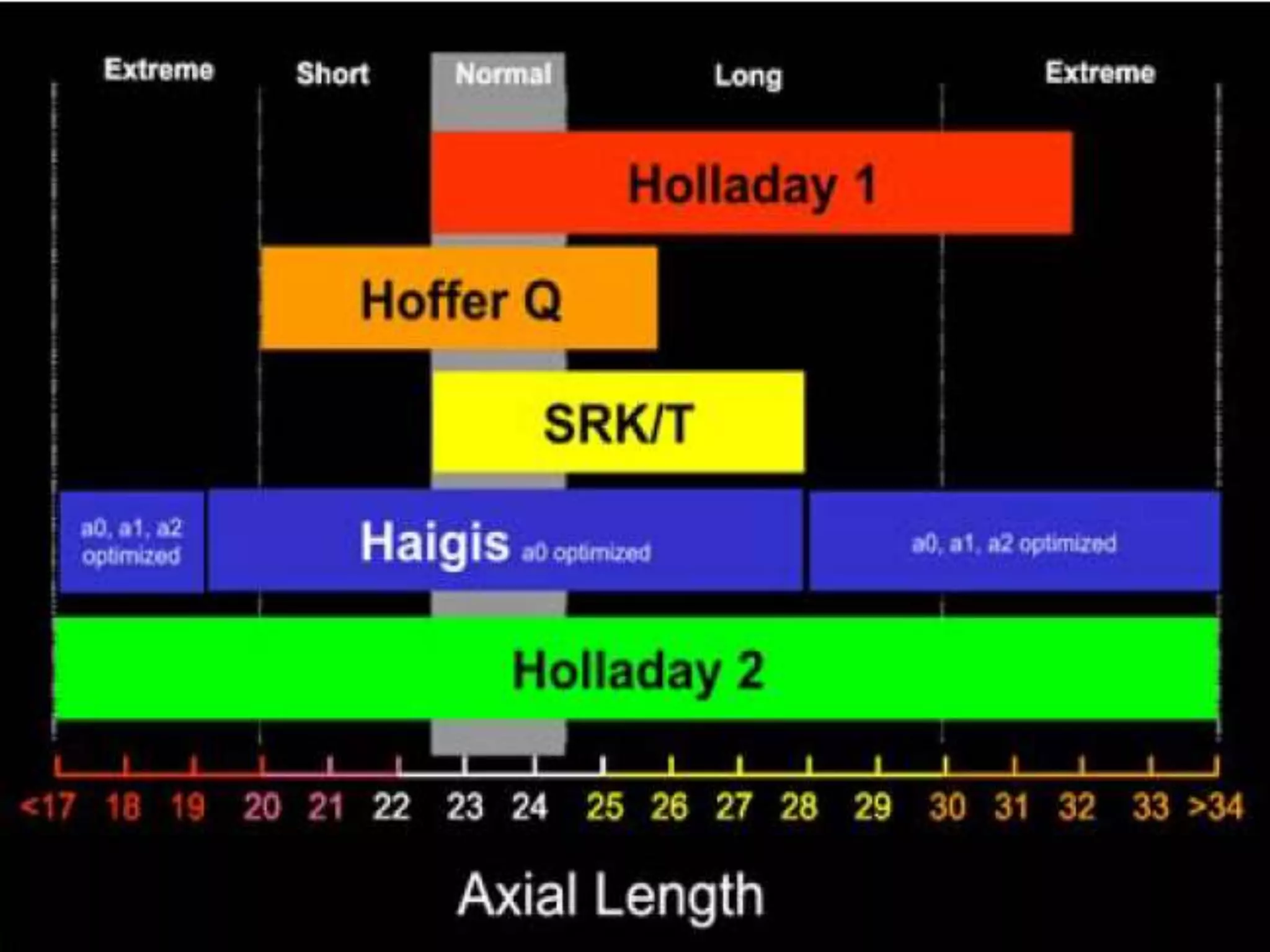
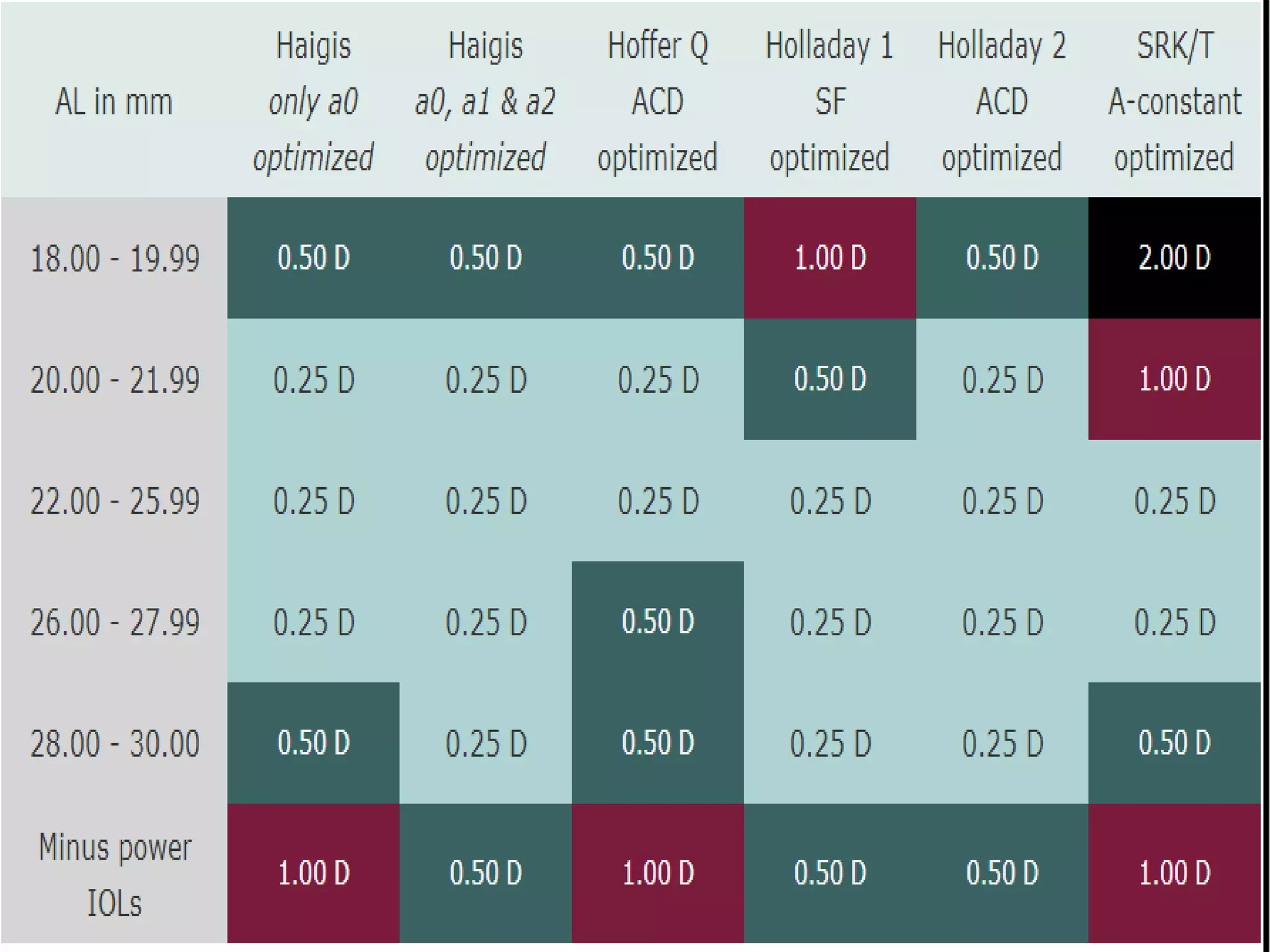
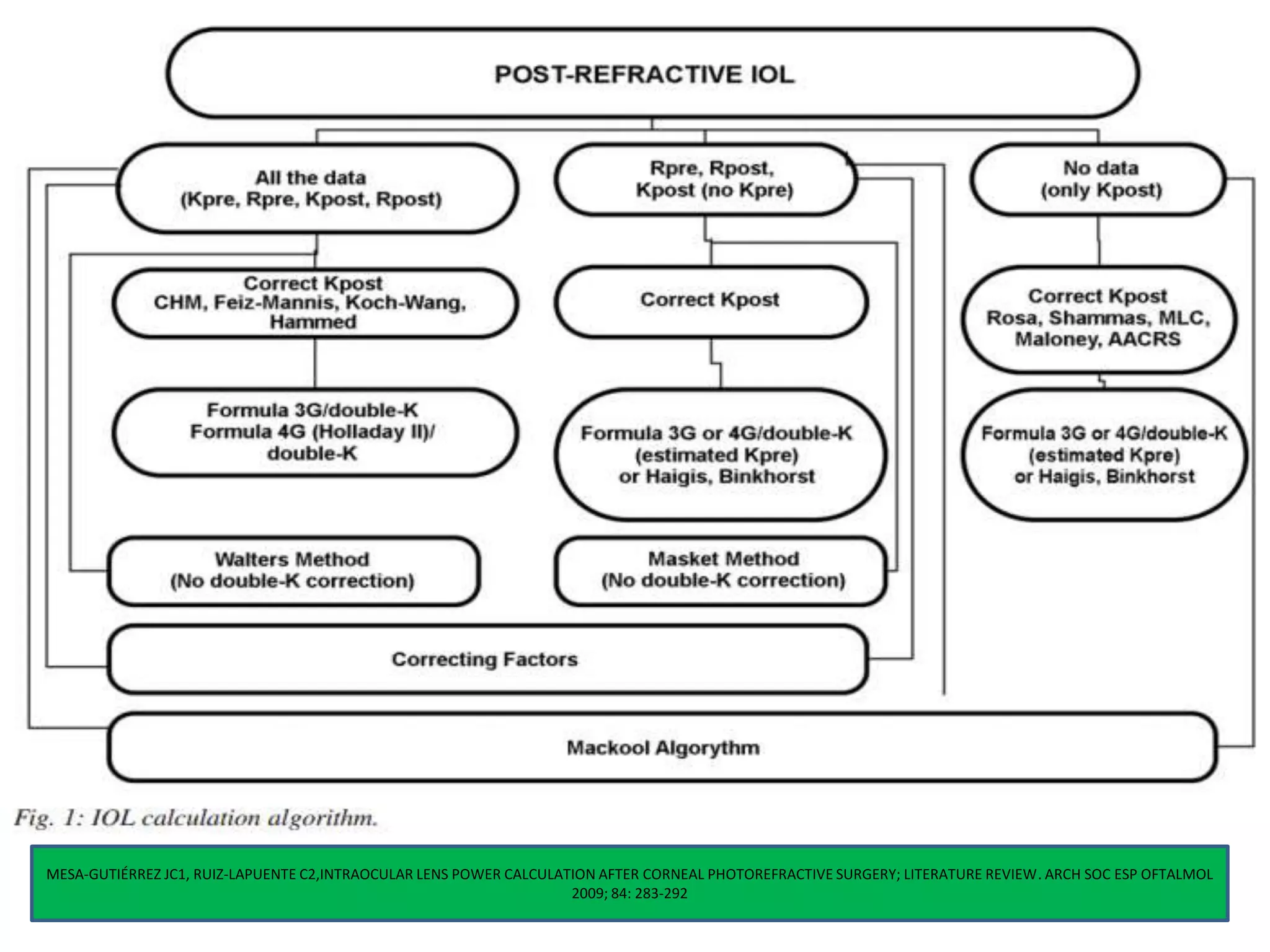
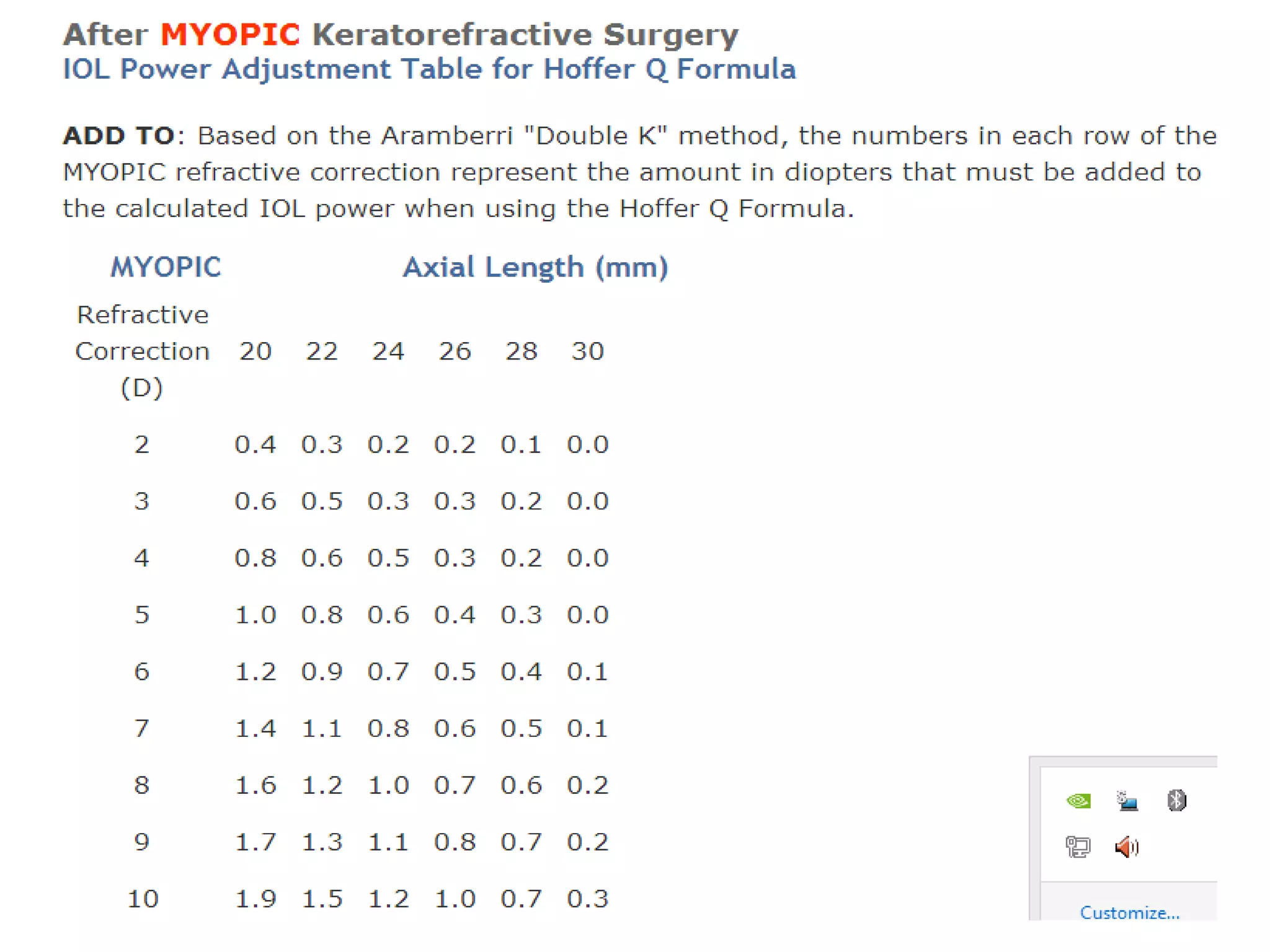
The document discusses various formulas used for calculating intraocular lens (IOL) power, including SRK, SRK2, Holladay, Haigis, and Holladay 2. It explains the factors these formulas account for such as axial length, corneal power, anterior chamber depth, and how they have evolved over generations to improve accuracy. Special considerations for calculating IOL power in cases involving prior refractive surgery, silicone oil filling, posterior staphyloma, and using optical biometry devices are also summarized.

1. IOL power calculation
FORMULAE

2. Generations!
• First – SRK 1 & Binkhorst formula
• Second – SRK2
• Third – SRK T , Hoffer Q , Holladay
• Fourth – Holladay 2 , Haigis

3. • Theoretical formulae – based on mathematical
principles revolving around the schematic eye
• Regression formulae – working backwards on
post operative outcomes
• 3rd and 4th generation – mix of both.

4. A closer look
1. SRK formula
• P = IOL Power
• K = avg central corneal power in Diopters
• L = axial length in mm.
P = A – 0.9K – 2.5L
Range - 22mm –
24.5mm

5. 2. SRK 2 formula – An attempt to
OPTIMIZATION
A1 =(A–0.5) for axial lengths greater than 24.5
A1 =A for axial lengths between 22 and 24.5
A1 =(A+1) for axial lengths between 21 and 22
A1 =(A+2) for axial lengths between 20 and 21
A1 =(A+3) for axial lengths less than 20

6. Why Optimize??

7. • All formulae work well within the range of
22.5-26 mm AL
• A constant computed based on
Avg AL 23.5mm
• Assumption
Reason??
AL α ACD
K α ACD
Dr Holladay

8. • SRK/T formula — uses "A-constant"
• Holladay 1 formula — uses "Surgeon Factor"
• Holladay 2 formula — uses "Anterior
Chamber Depth"
• Hoffer Q formula — uses "Pseudophakic
Anterior Chamber Depth"

9. • Hoffer-Q formula
• Dr Kenneth Hoffer – 1993
• P = f (A,K,Rx,pACD)
• A = AL
• K = avg corneal ref power
• Rx = previous refraction

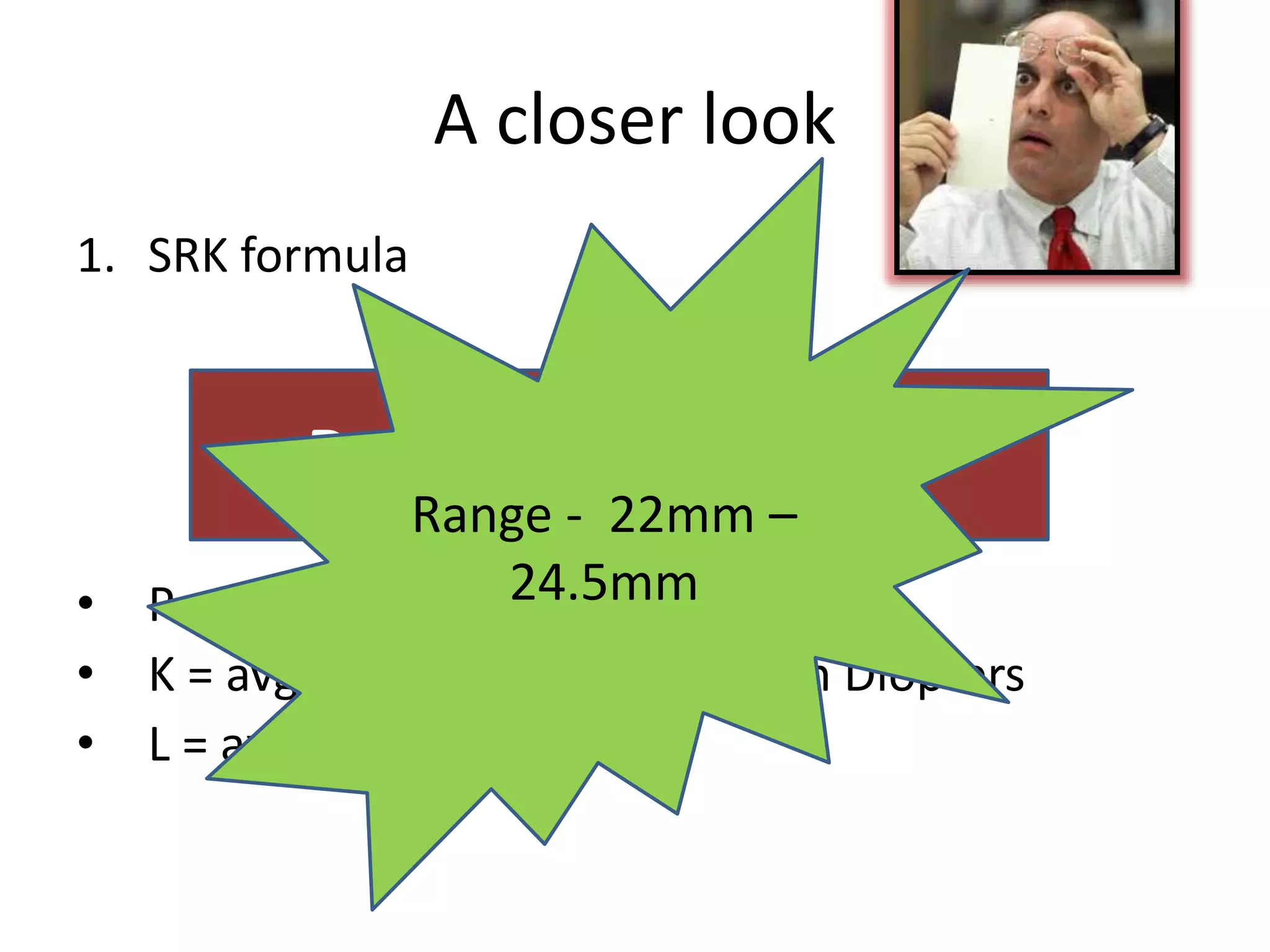
10. • pACD = The personalized ACD (pACD) is set
equal to the manufacturer's ACD-constant, if
the calculation was selected to be based on
the ACD-constant. In case the A-constant was
chosen, pACD is derived from the A-constant
[HOFFER, 1998] according to [HOLLADAY et al,
1988]
pACD = ACD-const = 0.58357 * A-const -
63.896 .

11. Haigis formula
• Gernet, Ostholt, Werner -1970 (GOW70 formula)
• D = a0 + a1 ACD+ a2 AL
• a0 constant moves the power prediction curve up
or down
• a1 constant is tied to the measured anterior
chamber depth
• a2 constant is tied to the measured axial length

12. Holladay 2
• Currently – most sophisticated formula
ACCURACY
PREDICTABILITY

13. 2 reasons for success

14. • 7 PARAMETERS
Axial length
White to white
AC depth
Previous refraction
Age of pt
Lens thickness
Central corneal power

16. Effective lens position
• Human eye – a dual lens system
In any dual lens system, if the
primary lens and the distance of
the screen are fixed, then the
effective power of the system will
depend on the power and position
of the second lens

17. Factors affecting ELPo
• Anatomical factors
1. K value
2. AL
3. Limbal white to white dist
4. Pre-op AC depth
5. Lens thickness
• IOL related factors
1. Shape
2. Length
3. Flexibility
4. Anterior angulation (if
any)
5. Material of haptic
6. Shape, design material
of optic

18. • Surgeon’s technique
1. CCC
2. Inadequate visco
removal
3. Capsular fibrosis
Bag to Sulcus shift

19. • AL = 22.5-26mm Almost any modern
• K = 41D-46D formula
Outside this
range ????
Haigis
formula
Holladay
2

22. Special cases

23. Post ref sx IOL calculation

24. • Require pre ref sx data
1. Clinical History method (manifest refraction, K
values)
2. Feiz–Mannis method (manifest refraction, K values)
3. Topographic method based on adjusting the
measured effective refractive power (EffRP)
(manifest refraction)

25. • Do not require
1. CL overrefraction (adjusting corneal power
using a correcting factor)
2. Orbscan topography
3. Maloney method

26. MESA-GUTIÉRREZ JC1, RUIZ-LAPUENTE C2,INTRAOCULAR LENS POWER CALCULATION AFTER CORNEAL PHOTOREFRACTIVE SURGERY; LITERATURE REVIEW. ARCH SOC ESP OFTALMOL
2009; 84: 283-292

27. Clinical history method
Postop K = (K before ref sx) –
(change in refraction at corneal
plane induced by the sx)
Corr-Kpost = Kpre - SEpre + SEpost
*SE = spherical equivalent

28. Feiz Mannis method
• Best used when good historical data is present
• Least likely to cause post op hyperopia
IOL pre – (∆D / 7) = IOL post where……
IOL pre = the power of IOL using pre LASIK
keratometry
∆D = the stable refractive change aftr LASIK at the
spectacle plane then…
IOL post = the estimated power of the IOL to be
implanted following LASIK

29. • It is helpful to keep in mind that the sign
convention for the change in refractive error
(ΔD) following myopic LASIK is a negative
number. Using the above formula, the new
calculated IOL power will always result in a
larger number.

30. The Koch-Wang Method
• We perform a corneal topography and take
the value of EffRp (effective refractive power).
Corr-Kpost = EffRp (ΔD x 0.19)

31. The Hammed Method
• We also take the EffRp value and calculate the
correction as follows:
Corr-Kpost = EffRPadj = EffRp-(ΔD/0.15)

32. The Shammas Formula
• Kpost(Shammas)=1.14 K-6.8.
• Kpost(Shammas)=1.14*44.25-6.8=50.45-6.8
• Kshammas=43.65D

33. The contact lens Method
• Subjective refraction → place rigid PMMA CL
→ refraction
• If refraction same…cornea has same power as
CL
• If refraction is myopic… CL has more power
than cornea
• Opposite in hypermetropia

34. The contact lens Method
Rpost=Refraction in post-op eyeglasses = -1D
Rlc= Correction with the contact lens = +1D.
Base Curve =CB=40
DR (Difference in Refraction)=Rlc-Rpost=+1-(-1)=+2
Corr-Kpost=CB+DR=39.25+2=41.25 D.

38. Silicon oil
• There are presently two viscosities of silicone oil in use:
• 1,000 mPa.s. silicone oil (Silikon, Alcon Laboratories, Ft. Worth, Texas)
slows sound waves to a little more than half the speed (980 m/sec) of
normal vitreous and can attenuate the returning sound wave during
ultrasonography so much that a good echoes are difficult, if not
impossible, to obtain.
• 5,000 mPa.s. silicone oil (ADATO SIL-ol 5000, Bausch & Lomb Surgical,
San Dimas, California) has a somewhat higher density, and slows
sound waves to approximately 1,040 m/sec. Typically, when
ultrasound measurements are made through silicone oil, hugely
erroneous axial lengths (such as 35 mm) are displayed.

39. • Without IOL master
• each component of the eye had to be
individually measured (usually at 1,532 m/sec)
and the true axial length calculated using the
velocity conversion equation
(TAL = Vc / Vm x AAL)
for the lens thickness and the vitreous cavity.

40. Holladay et al
Biconvex
IOL
PMMA plano
convex lens with
plano side
towards
vitreous…….over
an intact capsule
Silicone lens

41. • The additional power that must be added to the
original IOL calculation for a convex-plano IOL is
determined by the following relationship, as
described in 1995 by Patel and confirmed by
Meldrum:
• Ns = refractive index of silicone oil (1.4034).
• Nv = refractive index of vitreous (1.336).
• AL = axial length in mm.
• ACD = anterior chamber depth in mm.
• Additional IOL power (diopters) = ((Ns - Nv) / (AL -
ACD)) x 1,000

42. Average eye with silicon oil - +3 to
+3.5D

43. Posterior staphyloma
• 70% eyes with AL >33.5mm
• Pathological myopia
Difficulty in
obtaining posterior
retinal spike
????????
Posterior
staphyloma

44. • Anatomic AL ≠ refractive AL
• The simplest method
• Optical biometry using either the
1. Haag-Streit Lenstar or the
2. Zeiss IOL Master.
• If the patient's visual acuity is good enough, have him or her
look directly at the red fixation light, and the axial length
measurement will typically be to the center of the macula.